火焰原子吸收光度法测定水中铜的不确定度评定
吴松涛
(宜宾县环境监测站,四川 宜宾 644600)
不确定度是量值溯源的直接体现,是控制测量进程可能误差的度量,一切测量结果都不可避免具有不确定度,不确定度是表征合理地赋予被测量之值的分散性与测量结果相度量的参数。测量不确定度可由多个分量组成,当一个测量结果用于下一个测量时,其不确定度可作为下一个测量结果不确定度的分量,即它们是可传播的[1]。CNAS-CL01:2006和《检验检测机构资质认定评审准则》明确规定:检验检测机构应建立和保持应用评定测量不确定度的程序[2-3]。检验检测机构资质认定评审准则释义中还要求检测机构要有评定测量不确定度的案例。
1 试验方法及原理
1.1 试验方法及仪器设备
根据《水质 铜、锌、铅、镉的测定 火焰原子吸收分光光度法》(GB7475-87)的要求,用塞默飞科技有限公司的石墨炉火焰原子分光光度计(仪器型号:ICE 3300型;仪器编号:AA02125102)测定水中铜。
1.2 试验方法原理
将样品或消解处理过的样品直接吸入火焰,在火焰中形成的原子对特征电磁辐射产生吸收,将测得的样品吸光度和标准溶液的吸光度进行比较,确定样品中被测元素的浓度[4]。
2 试验步骤与数学模型的建立
铜含量是在波长324.8 nm的条件下,用0.5 nm通带,乙炔、空气为燃气,测定溶液吸光度Y。分别配制铜含量为0 mg/L、0.50 mg/L、1.00 mg/L、1.50 mg/L、2.50 mg/L、5.00 mg/L的系列标准溶液,平行测定3次,仪器采用最小二乘法对标准溶液浓度(X)和吸光度进行线性回归,建立方程:Y=a+bX。然后用铜质控样(200929),使硝酸酸度保持1%,用同样方法测定吸光度;水样中铜的浓度按式(1)计算:

式中:m——从校准曲线上查出或仪器直接读出铜含量,μg;V——试样体积,mL。
3 不确定度及不确定度分量的产生和评定
由试验步骤及建立的数学模型可看出:不确定度分量来自标准系列溶液的配置、溶液移取及定容过程、标准曲线拟合、铜质控样(编号:200929)的重复测定和仪器引入。产生的各不确定度分量是不相关的,因此,其合成不确定度可以按式(2)计算:

式 中:Uc—— 合成不确定度;Urel1,Urel2,
Urel3——不确定度分量1、2、3的相对标准不确定度。因此,要确定合成不确定度,应对火焰原子吸收光度法测定铜的所有步骤产生的不确定度分量进行评定。
3.1 标准贮备溶液产生的相对标准不确定度分量Urel11
标准贮备溶液是从环境保护部标准样品研究所购买的铜溶液,浓度为1 000 mg/L。从标准溶液证书上可知,其相对扩展不确定度为1.0%,k=2,标准溶液浓度定值服从正态分布,p=95%时,k=1.96,标准贮备溶液的相对标准不确定度:

3.2 标准中间溶液配制引起的相对标准不确定度分量Urel12
用5 mL天玻移液管(A级)移取标准贮备液于100 mL BOMEX容量瓶(A级)中,定容得到50 mg/L铜标准中间溶液。
3.2.1 溶液移取过程中引起的相对标准不确定度Urel12(V1)
用5 mL天玻移液管(A级)移取溶液,包括三部分不确定度。
第一是移液管体积的标准不确定度U1(v)。制造商提供的5 mL天玻移液管(A级)最大允许误差为±0.015 mL,假设服从矩形分布,标准不确定度为:

第二是充满液体至移液管刻度线的标准不确定度U2(v)。充满液体至移液管刻度的估计误差为±0.025 mL[5],按矩形分布换算成标准不确定度为:

第三是温度差异产生的标准不确定度U2(t)。因为校准是在20℃进行的,测定样品时假定实验室与校准温度相差5℃,钠钙玻璃体积膨胀系数是2.6×10-8℃-1,由校准温度不同而引起5 mL移液管(A级)体积变化为:

按矩形分布换算成标准不确定度为:

因此,溶液移取过程中引起的相对标准不确定度按式(2)计算可得:

3.2.2 100 mL容量瓶(A级)引起的相对标准不确定度Urel12(V2)
同样,100 mL容量瓶(A级)也包括三部分不确定度。
第一是容量瓶体积的标准不确定度U2(v1)。根据宜宾市计量测试所出具的检定证书,其最大允许误差是0.084 mL,计算标准不确定度为:

第二是充满液体至刻度线的标准不确定度U2(v2);充满液体至刻度线的估计误差是±0.08 mL,计算标准不确定度为:
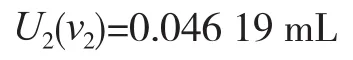
第三是温度差异产生的标准不确定度U2(t)。假设温差为5℃,则体积变化为:V=1.3×10-5mL
换算成标准不确定度为:

按式(2)计算,100 mL容量瓶(A级)引起的相对标准不确定度Urel12(V2)是:Urel12(V2)=6.698×10-4
由4.2.1和4.2.2按(2)式推算出配制标准中间溶液的相对标准不确定度分量:

3.3 标准系列溶液配制产生的相对标准不确定度分量Urel13
配制标准系列溶液需用5 mL移液管(A级)和100 mL容量瓶,因而其标准不确定度是由这两部分引入的。
3.3.1 5 mL移液管(A级)产生的相对标准不确定度Urel13(V1)
同理,5 mL移液管(A级)移取标准中间液,其不确定度也来源于移液管体积的标准不确定度:

液体充满移液管刻度线的标准不确定度:

测定样品时因温度不同而引起体积变化产生的标准不确定度为:

5 mL移液管(A级)产生的相对标准不确定度:

3.3.2 100 mL容量瓶(A级)产生的相对标准不确定度Urel13(V2)
100 mL容量瓶(A级)产生的相对标准不确定度Urel13(V2)计算过程同4.2.2,其结果为:

由4.3.1和4.3.2按式(2)得到标准系列溶液配制产生的相对标准不确定度分量:
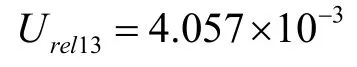
3.4 标准曲线拟合引入的相对标准不确定度Urel14
标准曲线拟合引入相对不确定度的计算方法很多,有计算标准曲线剩余标准差后,利用斜率、测试次数和测试试样的质量浓度测量值计算不确定度[6-8];也有根据拟合方程求各自的偏导数后,利用传播系数计算不确定度[7]。根据不确定度的定义,测量不确定度可以是测量结果的标准偏差(或其特定倍数),测量不确定度可以是包括概率的区间半宽度。火焰原子吸收光度法所配制的铜含量为:0.00 mg/L、0.50 mg/L、1.00 mg/L、1.50 mg/L、2.50 mg/L、5.00 mg/L的系列标准溶液,平行测定3次,测量数据如表1所示。

表1 标准曲线测定数据
由表1经最小二乘法计算得:截距a=1.02×10-3,斜率b=0.081,曲线相关系数r=0.999 8,即回归方程为:Y=0.081X+1.02×10-3。
标准曲线的剩余标准差SE是:

式中:SE——标准曲线剩余标准差;yi——仪器响应值;n——测量次数。
经计算SE=2.585×10-3mg/L,在95%的置信水平下,标准曲线仪器响应值的不确定度U为[9-10]。U=5.170×10-3mg/L,该不确定度是由引起的,=1.75 mg/L;所以,标准曲线拟合的相对标准不确定度是:

由式(4)可得,标准曲线拟合的相对标准不确定度为:

综上所述,配制标准溶液引起的相对标准不确定度的各个分量是不相关的,由(2)式得到配制标准溶液的相对不确定度为:

3.5 重复测定样品产生的相对不确定度Urel2
用铜质控样作为水样,需用10 mL移液管移取标准样品,用250 mL容量瓶定容;再用配制好的样品重复测定10次,计算测量样品产生的相对不确定度分量。
3.5.1 配制标准样品产生的相对标准不确定度Urel21
(1)10mL移液管(A级)产生的相对标准不确定度Urel15(V1)。10mL移液管(A级)移取标准样品,其不确定度也来源于以下方面。
移液管体积的标准不确定度为:

液体充满移液管刻度线的标准不确定度为:
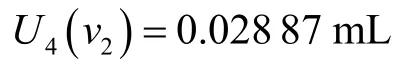
实验室与校准温差而引起移液管(A级)体积变化产生的标准不确定度为:
同理,10 mL移液管(A级)产生的相对标准不确定度为:

(2)250 mL容量瓶(A级)引起的相对标准不确定度Urel15(V2)。同样,250 mL容量瓶(A级)也包括三部分不确定度。
第一是容量瓶体积的标准不确定度:

第二是充满液体至刻度线的标准不确定度U5(v2)。充满液体至刻度线的估计误差按外推法算出是±0.5 mL,计算标准不确定度为:

第三是温度差异产生的标准不确定度:

所以,按式(2)计算,250 mL容量瓶(A级)引起的相对标准不确定度是:

由(1)、(2)按式(2)推算出配制质控样的相对标准不确定度分量是:

3.5.2 仪器重复测定标准样品产生的标准不确定度分量Urel22
将配制好的铜质控样直接吸入火焰原子分光光度计,重复测量10次,测量结果如表2所示。
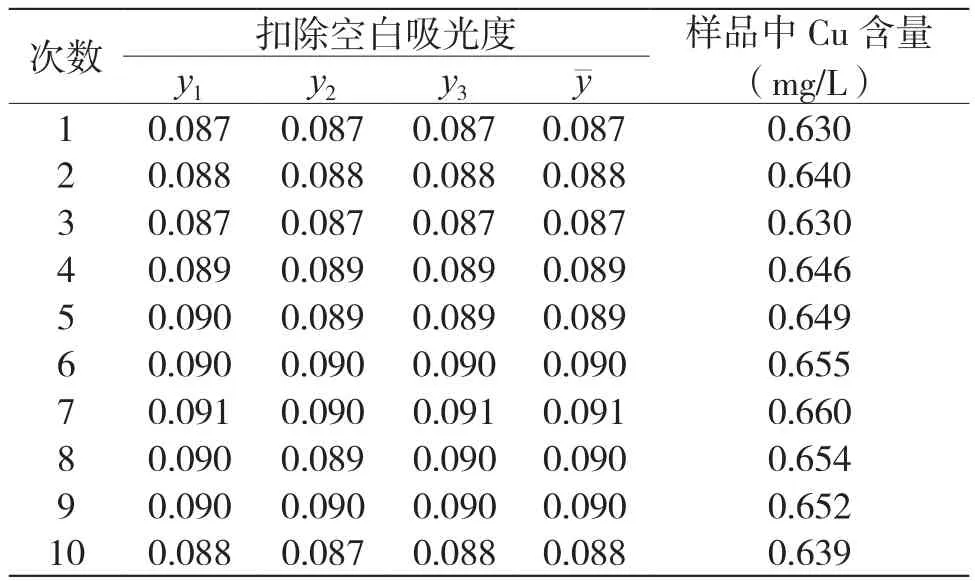
表2 质控样品重复性测量结果

式中:Urel22——样品测定的标准不确定度;yi——仪器测量样品响应值;——仪器测量样品响应均值;m——平行测量次数;n——重复测量次数。
由3.5.1和3.5.2按式(2)算出重复测定样品产生的相对不确定度:

3.6 仪器引入的相对不确定度Urel3
在火焰原子吸收光度计中,吸光度有一个末位数字的变化,其示值变化为±0.003,按均匀分布,标准不确定度为:1.732×10-3,样品重复测量10次,其=0.088 9,则其相对不确定度为:
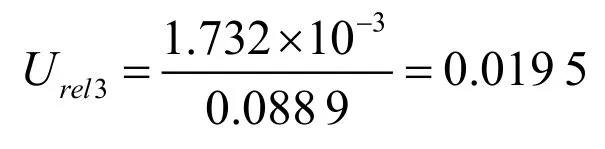
4 合成标准不确定度Uc
由:

因铜质控样是直接测量,则样品中铜浓度为:C均=0.646 mg/L,故合成标准不确定度为:

5 扩展不确定度
取包含量因子k=2,当p=95时,水中铜含量的测量是小子样,符合t分布,则U95为:

6 不确定度报告
由上面的计算,铜浓度C=0.646 mg/L,用扩展不确定度表示,测量结果为:
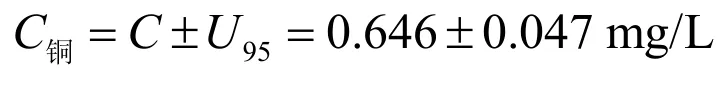
7 结语
火焰原子吸收分光光度法测定水中铜的不确定度来源于标准系列溶液配制过程、标准曲线拟合、仪器重复测定样品过程和仪器引入。其中,标准系列溶液配制、拟合过程和仪器引入是不确定度的主要来源,试验过程中应尽量提高仪器的灵敏度,控制标准溶液配制与拟合过程,做好玻璃器皿的校准和自校,尽量降低测量不确定度。
1 中华人民共和国国家质量监督检验检疫总局.JJF1059.1-2012 测量不确定度评定与表示[S].北京:中华书局,2013.
2 中国合格评定国家认可委员会.CNAS-CL01:2006 检测和校准试验室能力认可准则[S].北京:中国标准出版社,2006.
3 国家认证认可监督管理委员会.检验检测机构资质认定评审准则[S].北京:中国质检出版社,2016.
4 中华人民共和国国家环境保护局.GB 7475-87 水质 铜、锌、铅、镉的测定 原子吸收分光光度法[S].北京:中国标准出版社,1987.
5 中华人民共和国国家质量监督检验检疫总局.JJG 196-2006 常用玻璃量器检定规程[S].北京:中国标准出版社,2006.
6 许 伟,周 俊,周晓惠,等.还原-偶氮光度法测定废水中的硝基苯的不确定度评估[J].四川环境,2011,(1):46-47
7 周 娅,杨定清,谢永红,等.ICP-AES法测定土壤中铬含量的不确定度评定[J].四川环境,2012,(2):34-35
8 王 萍.连续流动分析仪测定水中氨氮的测量不确定度评定[J].四川环境,2012,(6):56-57
9 中国环境监测总站,环境水质监测质量手册编写组.环境水质监测质量保证手册[M].北京:化学工业出版社,1984.
10 北京农业机械化学院.应用数学[M].北京:北京农业出版社,1979.

