双索引机制的RDF数据图查询方法研究
郑志蕴,丁 阳,李 伦,李 钝
(郑州大学 信息工程学院,郑州 450001)
1 引 言
随着RDF1数据的增加,普通用户查询语义网数据的需求也在逐渐增加.通常RDF数据查询处理任务主要采用基于查询语言(比如RDQL、SPARQL等)的方法进行.其中SPARQL(simple protocol and RDF query language)2是 W3C 提出的 RDF 数据查询标准语言,也是被广泛采用的一种 RDF 查询语言.但是对于普通用户,这种形式化RDF数据查询方法的语法规则比较复杂,使用起来比较困难.因此从用户体验角度出发,关键词的检索方法是一种有效的查询机制,不仅能够保证查询的高效性,而且可以避免使用复杂的结构查询语言.
目前常用的关键词查询技术是将 RDF数据表示为一个带标签的有向图,图中的顶点对应三元组中的主语和宾语,谓词为边.使用图表示RDF数据既能保持数据间的关联信息又不丧失语义信息[1],因此RDF数据的查询处理通常被转化为图匹配问题,即在RDF数据图上定位包含关键词的斯坦纳树(Steiner Tree)[2],且主要分为两类.一类是将RDF数据转化为RDF图,该方法支持顶点的查询,但不支持边上的关联信息作为查询对象,因此为解决该问题提出了另一类方法,将RDF图转化为RDF二分图.该方法将边上信息进行封装作为RDF图的另一类顶点,在不破坏实体间关联关系的情况下,实现顶点和边的查询.然而转化后增加了图中顶点的个数使得关键词查询的存储空间增大,查询效率降低.因此如何在保证查找效率和存储空间的情况下,实现RDF顶点和边的查询成为一个重要的问题.
本文提出一种双索引机制的RDF数据图查询方法(QMRDI),支持顶点和边的查询.该方法首先将RDF数据建模为RDF数据图,然后将入度为0的顶点作为根节点,使用广度优先的方法对RDF图进行分割从而提高关键词的查找效率;其次根据邻接标签矩阵为每一个RDF子图构建一个顶点索引和边索引,利用字符串匹配的方法确定查询关键词所在子图的顶点索引和边索引的位置,通过两个索引的关系实现顶点和边的查询;最后利用相关性评测函数对查询结果子图进行相关性排序,输出top-k个查询结果子图.
2 相关工作
关键词查询方法主要分为两类,一类是将RDF数据转化为RDF图,支持顶点查询但不支持边查询;另一类是将RDF数据转化为RDF二分图,既支持顶点查询又支持边查询.
第一类的关键词查询可分为两种情况.
1)无索引结构[3-5].其中EASE[4]通过将RDF数据建模为RDF图,利用RDF图的邻接矩阵的N次方找到top-k个包含关键词的斯坦纳图作为查询结果子图.该方法的时间复杂度为O(n2)(n为RDF图中顶点的个数).然而,查询的响应时间会随着n的变大而变大,极大影响查询的效率.
2)引入索引结构[6,7].何昊等人提出的BLINKS[6]和SLINKS[6]方法以及司马强等人提出的模板树方法[7]等均是为了提高关键词查找效率而提前构建索引结构.其中最为经典是BLINKS[6]将数据图划分成不同的块,并为每一块构建一个块索引和块内索引.利用块索引查找关键顶点所在的子图,然后通过块内信息进行关键顶点的路径查询,最终将各个子图所得的路径进行合并得到查询结果.但是由于BLINKS采用为图中每一个顶点构建一个最短通路索引的方法,这样构建的索引不仅重复度比较高,并且不利于最终路径的查找.
第二类的关键词查询同样也可分为两类.
1)无索引结构[8].郑志蕴等人提出的KERBG[8]是一种基于二分图的RDF关键词扩展查询方法.该方法将RDF三元组中的谓词单独分开作为一类顶点,称为谓词顶点;RDF三元组中主体和客体作为另一类顶点,称为实体顶点.通过实体顶点到谓词顶点再到实体顶点的通路保持实体之间的关联.然后依据RDF二分图的反对称邻接矩阵及其幂矩阵,实现关键词查询的快速响应.但是随着RDF数据的增加,转化为二分图的时间也在增加.
2)引入索引结构[9].李慧颖等人提出的KREAG[9]是基于实体三元组关联图的RDF数据关键词查询方法.该方法将RDF数据建模为顶点带标签的实体三元组关联图,文本信息全部封装在关联图顶点标签上,不仅支持用户对关系进行查询,而且将RDF数据中实体间关联关系转化为关联图中顶点间的通路,有效保持了RDF数据的语义性.然而转化后的RDF二分图增加了图中顶点的个数,使得构建索引的长度增加从而影响索引的存储空间.
通过对上述方法的分析研究,提出双索引机制的RDF数据图查询方法,目的是在不需要转化为二分图的情况下,实现顶点和边的查询,同时提高关键词查询的效率,降低索引的存储空间.
3 相关定义
RDF数据是指以RDF三元组形式组织起来的语义信息,可以通过有向图模型表示.本文用(s,p,o)描述一个RDF三元组,并简记为t,用s(t)、p(t)和o(t)分别表示三元组中的主体、谓词和客体.下面给出RDF有向图的定义.
定义1(RDF有向图).设G=
图1是一个真实的RDF数据片段的RDF有向图表示,图中边上的标签存储了部分URI信息.
为了提高关键词查找效率,将给定的RDF图进行分割,此处采用文献[7]所给的方法,RDF图分割方法的定义如下.

图1 RDF图示例Fig.1 RDF graph
定义2(RDF图分割方法[7]).设G=
利用该方法对图1进行分割,分割后得到的子图如图2中(a)和(b)所示.

图2 RDF子图Fig.2 RDF subgraph
定义3(顶点索引和边索引).设Gr=
顶点索引(简称VI)是一个二元组VI=(VL,Lv),VL表示主体或者客体顶点的下标,从0开始计数;Lv表示顶点标签.
边索引(简称为EI)是一个三元组EI=(PL,Lp,PaL),PL表示谓词的下标,从0开始计数;Lp表示谓词标签;对于∀Vi,Vj∈V,p(t)∈E,若存在从Vi到Vj的关系序列Vip(t)Vj,则称Vi为p(t)的父节点,将其父节点的下标记为PaL,从0开始计数.若PaL=0,代表该谓词的父节点是根节点r.
图3给出的是图2(a)的顶点索引和边索引,其中实线箭头指向该顶点的父节点,虚线箭头指向该谓词的父节点.

图3 索引关系Fig.3 Index relation
下面以谓词year和顶点Breitbart为例说明两个索引的关系:
1)year的父节点的下标PaL(year)=2,说明year的父节点为顶点索引中下标为2的顶点,即Breitbart
2)Breitbart的下标为2,因此其父节点的下标PaL(Breitbart)=2-1=1,即Breitbart的父节点为边索引中下标为1的谓词,即author.
定义4(邻接标签矩阵).设G=
图4给出图2(a)的邻接标签矩阵.

图4 邻接标签矩阵Fig.4 Adjacency label matrix
给定RDF有向图G=
定义5(查询结果树).设与关键词K匹配的顶点的集合是M(K)={m1,m2…ms},查询结果定义为一棵满足下面条件的有向树:
1)G的树根是R;
2)对于每一个集合mi中的某个顶点vi,存在从R到vi的有向通路.
目前的方法[10-11]利用结果的紧凑性进行评分,此处采用[10]所给评分函数的定义.
定义6(评分函数[10]).设K={k1,k2…ks}的查询结果为RK,定义其评分函数为Score(RK)=Length(RK),其中Length(RK)为查询结果从树根到所有叶子节点的路径之和.
4 双索引查询方法
双索引查询方法主要由索引构建和关键词查询两部分构成.本节首先给出索引构造算法的描述,然后利用索引之间的关系设计关键词查询算法,并给出其算法的伪代码描述.
4.1 索引构造算法
为了提高关键词查找效率,首先为RDF图构建索引,其中索引包括顶点索引和谓词索引.下面是对索引算法的描述和完整的伪代码.
索引构造算法描述:
Step1.定义两个三维数组VertexIndex和EdgeIndex,其中VertexIndex存储每个子图的顶点位置和标签信息,EdgeIndex存储每个子图的谓词位置,标签信息及其父节点的位置.
Step2.将子图入度为0的顶点的下标VL(r)和标签信息Lv(r)存放在VertexIndex中,同时将VL(r)放入到队列LocationQueue中.若队列Queue!=null,根据定义4所得的邻接标签矩阵判断该顶点的相邻顶点,若当前邻接标签矩阵的值adjLabel!=null则将该谓词的下标,标签信息以及currentLocation的值存放到EdgeIndex中,同时将其相邻顶点的下标及其标签信息存放在VertexIndex.若当前邻接标签矩阵的值adjLabel=null说明该顶点不与当前顶点相邻,继续考察下一个顶点.
Step3.重复上面的步骤,直至队列为空为止.
结合上面对索引构造算法的具体描述,给出索引构造算法具体实现的伪代码描述.

算法1.索引构建算法Input:G=(V,E,L)isadatagraph;Kisasetofkeywordnodes;Output:EdgeIndexandVertexIndex1. LocationQueue<-anemptylocationqueue2. VertexIndex[Root][num][0]=VL(r)3. VertexIndex[Root][num][1]=Lv(r)4. LocationQueue.add(VL(r))5. whileLocationQueueisnotemptydo6. currentLocation=LocationQueue.poll()7. for(k=0;k 基于索引的关键词查询算法主要有关键词匹配、根节点的确定和查询结果的生成三部分.关键词匹配:使用字符串匹配方法确定查询关键词所在的位置.根节点的确定:查找一个可以到达所有关键顶点的根节点.最后将所得的候选结果,根据评分函数进行从低到高的排序,将前k个结果返回给用户.下面给出关键词查询算法的具体描述. 关键词查询算法: Step1.获取包含所有查询关键词的子图,给匹配的RDF子图中所有顶点和边定义一个存储到达输入关键顶点路径的数组v.path[k]. Step2.定义两个三维数组Vertex和Edge分别存放每个子图中与相应关键词匹配的顶点索引和边索引的位置,并用flag区分两类顶点,将Vertex和Edge中的所有元素放入队列Q中. Step3.依次遍历队列中的元素,输出该元素对应的路径p中的第一个元素,该元素是可以到达关键顶点的最新顶点的位置,最后一个元素是关键顶点的位置,分别记为first(p)和last(p),确定last(p)所对应的关键词,并将路径p存入v.path[k]中. Step4.判断first(p)所对应的顶点是否可以到达其余所有的关键顶点.若是,则将所有到达关键词的路径进行合并.否则,则根据first(p)的值以及定义3中所介绍的顶点索引和边索引的关系查找first(p)的父节点.若first(p)的标志位flag=0,说明与该关键词匹配的顶点属于顶点索引中的元素, 3http://lsdis.cs.uga.edu/Projects/SemDis/Swetodblp 则first(p)父节点的位置为PaL(first(p))=first(p)-1.若first(p)的标志位flag=1,说明与该关键词匹配的顶点属于边索引中的元素,则取出边索引中first(p)对应的父节点的位置PaL(first(p)). Step5.将PaL(first(p))添加到路径p中,并放入队列Q中.重复上面的步骤直至队列为空为止. Step6.使用评分函数对候选结果进行排序,返回前k个查询结果. 结合上面对关键词查询算法的具体描述,下面给出关键词查询算法具体实现的伪代码描述. 算法2.关键词查询算法Input:G=(V,E,L)isadatagraph;Kisasetofkeywordnodes;resultSetisasetofqueryresults;Output:answertoKBegin1. resultSet=null2. Q<-anemptyqueue3. forv∈V&k∈Kdo4. v.path[k]<-null5. endfor6. Q.insert(Vertex[Root][k][m])7. Q.insert(Edge[Root][k][m])8. whileQisnotemptydo9. p<-Q.remove()10. v<-first(p)11. if(forallk∈Kcorrespondingtolast(p))then12. v.path[k].add(p)13. endif14. if(forallk∈K,v.path[k]!=null)then15. result<-allpathswillbemergedfork16. if(!resultSet.contains(result))then17. resultSet.add(result)18. endif19. endif20. else21. if(first(p).flag=1)then22. PaL(first(p))=EdgeIndex[Root][first(p)][1]23. endif24. else25. if(first(p).flag=0)then26. PaL(first(p))=first(p)-127. endif28. Q.insert(PaL(first(p))->p)29. endwhile30. sorttheresultSetbyscorefunction31. returntop-kresults32. end 为了验证本文提出方法的性能,实验使用Java语言和MySQL数据库编程实现本文的查询方法QMRDI,在保证查询准确率的情况下与现有的BLINKS[6]和KREAG[9]方法进行对比. 实验环境配置如表1所示. 表1 实验环境 组件详细描述JDK版本1.7.0_03MyEclipse10.0OSWindows7sp132位CPUInteli3⁃21303.40GHz内存4G 实验采用真实的数据集swetodblp3,数据主题是计算机科学领域发表文章的信息.该数据中共包含681636个三元组,存储占用53.6MB,边数和顶点数分别为1026375和373219.其中入度为0的顶点的个数为16439,使用了637s完成对RDF数据集的分割. 本文在数据集上测试了两组共10个查询(表2),分别包含3-5个查询关键词.第一组Q1-Q5是不包含关系的测试查询.第二组Q6-Q10是包含关系的测试查询. 表2 查询示例 查询关键词Q1Breitbart 573 DatabaseQ2ADDS Modern Kim95Q31995 OQL[C++] 2002⁃01⁃03 QueryQ4Nathan DBMS Goodman95 ModernQ5Kelley Schema 621 kim95DatabaseQ6author ACFHK95 typeQ7Pages book_title relationQ8Author year 1995 ManagementQ9Kowalski E&P label last_modifiedQ10Rusin chapter_of kim95 type Book 图5分别显示了BLINKS,KREAG和本文所提方法QMRDI对表2中查询的响应时间.为了控制索引的存储空间,KREAG方法将索引的步长设置为8. 从图5中可得知,BLINKS的响应时间最长,原因是该方法需要在每个子图中基于块内索引和块间索引的双层搜索实现关键词的查询且所得查询结果可能并没有包含所有的关键顶点而造成无效查询,因此虽然结构图规模小于RDF图,但是其响应时间并不理想.KREAG方法需要遍历匹配的关键词索引中的每个记录,造成一些无效查询,影响了查询效果.BLINKS在第6-10的关键词查询时间相比于1-5的关键词查询时间有所下降,主要是因为该方法不支持关系查询,导致匹配的关键顶点下降,从而响应的时间偏低.而本文提出的方法QMRDI的响应时间最短,主要是因为首先确定包含所有关键词的子图,避免在没有包含所有关键词的子图中查询;其次提前为每个子图构建了顶点索引和边索引,并按照索引中记录的位置进行路径查找,不需要遍历索引中的每个记录,从而节约大量的时间. 图5 关键词查询响应时间Fig.5 Keywords query response time 图6分别显示了BLINKS,KREAG和QMRDI方法返回top-k个查询结果的查询响应时间,该查询响应时间为表2中10次查询的平均时间. 图6 top-k查询响应时间Fig.6 top-k query response time 从图6中可以看到,随着k值的增加各个方法的响应时间均在增加,而QMRDI响应时间的增长比较缓慢,主要是因为在同一个子图中可返回多个查询结果.KREAG的响应时间次之,根据匹配的关键顶点的最短通路索引进行路径查询时,k值越大则该方法需要查询的路径越长,造成无效查询越多,从而影响查询的时间.BLINKS的响应时间最长,随着k的增加需要返回的结果随之增加,该方法需要在更多的不同子图内进行路径的查询和合并,才能返回查询结果. 表3分别显示了BLINKS,KREAG和QMRDI方法所占存储空间大小,KREAG方法将索引的步长设置为8. 表3 索引空间 存储空间/MBBLINKS1216KREAG743QMRDI52 从表3中可知QMRDI所占空间最小,接近于整个RDF数据的存储空间,因为该方法只为每一个子图构建了一个顶点索引和谓词索引,因此实际上的存储空间就等于所有顶点(不包含重复的入度为0的顶点)和边的存储空间之和即O(V+E).KREAG是将RDF图转化为RDF二分图,因此顶点有三元组的个数和实体顶点的个数两部分构成,且为每一个顶点构建一个索引,因此索引所占的空间为O((VP+VE)2)(VP是三元组顶点的个数,VE是实体顶点的个数).BLINKS方法主要有块索引和块内索引两部分构成,同样采用为每一个顶点构建一个索引,因此其存储的空间为O(∑nb+BP)(其中nb代表该块内顶点的个数,B代表块的大小,P代表门户顶点的个数). 为了实现顶点和边的查询,本文提出双索引机制的RDF数据图查询方法.该方法首先将RDF数据建模为RDF数据图,然后对图进行分割;其次为每一个RDF子图构建一个顶点索引和边索引,利用两个索引的关系实现顶点和边的查询;最后利用相关性评测函数对查询结果子图进行相关性排序,输出top-k个查询结果.通过实验可知本文提出的方法在查询效率和存储空间上优于其它方法. [1] Du Fang,Chen Yue-guo,Du Xiao-yong,et al.Survey of RDF query processing techniques [J].Journal of Software(JSW),2013,24(6):1222-1242. [2] Zhang Yu,Jin Shun-fu,Liu Guo-hua,et al.Minimum steiner tree based method to keyword search[J].Journal of Chinese Computer Systems,2010,31(1):119-123. [3] Bhalotia G,Hulgeri A,Nakhe C,et al.Keyword searching and browsing in database using BANKS[C].Proceedings of the 18thInternational Conference on Data Engineering(ICDE),2002:431-440. [4] Li Guo-liang,Ooi B C,Feng Jian-hua,et al.Ease:an effective 3-in-1 keyword search method for unstructured,semi-structured and structured data[C].Proceedings of the ACM Conference on Management of Data(SIGMOD),2008:903-914. [5] Cui Yi-tong,Feng Zhi-yong,Wang Xin,et al.Research on large-scale RDF data query method based on graph clustering[J].Journal of Chinese Computer Systems,2015,36(12):2625-2628. [6] He Hao,Wang Hai-xun,Yang Jun,et al.BLINKS:ranked keyword searches on graphs [C].Proceedings of the ACM Conference on Management of Data(SIGMOD),2007:305-316. [7] Qiang Sima,Li Hui-ying.Keyword query approach over RDF data based on tree template[C].Proceedings of International Conference on Big Data Analysis(ICBDA),2016:1-6. [8] Zheng Zhi-yun,Wang Zheng-tao,Zhang Xing-jin,et al.KERBG:keyword expansion query approach over RDF data based on bipartite graph [J].Journal of Computer Science,2016,43(11):272-279. [9] Li Hui-ying,Qu Yu-zhong.KREAG:keyword query approach over RDF data based on entity-triple association graph[J].Journal of Computers(JCP),2011,34(5):825-835. [10] Tran T,Ladwig G.Index structures and Top-k join algorithms for native keyword search databases[C].Proceedings of the ACM International Conference on Information and Knowledge Management(CIKM),2011:1505-1514. [11] Li Jian-xin,Liu Cheng-fei,Zhou Rui,et al.Top-k keyword search over probabilistic XML data[C].Proceedings of the IEEE International Conference on Data Engineering(ICDE),2011:673-684. 附中文参考文献: [2] 张 宇,金顺福,刘国华,等.基于最小Steiner树的关键词查询方法[J].小型微型计算机系统,2010,31(1):119-123. [5] 催义童,冯志勇,王 鑫,等.基于图聚类算法的大规模RDF数据查询方法研究[J].小型微型计算机系统,2015,36(12):2625-2628. [9] 李慧颖,瞿裕忠.KREAG:基于实体三元组关联图的RDF数据关键词查询方法[J].计算机学报,2011,34(5):825-835.4.2 基于索引的关键词查询算法

5 实验与结果分析
5.1 实验环境及实验数据
Table 1 Experimental environment
Table 2 Query sample
5.2 查找效率
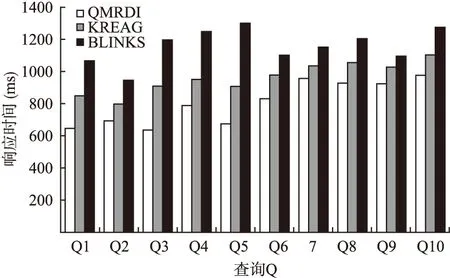

5.3 索引空间评估
Table 3 Index space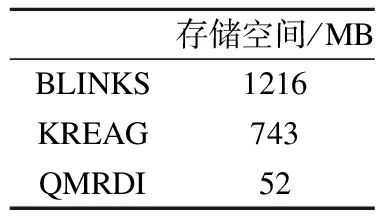
6 总 结
——论胡好对逻辑谓词的误读

