时序知识图谱的增量构建

张子辰，岳 昆，祁志卫，段 亮

云南大学 信息学院,昆明650500

近年来，知识图谱（knowledge graph，KG）作为结构化的语义知识库，用符号形式化的方式描述物理世界中的概念及其相互关系，成为了学界和业界的研究热点。KG 构建是知识图谱研究的关键，目前主要的构建方法先抽取非结构化数据中的实体和关系，然后以结构化的方式存储和表示实体与实体间的相互关系。然而，随着时间的推移，领域KG 的构建需要实时反映新的知识，例如，新知识可能来源于各种社交媒体中快速产生且不断演化的数据，需要将其不断添加到KG 中，进而反映随时间推移知识库的演化发展。因此，如何高效地将数据中蕴含的新知识添加到当前KG 中，完成时序KG 的增量构建，具有重要意义。上述开放世界背景下数据驱动的时序KG 增量构建，可以丰富现有KG 并实时地反映知识的演化更新，仍存在如下挑战：

（1）由于数据中蕴含的新知识需要不断更新到当前KG 中，而KG 作为一种高维、复杂的图结构，需要一种能够高效描述时序KG 并支持其增量构建的模型。

（2）添加合适的新知识，是完成时序KG 增量构建的关键，需要一种能够度量新知识与当前KG 吻合程度的方法，作为评判能否添加的依据。

针对挑战（1），现有的图嵌入法大多通过TransE、TransH和TransD等基于知识表示的翻译模型，将高维、复杂、异构的KG 嵌入到低维、统一、稠密的向量空间中，进而完成对现有KG 的构建和知识表示。另外，基于翻译模型还衍生出许多其他表示学习模型，如TransH 在TransE 基础上设计出新的翻译模型TransAH，提高了训练学习的效率和知识表达能力。文献[11]提出一种改进的知识表示模型STransH，采用单层神经网络的非线性操作来加强实体和关系的语义联系，获得了更优的效果，可用于大规模知识图谱构建和推理等任务。但是，这些构建方法只针对现有KG 进行构建，对随时序产生的新知识如何进行增量构建，仍有待进一步探索。

为了描述KG 中知识随时间变化的相应更新，Goel 和Wang 等基于静态KG 的嵌入模型对多关系事件构建时序KG。由于事件具有时效性，为了弥补在事件和时间关系方面覆盖范围和完整性方面的不足，文献[14]融合了事件的时间信息，通过神经网络对事件的上下文信息进行编码，从而构建时序KG。Gottschalk 等基于时序KG 的特点构建了多语言、以事件为中心的时序知识图谱EventKG。但是，上述构建方法主要针对现有事件的时序信息来构建KG，而如何将外部数据所蕴含的新知识不断添加到KG 有待进一步探索。

对此，本文提出了一种数据驱动的时序KG 构建方法，实现时序KG 的增量构建。具体而言，给出时序KG 的定义，并基于TransH 提出了一种时序KG 建模方法，从而获得时序KG 的嵌入向量。为了保证KG 嵌入到低维向量空间的损失最小，利用随机梯度下降法（stochastic gradient descent，SGD），从而使增量构建的模型损失最小。

针对挑战（2），目前大多数方法通过对KG 中实体间的关系或三元组中缺失的实体进行补全，即知识图谱补全（knowledge graph completion，KGC）。其中，一些封闭世界下的KGC 方法，不考虑新增的实体关系，如基于路径和规则预测实体间的新关系和基于元学习预测实体关系，使KG 更加完整。学者们还考虑到新增的外部知识，即开放世界下的KGC，如Socher 等提出了基于张量神经网络（neural tensor network，NTN）的模型，用以推断实体间的关系，通过训练KG 中的三元组来抽取真实文本中实体间的关系，并补充到KG中。Shi等提出了ConMask模型，用于学习实体名称的嵌入和部分文本描述，进而将外部实体连接到KG 上。上述方法主要针对三元组中的缺失实体或关系进行补全，而面对数据中所包含的大量且完整的新知识（即新三元组集合），仍有待进一步探索。

因此，本文的增量构建方法将把基于数据获得的新知识（新三元组）添加到当前KG 中，进而完成KG 的增量构建。例如，一条少数民族新闻报道了“卡雀哇”节日，从中抽取出新的三元组如“（独龙族，节日，卡雀哇）”、“（马库村，紧邻，中缅边境线）”和“（卡雀哇，活动，剽牛祭天）”等。可以看出三元组“（独龙族，节日，卡雀哇）”与独龙族相关，可将其增量更新到KG 中，过程如图1 所示。

根据图1 实例中新增三元组与当前KG 的关系，考虑以下两个问题：（1）如何只添加与当前KG 有关的新知识。如实体“卡雀哇”与当前KG 中的“独龙族”存在新的“节日”关系，而“马库村”没有这一关系，因此“（马库村，紧邻，中缅边境线）”应该去除。（2）如何把与当前KG 间接关联的三元组添加到KG中。如三元组“（独龙族，节日，卡雀哇）”与当前KG相关联，而“（卡雀哇，活动，剽牛祭天）”没有这种关联关系，但这两个三元组之间相关，因此“（卡雀哇，活动，剽牛祭天）”也应添加到当前KG 中。

图1 KG 添加新三元组实例Fig.1 Example of adding new triple to KG

为了直观度量新三元组与当前KG 的吻合程度，本文采用激活函数将其转化为一个权值，用此度量新三元组与当前KG 的最终吻合度。然后，为了添加与当前KG 具有间接关联的新三元组，本文基于贪心策略提出了最优子集的提取算法，将最优新三元组集合添加到当前KG 中，完成时序KG 的增量构建。

最后，通过建立在Wikidata、CN-DBpedia 和Freebase 数据集上的实验，与现有的KGC 方法进行比较，验证了本文方法的高效性和有效性。

1 时序知识图谱的增量构建

1.1 时序知识图谱定义

时序KG 是由不同时刻下KG 组成的序列，把初始时刻的KG 记为，随着时间的推移，增量变化如下：

其中，G(0 ≤≤)表示时刻的KG。

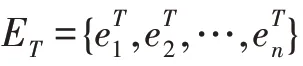
随着时间推移，将数据中蕴含且符合G的新知识增量构建到G中，得到G，同时将新的实体关系添加到E和R中，进而得到E和R。该过程可表示为：

其中，Δ表示这个时段所产生的新知识，即新三元组集合。

1.2 增量构建

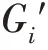
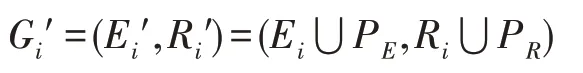
其中，P为集合中所有三元组包含实体的集合，P为集合中所有三元组包含关系的集合。

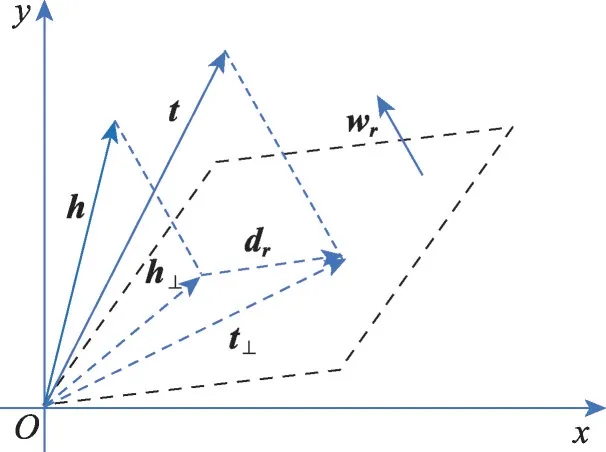
图2 实体与关系向量空间Fig.2 Vector space of entity and relation

然后，将向量转化到超平面上（记为d），那么嵌入带来的损失表示为：

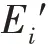
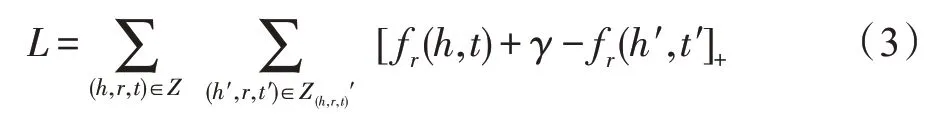
其中，为三元组集合，即正样本集合；′是构造的负样本三元组集合；[·]是一个正值函数。

为了使构建数据集较大时的损失最小，并提高构建效率，利用随机梯度下降算法来获取最小值。具体而言，每次随机抽取出个正样本（记为），然后为中每个三元组构造一个负样本，再把这些正样本和负样本合并为一个集合（记为）。随着梯度的下降，不断迭代更新向量位置，从而得到损失最小的G的表示模型。上述思想见算法1。

从G构建G

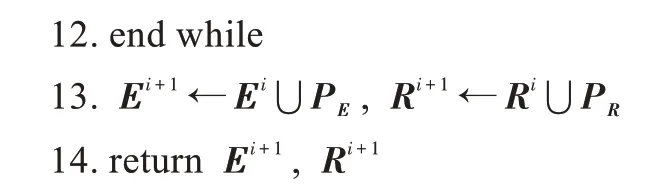
随机梯度下降计算过程中，每次选取个正样本以及构造个负样本，则采样计算损失需要次。假设梯度下降迭代步数为次，即while 循环执行次，因此该算法的时间复杂度为(·)。

2 新三元组与当前KG 的吻合度计算

2.1 吻合度计算

为了保证时刻所添加的知识与G相吻合，本节提出吻合度计算模型，用于度量三元组与当前KG 的吻合程度。首先，从时刻所产生的新知识中抽取出三元组集合Δ，然后将Δ嵌入到G的向量空间中，并且从两方面来度量吻合度：（1）模型吻合度，即三元组是否能够与G的增量构建模型相吻合；（2）语义吻合度，即三元组能否与G的语义信息相吻合。

模型吻合度：由于G是通过时序KG 增量构建模型得到的，基于式（2）计算出(,,)∈Δ与G的模型吻合度：

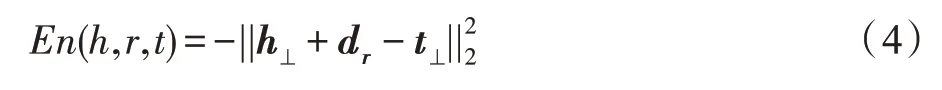
其中，表示时刻，(,,)越接近0，吻合度越高。

语义吻合度：由于G中关系的数量远远小于实体的数量，分别计算每个实体∈E与(,,)∈Δ中、的余弦相似度，即度量其与G上节点的相似度及相似度的最大值，如式（5）所示：

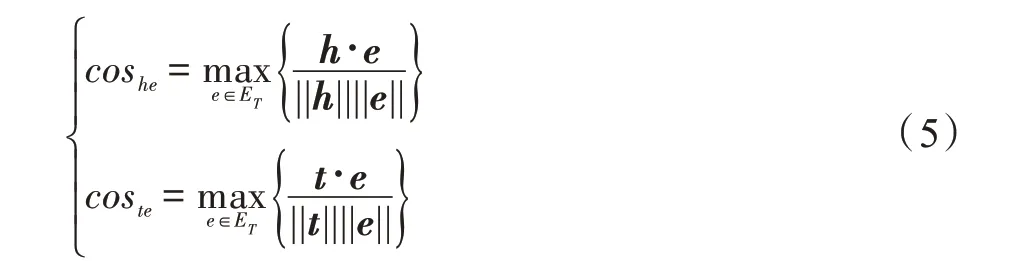
在任意三元组(,,)中，若或与当前KG 中某个实体相似，则说明该实体与G的语义信息相吻合。具体而言，比较cos和cos，把其中较大值作为该三元组与G的语义吻合度，方法如下：

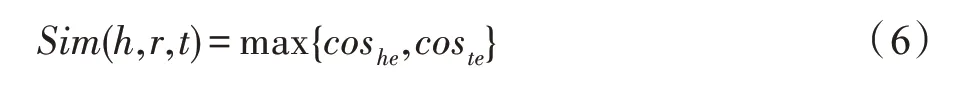
其中，若或与E中有相同的实体，则该三元组为目标三元组。

为了得到该三元组与G的吻合程度，用激活函数把两个因素构造出一个特征向量，用来表征每个三元组的特点：

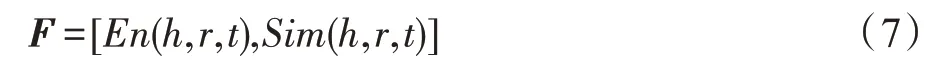
然后利用式（8）的激活函数将特征向量转化为权值(,,)∈[0,1]，将其作为评判三元组与当前KG 的吻合度的依据。

其中，是一个非线性激活函数，和表示在训练时可以调节的参数矩阵。(,,)越接近1，表明该三元组与G的吻合度越高。

2.2 提取最优三元组集合

不难发现，(,,)很小的三元组也可能与当前KG 中的知识相关。例如，待添加的三元组“（独龙族，节日，卡雀哇）”和“（卡雀哇，活动，剽牛祭天）”，前者权值较高，但后者较低。若只设置阈值，后者可能不会添加到KG 中。因此，不仅要提取权值较大的三元组，还要找到那些权值不高但与当前KG 间接关联的三元组，进而获取集合Δ的最优子集和最大权值，即最终的目标函数。对此，本文提出基于贪心策略的提取最优子集合算法，使子集用最少的三元组来表征集合Δ。由于KG 中实体数往往大于关系数，把最优子集和Δ中的所有实体分别记为P和Δ，给出约束条件P≈Δ，使集合表征集合Δ。该问题描述如下：

其中，表示最优子集的最大权值。

对此，先找到集合Δ中权值大于阈值的三元组，将其添加到集合中，并更新集合P、权值，再从Δ中去除它。此外，为了找到那些权值不高但可以添加的三元组，先找到能够与集合中任一三元组相连接的其他三元组放入一个候选集合，进而从中选择权值最大者并添加到中。直至找不到能够连接的其他三元组（即=∅），返回最优子集和权值。具体步骤如算法2 所示。

提取最优子集

算法2 中，假设集合Δ包含个三元组，那么for 循环需要执行次。若候选集中有N个元素，则第二个while 循环的时间复杂度为(·N)。最坏情况下算法的时间复杂度为(·N)。

算法2 执行到第(1 ≤≤)步时，选择的个三元组包含在最优解子集中。

令集合Δ为={,,…,s}。当=1 时，选择集合中权值最大的元素。显然，它是最优解子集中一个元素。否则，将这个权值最大的元素添加到中则会出现实体重叠，因此让其与产生实体重叠的元素替换，可以得到一个更好的最优解，矛盾。假设前(1 ＜≤)步选择的元素是最优解的一部分，则在进行第+1 步时，与其相连的元素中权值最大的元素一定包含在最优解中。否则，将该元素放入中会出现实体重叠，因此把产生实体重叠的元素替换为该元素，可以得到一个更好的最优解，矛盾。推广到前步依然成立，则定理成立。

通过定理可知，算法2 的输出为最优解，则通过最优子集合就能增量构建得到G，进而随着时间推移，不断提取最优三元组集合，从而实现时序KG 的增量构建。

3 实验结果

3.1 数据集

为了模拟时序KG 的增量构建过程，将Wikidata（http://dumps.wikimedia.org/wikidatawiki/entities）、CNDBpedia（http://www.openkg.cn/dataset/cndbpedia）、Freebase（https://developers.google.com/freebase）作为测试数据集，并按照其发布时间来划分三元组添加的顺序。通过实验测试本文提出的时序KG 增量构建方法的效率及有效性，同时与典型的KGC 方法进行实体预测结果比较。上述数据集中所包含的实体、关系和三元组个数的统计信息如表1 所示。

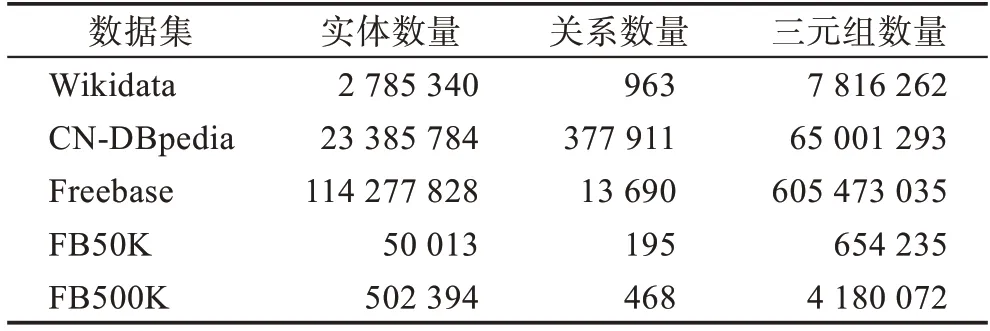
表1 数据集Table 1 Datasets

3.2 效率测试

与+1 时刻的数据集对应的KG 记为G，前一时刻的KG 记为G。使用本文方法，将从时刻到+1 时刻新增的三元组作为集合增量地构建至G中，进而得到G。

首先，针对添加不同数量集的三元组集合（新知识），在同一数据集下测试其执行时间，如图3 所示：（1）增量计算的时间，即完成三元组吻合度计算和得到最优子集合的执行时间；（2）构建时间，即算法1 的执行时间。可以看出，在不同数据集下，随着数量集的增加，执行时间也大幅上升，特别是在Freebase 下的平均增量构建时间约是Wikidata 下的13 倍。另外，对于不同数据集中添加相同数量的三元组，数据集越大，增量构建时间越长，在CN-DBpedia 与Wikidata 中共同添加10个三元组，前者的执行时间接近后者的两倍。

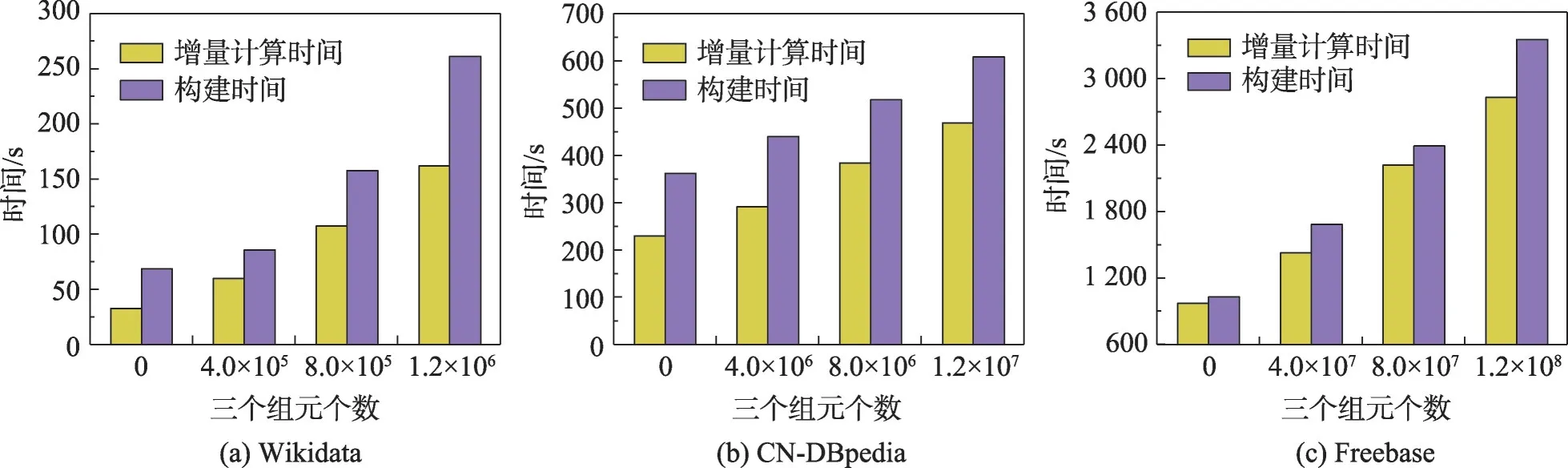
图3 不同数据集下的Gi 增量构建时间Fig.3 Execution time of incremental construction of Gi with different datasets

然后，测试了算法1 不同迭代次数、不同数据集情形下的构建时间，如图4 所示。可以看出，模型构建时间随着迭代次数增加而增加，其中三元组过亿的Freebase 迭代1 000 次的时间相较于100 次增加了接近1.3 倍。

图4 不同迭代次数下Gi+1 的构建时间Fig.4 Execution time of Gi+1 construction under different iteration times

3.3 有效性测试

为了验证吻合度度量模型以及增量构建算法的有效性，使用准确率(Precision，)、召回率(Recall，)和1 值来评价提取结果，三个指标的计算方法如下：其中，为提取出能够添加到G中的三元组个数；为能被检索到的三元组个数，即进入过候选集的三元组个数；为所有需要添加的三元组个数。

首先，测试了算法2 中阈值对提取结果的影响，如图5 所示。可以看出，随着阈值的减小，准确率、召回率和1 值都有所上升。特别地，在数据集CN-DBpedia 中，当阈值从0.8 到0.7 时三个指标的上升幅度最大，都接近0.15。这是因为CN-DBpedia 中有一些孤立三元组且权值小于0.8，导致提取数量骤增，当阈值不超过0.7 时，结果较为稳定。

图5 不同阈值下的提取结果Fig.5 Extraction results under different thresholds

另外，从Freebase 数据集中提取一定数量的三元组，记为FB50K。在该数据集下，与一些现有的KGC方法进行抽取效果的对比，测试了阈值的改变对提取结果的影响，如图6 所示。

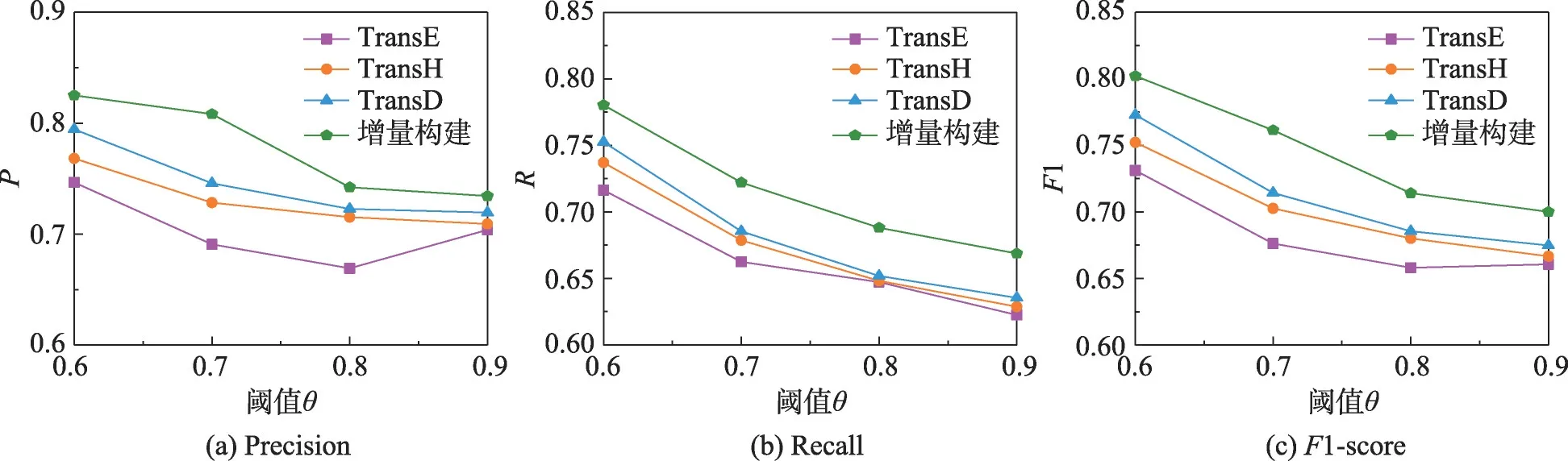
图6 不同方法的提取结果Fig.6 Extraction results of different methods

可以看出，本文提出的增量构建方法的准确率、召回率和1 值均高于其他KGC 方法，尤其是在阈值为0.7 时，本文方法的准确率提升了0.06 以上，这是因为算法2 能够顾及一些权值较低但与当前KG 相符的三元组，而其他KGC 方法无法提取出这些三元组。同时随着阈值的上升，虽然提取到符合的三元组数量有所下降，但本文方法的三个指标仍然高于其他方法。

接着对Δ进行划分，其中一部分三元组是与G相关联，记作Δ={(,,)|∈E或∈E}；另一部分则与G无关联，记作Δ={(,,)|∉E且∉E}，把Δ在Δ的占比记为(0 ≤≤1) 。然后，在不同数据集下测试了占比对提取结果的影响，如图7 所示。可以看出，随着无关三元组的减少，提取效果越来越好。从占比0.8 到0.5，其准确率大幅提升了接近0.3。

图7 不同占比下的提取结果Fig.7 Extraction results under different proportions

为了得到尽可能好的数据提取结果，将阈值设为0.7，占比设为0.5，在同一数据集下测试提取结果的有效性，如表2 所示。可以看出，随着新增三元组数量的增加，增量构建结果的准确性也有所上升。同时，也统计了不同数据集下G的增量构建后三元组、实体和关系新增的数量，如表3 所示。总之，若当前KG 与所添加的新知识相关度较高，则提取效果更好，可更好地丰富当前KG。

表2 不同数据集下的提取结果Table 2 Extraction results under different datasets

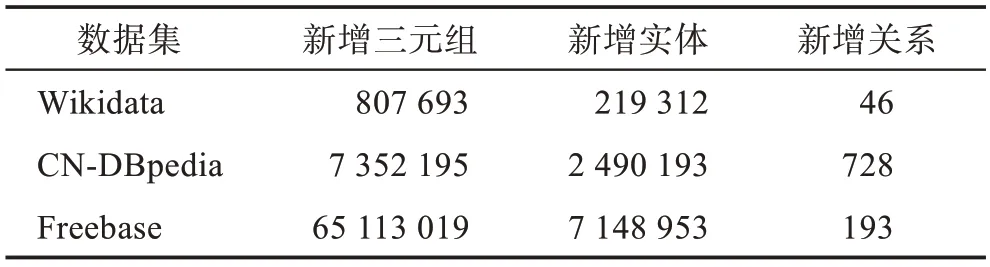
表3 不同数据集下的增量构建结果Table 3 Results of incremental construction under different datasets

3.4 实体预测

为了验证本文方法对于KGC 任务的有效性，再从Freebase 数据集中提取一定数量的三元组，记为FB500K。在FB50K和该数据集下，与其他方法进行实体预测并对比预测结果。基于TransE、TransH和TransD算法，把新知识直接嵌入到模型中训练，进而完成预测，分别记为TransE(OW)、TransH(OW)和TransD(OW)。

针对不同数据集，用平均排序（mean rank，MR）和HITS@50 来评价预测结果的有效性，MR 值越低，HITS@50 值越高，则说明结果更加准确，结果如表4所示。可以看出，本文方法的实体预测结果较好，因为其能够过滤新知识中的部分无关信息（孤立三元组），使实体总数目相对于TransE(OW)较少，进而MR和HITS@50值较好。

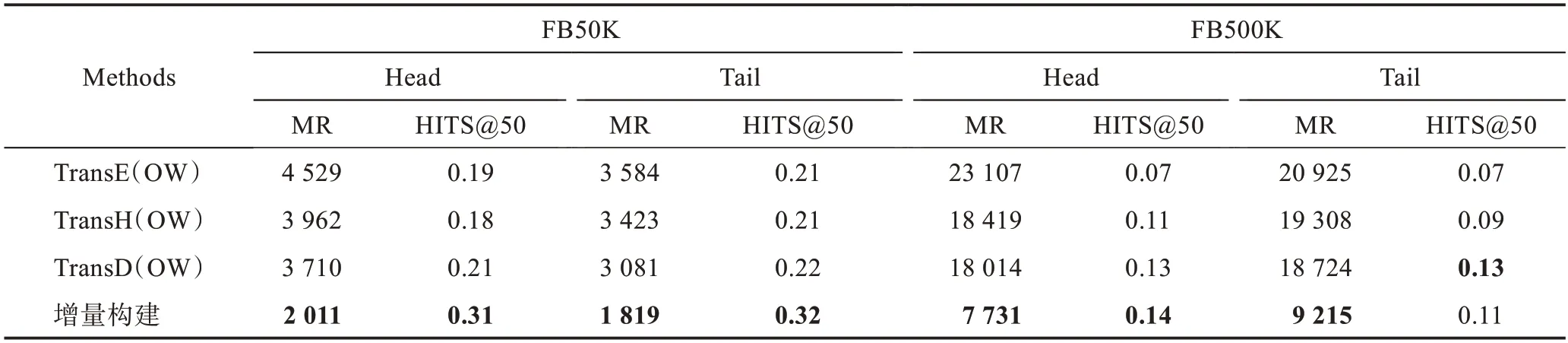
表4 开放世界下实体预测结果Table 4 Open-world entity prediction results

然后，也在封闭世界下与其他KGC 方法进行实体预测，结果如表5 所示。可以看出，时序KG 增量构建方法整体优于其他方法。这是因为算法2 不仅能够把权值较大的三元组添加进去，还能把自身权值较低，但与权值较大的三元组有关联的三元组添加进去，使补全的结果较为全面。总体而言，相比开放世界和封闭世界下的KGC 方法，本文方法对于实体预测都具有一定优势，验证了本文方法的有效性。

表5 封闭世界下实体预测结果Table 5 Closed-world entity prediction results

4 结束语

本文提出了时序KG 的增量构建方法，通过构建吻合度计算模型和提取最优子集算法获得最优三元组集合，并将该集合增量构建到KG 中。实验结果表明，本文方法能够有效地提取出较为吻合的三元组并增量构建到KG 中，但是在实体预测任务中存在对TransH 模型的依赖，导致预测结果不够理想。因此，未来工作将考虑实体关系间的其他特征，更好地表征当前KG，进而改善增量构建模型，提升新知识增量构建的准确率。另外，拟将本文方法拓展到真实场景下，基于数据中蕴含的新知识对领域KG 进行增量构建。