覆盖模型的传感器网络寿命问题建模及其求解
赵海军,贺春林,蒲 斌,陈毅红
1.西华师范大学 计算机学院,四川 南充637009
2.物联网感知与大数据分析南充市重点实验室,四川 南充637009
目前,无线传感器网络中的能量优化极为重要,因为与传统的Ad-hoc 网络相比,它们在功耗、计算能力和存储容量方面都受到一定限制。因此,无线传感器网络中的最优化能量消耗已成为最重要的性能指标。
传感器节点一般只能配备有限的电源/电池(本文称为初始能量供给)。在某些应用场合,电源的补给是不可能的。正如文献[1]所指出,电池的能量密度每5~20 年仅增加1 倍,这表明能量管理是传感器网络的关键。
传感器网络中传感器节点的主要任务是监控事件,即收集数据和快速执行本地数据汇聚,然后传送数据。因此,能量消耗体现在三方面:感知、数据汇聚和通信。数据汇聚的能量实际上不受监测调度的影响,对于文献[6]提出的分布式自组织调度来说,没有考虑相关的能量损失和增加的通信开销。文献[7]提出了一种用网格数据结构来表示一个区域上的传感器节点覆盖,构成一个×阵列来分割区域,然后为每个点确定出覆盖传感器圆盘形的子集。在这种模型中,如果网格点较少,则要覆盖的区域就不好确定,如果网格非常精细,则计算开销就相当大,因此这种模型很难适合实际的传感器网络覆盖。文献[8-9]把网络覆盖问题简化为不相交集覆盖问题,即假设任何传感器不能参与其他不同的传感器覆盖,这样,每个传感器只能从休眠模式转换为活跃模式才能覆盖相应的区域,从而造成覆盖孔洞和能量的巨大消耗。文献[10]针对栅格统计法的不足,提出了一种基于圆弧并面积的几何覆盖率算法。这种算法尽管提高了覆盖率,但没有对参与覆盖的传感器节点的能量消耗和通信开销加以考虑,在传感器数量较大且并发传输的情况下可能造成网络中断。文献[11]基于网格点的区域覆盖算法未考虑网络的固有特征,导致算法存在近似及复杂度偏高等问题,提出了基于改进的粒子群算法和特征点集优化的区域覆盖算法。这种算法一方面仅考虑了传感器网络的区域最佳覆盖,而未对整个网络的覆盖寿命加以考虑,另一方面则是着重于减少覆盖算法的复杂度,因此不太适合实际应用。文献[12]针对有向传感器网络全覆盖问题,基于有向传感器节点概率感知模型提出了一种有向传感器节点部署结构,并引入标准工作方向的概念,使用奈曼-皮尔森准则数据融合方式,以最少的传感器节点实现目标区域全覆盖。但这种覆盖感知模型需要传感器节点强大的数据处理能力和通信能力,从而造成网络大量的能量消耗,进而缩短传感器网络的寿命,同时也增加了网络部署的成本。文献[13]提出了一种定向功率管理技术操作系统来提高传感器节点的能量效率,但是这种技术的复杂性造成了覆盖部署的难度和可操作性。文献[14-15]的模型假设无线传感器网络的大多数能量消耗来自于寻由的流量,而不是监测,从而减少网络生存寿命。
基于现有算法关于传感器网络寿命问题(sensor network life problem,SNLP)研究的侧重点不同以及存在的某些不足,本文提出了一种新的传感器网络覆盖模型及其数据结构,并在此基础上把SNLP 等效为它的对偶问题——最小权值传感器覆盖问题;然后把SNLP 构建为一个包装的线性规划,分别提出了求解它的集中式算法和分布式算法。仿真实验结果表明,本文提出的基于传感器网络覆盖模型和数据结构的SNLP 及其求解算法,能够使得模型和求解算法在质量、可扩展性和灵活性方面表现出较好的优势。
1 传感器网络覆盖模型及其数据结构
1.1 传感器网络的建模
为了研究传感器网络的寿命问题,首先对要研究的传感器网络进行建模。假设传感器部署在需要监测的区域上,且每个传感器p有它自己的监测区域(或称覆盖区域)R,即p无需借助于任何其他传感器,可以收集来自R的可信数据。还假设每个传感器p具有一定的初始能量供给b,由于能量消耗可以与时间消耗对应起来,即一个传感器的初始能量越大,可以消耗的时间就越长,因此也可把能量用时间来度量(为简便起见,本文的时间一律是指归一化单位时间)。同时还假设实际部署的传感器数量超过监测区域所需要的传感器数量,这样才有可能把一些传感器置于空闲模式,以节省它们的能量来延长网络寿命,传感器可以多次切换它们的模式。主要的限制条件就是监测区域(或指定的部分区域)必须完全在任何时刻被活跃的传感器覆盖。目标就是使感知能量消耗最小化,从而使得传感器网络寿命最大化。
首先给出能量保存调度问题的形式化定义。
把一组覆盖的传感器集合称为传感器覆盖,则一个监测调度就是(,),(,),…,(C,t) 的对集合,这里C是一个传感器覆盖,t是C有效的覆盖时间。
传感器网络寿命问题(SNLP):
给定一个监测区域,一组传感器,,…,p和每个传感器p的监测区域R以及初始能量供给b,寻找一个具有最大时间长度++…+t的监测调度(,),(,),…,(C,t),其中=1,2,…,,以使对于任意传感器p来说,总的活跃时间不超过b。
图1 给出了一个实例来说明多模式交换的优势。实例中有3 个传感器,各自具有圆盘形的监测区域、和,任意两个传感器都可以覆盖监测区域,但任意单个传感器都不能覆盖。
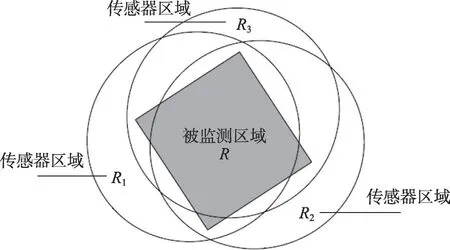
图1 3 个具有圆盘形监测区域传感器监测方形区域Fig.1 Three sensors with disc monitored regions monitoring square region
假设它们监测内部的一个方形暗区,每个传感器有2 个时间单位的初始能量供给,只存在一个不相交的传感器覆盖,它可以持续2 个时间单位;显然,调度({,},1),({,},1),({,},1) 是可行的且持续3个时间单位。
为了求解SNLP,需要找到可行的传感器覆盖,即把求解SNLP 的问题变成求解它的对偶问题——最小权值传感器覆盖问题。可以把这个对偶问题表述为:
给定一个监测区域,一组传感器,,…,p和对于任意传感器p的监测区域R以及权值w,寻找具有最小总权值的传感器覆盖。
1.2 传感器覆盖的数据结构
把监测区域用一个平面图形=(,)来表示,其中顶点集对应于全部传感器覆盖区域(如圆盘形)的边界的交叉连接点,边集连接沿着传感器圆的边界的相邻交叉点的对点。如图2 所示,平面图形=(,)有10 个顶点,21 个边和13 个面。
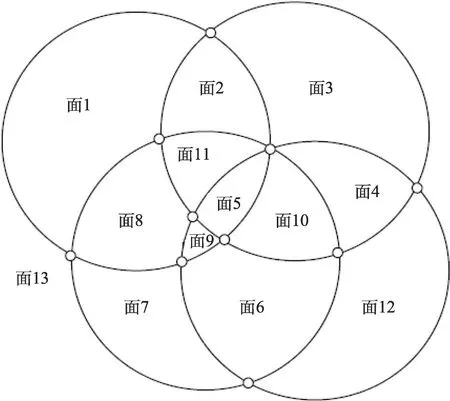
图2 具有圆盘形监测区域的4 个传感器的数据结构Fig.2 Data structure for 4 sensors with disc monitored regions
可以看出,图的面即是通过边使分割后的有限个平面部分。如果一个面的至少一个内部点被一个传感器覆盖,那么整个面就被相同的传感器所覆盖,因此必须高效地找到所有的面。
令为全部传感器的监测区域的边界交叉点的数目,则图中的面数目最多为+2。
证明基于平面图形的欧拉公式。因为=(,)是一个平面图形,故||-||+||=2,其中、和分别是的顶点集、边集和面集。如果几个边界线相交在同一点上,那么通过稍微改变边界线,就可以增加面的数目。因此,为了计数起见,可以假定每个点可以是至多两个监测区域的边界线的交叉点,则图的每个顶点有4 个度。如果把全部顶点的度加起来,则计算每个边2 次,因此||=2||,这样,||-2||+||=2,且面的数目等于||=||+2=+2。
如果监测区域是凸的,则任意两个边界可以最多相交2 次,也就是说,至多有(-1)个交叉点。
给定个传感器,每个传感器具有凸的监测区域,则图的面数目至多为(-1)+2。
显然,只要找到传感器覆盖区域的全部交叉点,就能在()的时间内高效地找到全部的面。
2 SNLP 的集中式求解
为了采用集中式算法求解SNLP,把SNLP 构建为一个包装的线性规划(linear programming,LP)。在找到满足传感器网络约束的不同传感器覆盖后,通过为每个传感器覆盖分配时间来使传感器网络寿命最大化。从形式上,对于来自一组={,,…,c}的每个传感器覆盖c来说,就是需要找到时间变量t。构建矩阵C,其行=1,2,…,代表每个传感器(为简化起见,这里用来代替任意传感器p),其列=1,2,…,代表每个覆盖,于是有:
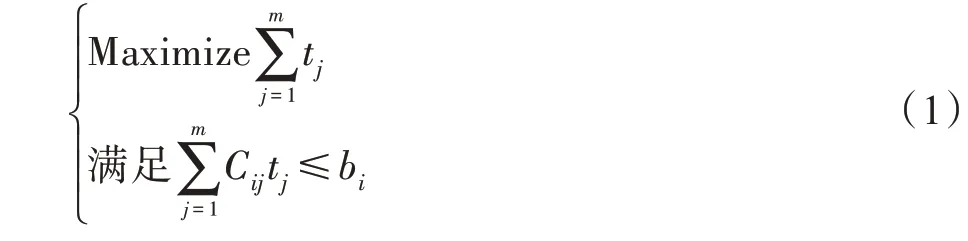
式中,b为传感器的初始能量供给,如果传感器不在覆盖集中,则C=0,否则C=1。
2.1 SNLP 的Garg-Konemann 算法求解
上面的线性规划其实是一个包装的LP。一般来说,一个包装的LP 定义为:

式中,、和有正的元素,把的维数表示为×大小。在本文情况下,的列数不能太大(一般与传感器数量成指数关系),而且采用(1+)近似的Garg-Konemann(龙格-库塔)算法,算法假设LP 通过一个向量∈R和一个寻找使其长度最小化的的列的算法隐含给出。在式(2)中,列关于LP 的长度对于任意正的向量定义为:
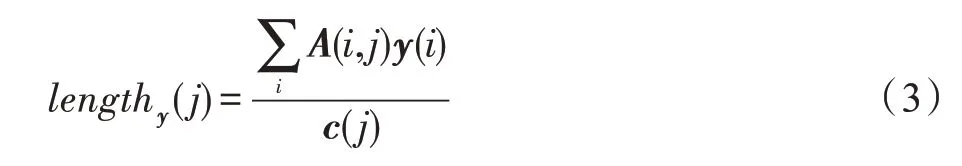
采用(1+)近似Garg-Konemann 算法求解最小长度列的实现伪代码如算法1 所示。
(1+)近似Garg-Konemann 算法
输入:向量∈R,>0 和寻找包装的LP max{|≤,≥0}的最小列长度A问题的(1+)近似Garg-Konemann算法。
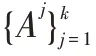
1.初始化:=(1+)((1+)),对于=1,2,…,,()←/(),←,=0
2.While<1
采用-近似GK 算法寻找列A,计算和具有最小()/A()的行的指标

当采用Garg-Konemann算法求解本文式(2)的LP时,即求解最小权值传感器覆盖问题,其中的权值与向量的元素成比例,即对于每个节点=1,2,…,来说,其权值()=1/y。这意味着:对于任意的>0,网络寿命问题可以采用算法1 的(1+) 近似的Garg-Konemann 算法在因子(1+)内近似。
2.2 部分传感器覆盖问题的求解
本节研究最小加权传感器集部分覆盖监测区域的问题。
部分-覆盖问题:给定一个常数∈[0,1],具有面积大小为的监测区域和一组传感器,寻找传感器子集,,…,p,以使:
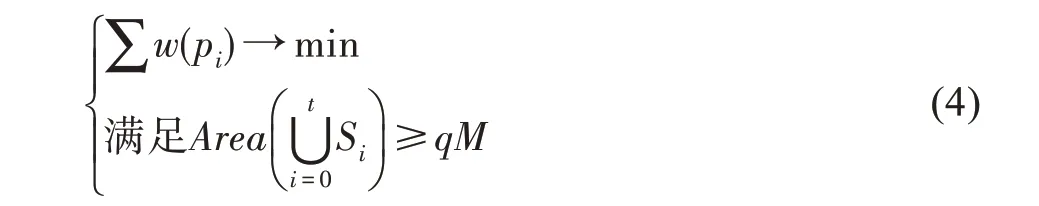
式中,是总的监测区域,S是传感器p的监测区域。
问题(4)可以重新表述如下:
集合-覆盖问题:给定一个有限元素集合,每个元素有成本(每个元素的对应一个面的面积):→R且的系列子集S⊆,每个子集有权值:S→R且∈[0,1],寻找的最小权值子系列覆盖子集⊆,使得被中的集合覆盖的元素的总成本至少为⋅(),这里:


2.3 考虑通信成本的SNLP 求解
假设传感器节点的通信范围至少是其感知范围的2 倍,节点可以处于4 种状态:感知、转发、连接到中心站和空闲状态。每种状态每个时间单位有不同的能量消耗,分别为、、和0。在实际中,≤≤,因为感知节点必须转发它们自己的数据,并使用最多的能量连接到中心站。
一个三元组=(,,)表示由连接到中心站的节点集、中继节点集和感知节点集构成。如果子集是一个覆盖集(也可以是部分覆盖集),则三元组就是可行的,而且中的每个节点要么是中的节点,要么在通信图中通过⋃中的节点连接到中的节点。这时,SNLP 就成为下列具有多变量的包装的线性规划:

式中,t代表三元组使用的时间,=((),(),()),b是节点的初始能量供给。
式(6)实际上是一个加权连接覆盖问题,可以重新表述如下:
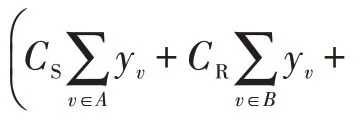
也可以采用Garg-Konemann 算法得到这个加权连接覆盖问题的一个近似解,这里采用一个常数近似算法来求解(对该算法稍微进行改变也可以用于当要求为完全覆盖时的情形),算法求解具体过程如下:
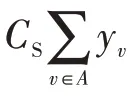
3 SNLP 的分布式调度算法求解
传感器网络寿命还可以通过采用智能自组织的监测调度策略(即分布式调度算法)从本质上得到提高。对此,本文提出一种分布式算法来求解SNLP,算法具有以下优势:(1)更高级的监测区域表示;(2)每个传感器能量供给的动态考虑;(3)可以使活跃传感器集最小化。
为此,进一步假设每个传感器可以与共享面的全部传感器通信。基于1.2 节的数据结构,构建分布式求解算法(自组织监测调度)原理如下:
(1)每个传感器广播自己的id 和地理位置给它的邻居;
(2)每个传感器确定出在它的监测区域内的全部的面,并与覆盖该面的全部传感器的id 的每个面相关联。
采用这种分布式的自组织监测调度,需要解决两个主要问题:(1)每个节点决定是打开还是关闭自己的规则是什么?(2)节点何时作出这样的决定?
首先来描述每个节点的状态和转换规则。
在本文所提出的分布式自组织监测调度算法中,每个传感器在任何时刻为以下3 种状态之一:(1)活跃的,即传感器监测其监控的区域;(2)空闲的,即传感器监听其他传感器,但不监测它的区域;(3)中间脆弱状态,即传感器监测其区域,但应当尽快变换它的状态到活跃的或空闲的状态。每个传感器都知道它的全部邻居处在哪个状态,即任何状态转换都必须立即广播给邻居,连同目前的能量供给。
每个节点的状态转换通过下面的规则来描述:
(1)当一个传感器处于中间脆弱状态时,则它应将其状态改变为:
①如果存在一个不被任何其他活跃的或中间脆弱状态的传感器覆盖的面,则将其状态改变为活跃状态;
②如果它的全部面被具有更大能量供给的活跃或中间脆弱状态的两类传感器中的一种所覆盖,则将其状态改变为空闲状态。
(2)当一个传感器处于活跃或空闲状态时,如果任意相邻传感器变成中间脆弱状态,那么它就应该进入到中间脆弱状态。
一旦任何传感器变成中间脆弱状态,则中间脆弱状态在整个网络上传播,最终每个传感器都处于空闲的或活跃的状态。
把上述过程称为全局重组。每个全局重组需要2(为节点数)次广播,而且得到的全部活跃传感器集构成一个最小的传感器覆盖。
现在来描述全部节点的状态和转换规则,并决定应当何时发生全局重组。显然,几乎完全耗尽能量供给应该是触发事件之一,更准确的调度也需要更频繁的重组,但这又意味着通信成本的增加。本文提出当一个传感器的初始能量供给下降到预先确定的某个阈值时,就启动一个重组,重组触发阈值越小,则执行重组越频繁,将导致更平衡的调度;如果传感器节点间的通信比感知需要更多的能量,则选择局部重组,即把中间脆弱状态的传播限制到触发重组的传感器的某个邻域。算法2 为分布式调度算法实现的伪代码。
分布式调度算法


为了将本文的分布式调度算法与文献[6]的自组织监测调度算法进行比较,还需要在相同情形下进行,即实现无需任何重组的分布式自组织监测调度算法。为此,在实现算法时,一旦传感器节点变成活跃状态,就让它一直活跃,直到耗尽它的全部能量供给。当一个传感器节点几乎完全耗尽其全部能量供给时,就让它向邻居广播。这时,使得空闲传感器的一个最小子集变得活跃起来,以覆盖即将被耗尽能量的传感器所抛弃的面。把这个稍作改进的分布式自组织监测调度算法称为一直活跃分布式调度算法。
4 SNLP 及其求解算法的仿真研究
对本文提出的求解SNLP 的全部算法采用C++实现,并使用GPP-O2 优化编译,在Sun 工作站Ultra-60 上运行,仿真实验在随机生成的测试用例上进行。
仿真实验中取传感器面积为1 000 m×1 000 m,监测面积为800 m×800 m;实验中的传感器节点数分别采用100、200、300、400、500 和1 000 个,每个传感器节点的感知范围为100~150 m,传感器节点的位置随机分布在传感器区域内;覆盖面积分别取100%(=1)和90%(=0.9);对每个传感器节点采用统一分配初始能量供给10(归一化单位时间,下同)和在10~20 之间随机分配;取=0.1,以确保近似Garg-Konemann解的质量;作为比较,仿真实验中给出了近似Garg-Konemann 算法、整数线性规划求解程序CPLEX 算法、分布式调度算法、一直活跃分布式调度算法和文献[6]的自组织监测调度算法的网络寿命比较。
在得到近似Garg-Konemann 算法的传感器覆盖后,就可以通过CPLEX 为每个传感器覆盖分配最佳时间来找到最优调度,约束条件是满足传感器节点的电池需求和使总寿命最大化。
还给出了采用不同重组触发阈值时的分布式算法的通信开销和网络寿命之间的关系。
表1 所示为对于不同感知范围和不同传感器节点数时的面数和近似Garg-Konemann 算法、CPLEX解以及分布式调度算法寻找相同面数时的运行时间。从表1 可见,面的数目随节点数量和/或感知范围的增大而增大,而且找到同样的面数分布式调度算法的运行时间要小于两种集中式算法即近似Garg-Konemann 算法和CPLEX 的运行时间。

表1 不同算法找到相同面数的运行时间Table 1 Running time of finding same number of faces for different algorithms
图3 所示为CPLEX 算法、近似Garg-Konemann 算法、分布式调度算法、一直活跃分布式调度算法和文献[6]的自组织监测调度算法分别在感知范围为100 m,初始能量供给为10 和=1.0 时,感知范围为150 m,初始能量供给在10~20和=1.0时和感知范围为100 m,初始能量供给为10 和=0.9 时对于不同传感器节点数时的网络寿命。从图3 可见,CPLEX 解算法是最优的,因为CPLEX 解是在得到近似Garg-Konemann算法的传感器覆盖后,为每个传感器覆盖分配最佳时间来找到最优调度。当必须覆盖整个监测区域(=1.0)时,从图3(a)和(b)可见,分布式调度算法非常接近集中式的近似Garg-Konemann 算法,但当约束条件为仅覆盖监测区域的90%(=0.9)时,从图3(c)可见,两种分布式调度算法明显比集中算法要差,但本文提出的分布式调度算法总是优于文献[6]的自组织监测调度算法。
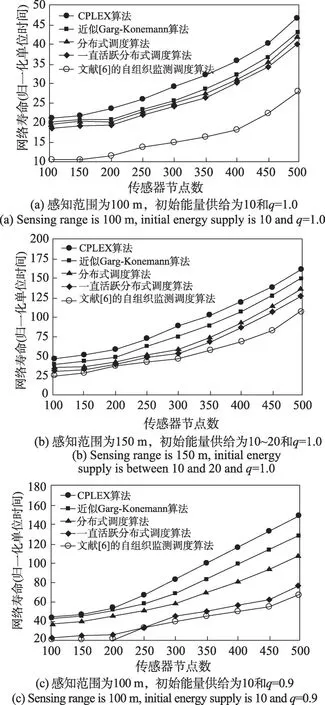
图3 不同算法的网络寿命比较Fig.3 Comparison of network life of different algorithms
表2 所示为对于不同重组触发阈值,分布式调度算法在网络寿命时间和通信开销之间的关系。实验中的感知范围为100 m,初始能量供给在10~20 随机分配。从表2 可见,增大重组触发阈值会降低通信开销,但同时也降低了网络寿命。
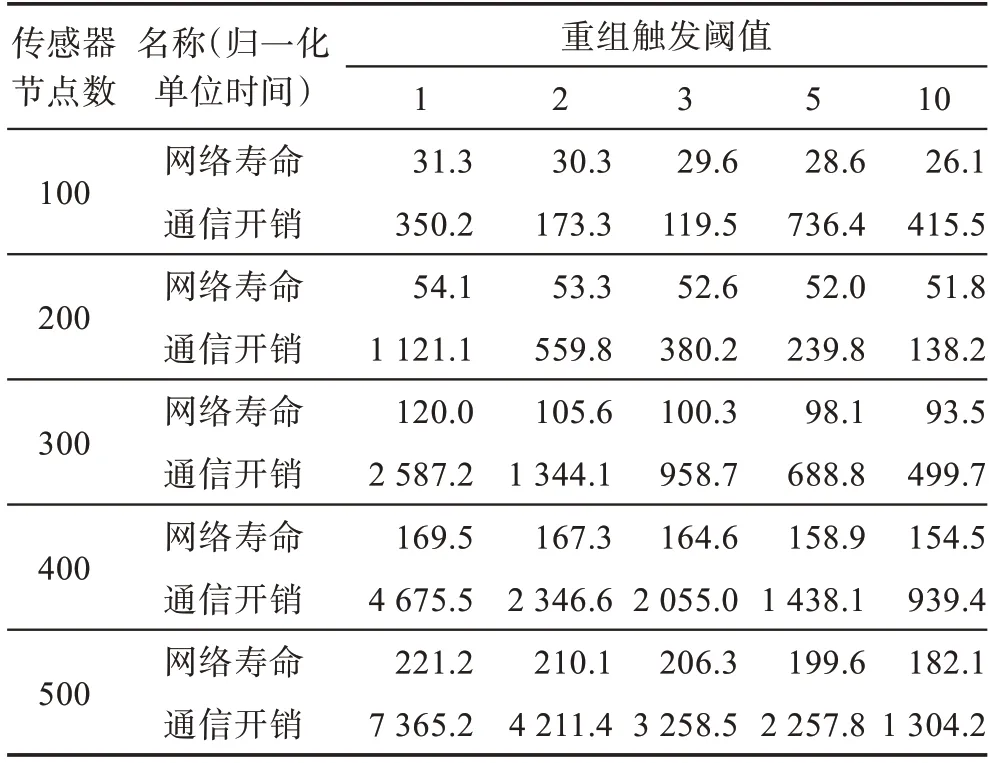
表2 分布式算法的网络寿命和通信开销之间的关系Table 2 Relationship between network life and communication overhead for distributed algorithms
5 结束语
本文构建了一种最大传感器网络寿命问题的传感器网络覆盖模型及其数据结构,并提出了几种集中式和分布式算法来求解这个问题;还研究了监测区域需要部分覆盖时和考虑通信成本时的情形;最后通过仿真实验检验了本文提出的基于传感器网络覆盖模型和数据结构的SNLP 及其求解算法,能够获得较好的运行时间、网络寿命和网络开销。

