基于卷积神经网络的知识图谱补全方法研究

王维美 陈 恒,2 史一民 李冠宇*

1(大连海事大学信息科学技术学院 辽宁 大连 116026)2(大连外国语大学软件学院 辽宁 大连 116044)

0 引 言

知识图谱(Knowledge graph,KG)是种新型知识表示方法，其概念最早由谷歌公司提出，Google认为“things，not strings”，即对于搜索引擎来讲，世界中的各种物体不应该仅仅是string，而是具有实际含义的thing[1]。KG提供图结构化信息，成为智能问答、Web搜索、推荐系统和专家系统等智能应用程序的关键资源。随着知识图谱的兴起，出现了很多大型知识图谱，如Freebase、DBpedia，但这些知识图谱并不完备，知识图谱中实体间隐含的关系没有被充分挖掘，补全三元组成为亟需解决的问题。近几年，很多工作利用卷积神经网络表示知识图谱中实体和关系，并进行知识图谱补全，从而完善知识图谱。

知识图谱是一种描述真实世界客观存在的实体、概念及它们之间关联关系的语义网络[2]，是结构化的语义知识库[3]，其中实体使用节点代替，关系用边表示，表示形式为三元组(h,r,t)，即(头实体，关系，尾实体)。随着知识图谱规模越来越大，三元组数据稀疏问题愈加严重。知识图谱的表示学习技术将三元组中实体和关系表示成向量，在低维向量空间计算实体和关系的语义联系，解决独热学习维度过高和无法有效表示两个实体的问题。知识图谱表示学习面向知识图谱的实体和关系进行学习，该技术可以有效缓解数据稀疏问题，使知识图谱更加完备。

目前一些知识表示学习算法不能有效解决知识图谱存在的数据稀疏问题，如早期的TransE嵌入模型在处理复杂关系上性能降低。对此，本文提出一种基于CNN(卷积神经网络)的知识图谱补全方法。卷积神经网络为计算机视觉而设计，在自然语言处理领域受到很大关注[4]，在某些任务(如分块、词性标签、命名实体识别和关系分类)上取得了不错效果[5]。与全连接神经网络相比，卷积神经网络学习非线性特征可以捕获复杂关系，且参数数量明显减少[6]。基于CNN的优点，使用其进行知识图谱补全的优点在于：(1) 充分考虑到上下文信息和词序，能够学习实体和关系的嵌入向量间的深层联系[6]；(2) 所需参数较少，计算复杂度低，能够适用大规模知识图谱补全。本文方法使用改进的卷积神经网络对三元组(h,r,t)的嵌入矩阵(h,r,t)进行操作，将三元组矩阵和不同的卷积核进行卷积，把卷积得到的特征图进行连接，将特征图和权重向量作点积运算，用点乘的分数判断三元组正确与否。分数越趋近于0，代表三元组越正确，其中正确三元组分数低于错误三元组分数。

本文使用从Freebase和WordNet抽取的数据集，进行知识图谱补全相关的链接预测和三元组分类实验。实验结果表明，本文方法拥有更好的预测精度，补全效果更好。

1 相关工作

1.1 嵌入模型

典型的嵌入模型有TransE[7]、TransH[8]、TransR[9]、TransD[10]等嵌入模型。这些嵌入模型将实体和关系投影到连续的低维向量空间中，即图1中将三元组(h,r,t)投影到低维嵌入空间Rk中，生成(h,r,t)的过程。TransE模型将知识图谱的关系看作是头实体到尾实体的一种平移。给定一个三元组(Beijing,cityOf,China)，TransE将关系向量r作为头实体向量h和尾实体向量t之间的一种平移[11]，即h+r≈t，这也表明在嵌入空间中t应该是h+r最近的邻居[12]。

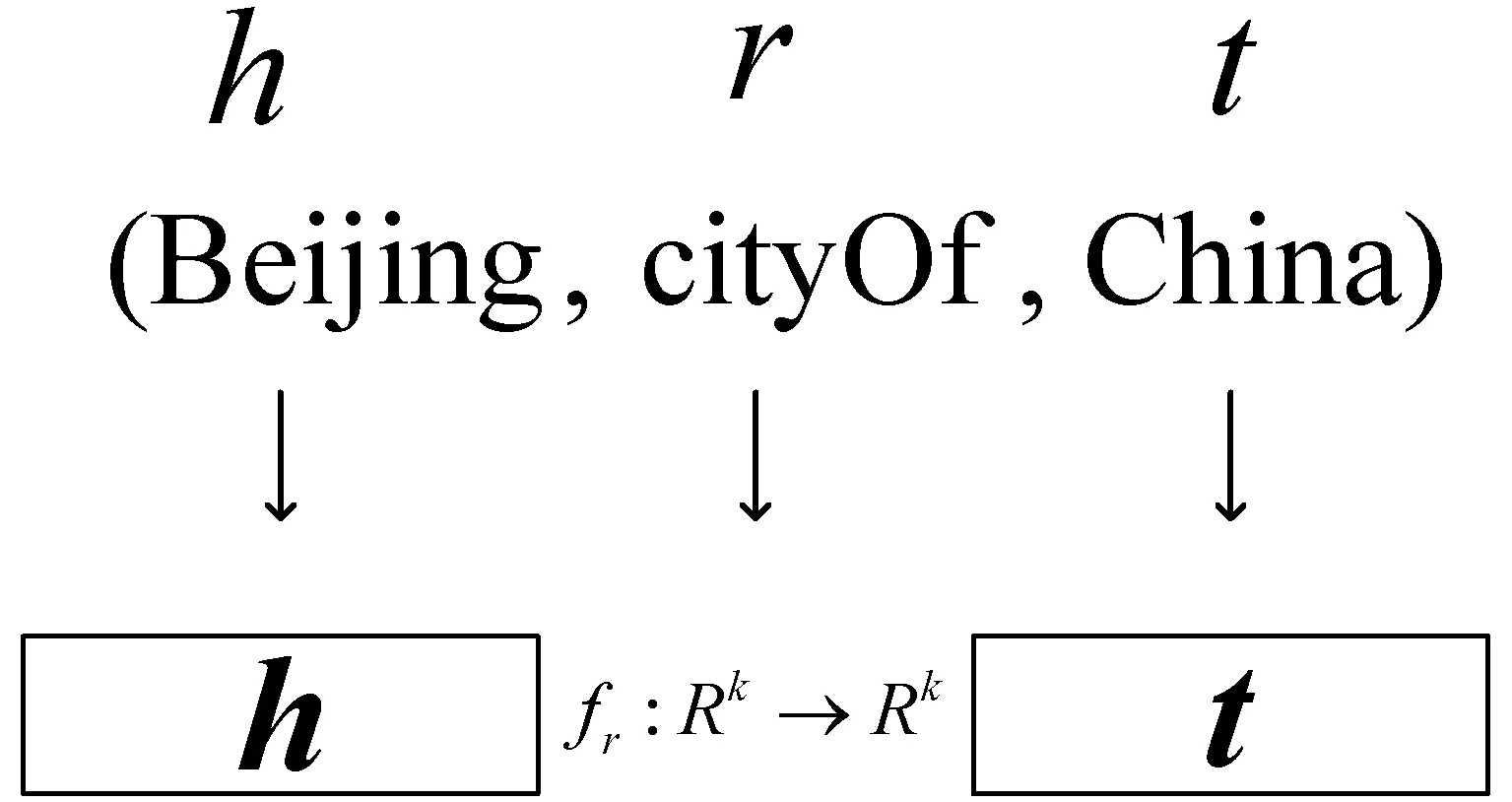
图1 实体和关系的低维嵌入

TransE模型只适用一对一关系，在处理复杂关系类型1-N、N-1、N-N上模型性能显著降低。例如，给定两个三元组(The Terminator，_directed_by，James Cameron)、(Aliens，_ditrected_by，James Cameron),为得到头实体The Terminator和Aliens的向量，使用打分函数h+r≈t进行计算，得到两个相同向量。实体不同，向量就不同，TransE不能有效解决此问题。为了弥补这个缺陷，出现了TransH、TransR等模型。TransR模型对一个给定关系r，定义关系的投影矩阵Mr，将实体从实体空间投影到关系r的子空间，利用打分函数h+r≈t计算每个三元组的得分。TransR通过将实体和关系投影到不同的空间，解决了实体和关系属于不同对象时，不能用同一个空间表示的问题。基于TransR这种特性，本文用TransR对数据集中所有三元组进行训练，将得到的向量作为本文算法的输入，使得每个三元组输入时拥有一定的语义信息。

1.2 神经网络模型

上述嵌入模型仅表达了三元组结构信息，没有利用实体或关系的描述文本。文献[13]提出了一种张量神经网络(NTN)，用实体名称所有词向量平均值表示该实体，让具有类似名称的实体能够共享文本信息。DKRL[14]使用连续词袋(CBOW)以及卷积神经网络(CNN)两种表示学习方法来建立实体描述文本的语义向量。OOKB[15]模型是一种基于图神经网络(Graph-NNs)的模型，将图谱中头实体和尾实体向量进行组合，形成最终向量。此外，模型DisMult[16]和ComplEx[17]使用向量点乘计算三元组得分，利用打分函数判定其正确性。

和链接预测模型DisMult相比，ConvE[18]模型参数少，计算复杂度低，可以高效训练三元组，获取实体和关系的向量嵌入，同时学习三元组更多的特征表示。ConvE作为使用CNN来补全知识图谱的模型，将头实体和关系向量重组，组合成矩阵作为CNN卷积层的输入，使用不同的卷积核进行卷积，输出多个特征图，将这些特征图矢量化，映射成一个向量，此向量和尾实体作点积运算得到三元组分数，利用得分判断三元组的正确性。ConvE模型打分函数见表1。ConvE将头实体和关系作为输入矩阵，忽略了三元组的全局特征。为了使用三元组的全局特征，文献[6]提出了ConvKB模型，该模型将三元组(头实体，关系，尾实体)矩阵作为输入，捕获三元组全局特征，利用不同的卷积核进行卷积，通过打分函数得到每个三元组的得分，作为判断三元组正确的依据。从上述两个模型可以看出，卷积神经网络可以提取三元组中实体和关系的特征，然后和不同的卷积核进行卷积，得到相应的特征图，将特征图进行连接得到三元组的整体特征。文献[6]提出使用CNN对三元组进行编码，但只融合进了TransE，没做进一步探索。为充分考虑三元组的结构信息和特征表示，本文使用TransR训练出的三元组矩阵作为本文算法的输入，解决TransE模型不能建模复杂关系的缺陷，同时使用不同的卷积核进行卷积。本文对卷积核形状做了一定修改，同时设置不同的步长数对输入矩阵作卷积运算，对输入的三元组尽可能捕获更多的特征，获取三元组的全局表示特征。以上模型的打分函数如表1所示。

表1 相关模型的打分函数

2 算法设计

使用TransR模型训练出的三元组矩阵作为本文算法的输入，并在TransR模型算法的基础上完善了基于卷积神经网络的算法。给定一个三元组(h,r,t)∈T,h,r∈E,r∈R，即KG=(E,R,T)，E为实体集，R是关系集，T是训练集，每个实体和关系的嵌入维度为N。本文算法如下：

输入：训练集T=(h,r,t),实体集E，关系集R，正则项权重λ，嵌入层维度N。

初始化:

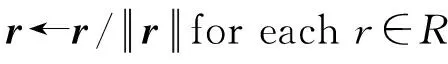
Loop:

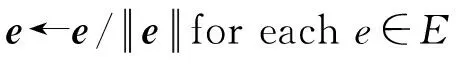
Tbatch←sample(T,b)

//sample a minibatch ofb

Tbatch←∅

for(h,r,t)∈Tbatchdo

Tbatch←Tbatch∪{((h,r,t), (h′,r′,t′))}

endfor

更新嵌入层

Input←[h,r,t]

//输入矩阵

计算concat(g([h,r,t]*Ω))·w

更新损失函数

//θ=±1

EndLoop

本文算法框架图如图2所示。使用(h,r,t)表示每个三元组(h,r,t)相应的嵌入矩阵，令M=[h,r,t]∈RN×3,Mi,:∈R2×3表示矩阵的每一行，和不同的卷积核进行卷积。ω是一个2×3的卷积核，和M的每两行重复卷积，得到一个个特征图，连接所有特征图得到的列向量如式(1)所示。

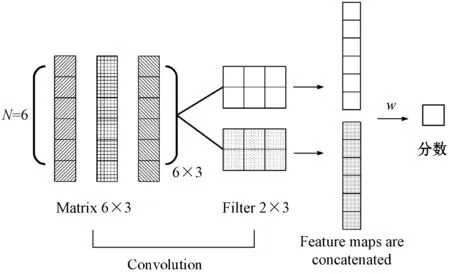
图2 算法框架

v=[g(ω·M1,:+b),g(ω·M2,:+b),…,

g(ω·Mk,:+b)]∈RN

(1)

列向量和权重向量作点积运算，得到的分数作为判断三元组是否正确的依据。本文采用不同卷积核进行操作，形状为2×3，步长为{1,2,3}，令步长为1，卷积核数量|ω|=m,会产生m个不同的特征图，m个不同特征图进行连接得到一个列向量v∈Rm(N-1)，然后和一个权重向量w∈Rm(N-1)作点乘。其中，打分函数越小代表三元组越正确，打分函数如下：

f(h,t)=concat(g([h,r,t]*Ω))·w

(2)

式中：Ω和w分别是卷积核集、权重，它们都是超参数；g代表激活函数，本文比较了ReLU和Sigmoid两个激活函数，实验结果表明，ReLU卷积效果更好；*代表卷积操作；concat表示连接操作；[h,r,t]表示算法的输入矩阵，此矩阵由本文改进后的TransR模型进行训练得到。最小化损失函数作为最终的训练目标，损失函数如下：

(3)

T′={(h,r,t)|h′∈E}∪{(h,r,t)|t′∈E}

(4)

即将正确三元组的头实体和尾实体分别用数据集所有实体代替，正例三元组得分低于负例三元组得分。本文使用Adam[20]最小化如式(3)所示的损失函数。

3 实 验

3.1 数据集

本文使用从Freebase和WordNet中抽取的3个数据集：FB15k[7]、WN18RR[18]、FB15K-237[20]进行实验。由文献[20]可知，数据集WN18和FB15k包含一些反转关系，这些反转关系会使实验结果显著提高，为保证实验结果的准确性，将数据集WN18和FB15k中具有反转关系的三元组去掉，得到对应数据集WN18RR和FB15K-237。

数据集FB15k包含1 345种关系，14 951个实体，592 213个三元组，训练集、验证集、测试集大致比率为9 ∶1 ∶1。

数据集FB15K-237包含237种关系，14 541个实体，310 116个三元组，训练集、验证集、测试集大致比率为14 ∶1 ∶1。

数据集WN18RR包含11种关系，40 943个实体，93 003个三元组，分为训练集、验证集、测试集3种，大致比率为28 ∶1 ∶1。

数据集统计情况如表2所示。

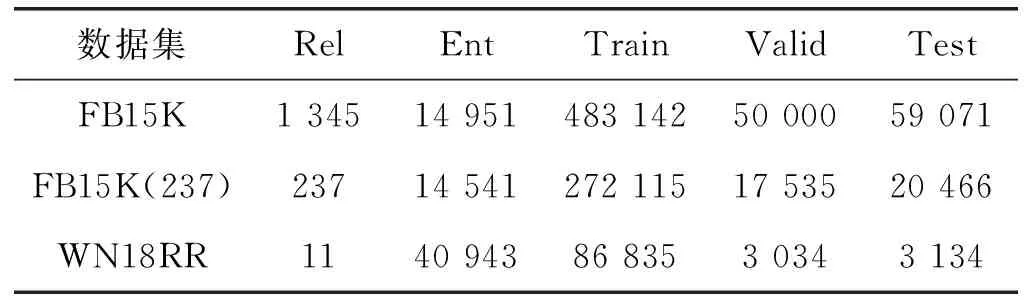
表2 数据集统计

3.2 参数设置

本文使用改进后的TransR训练出三元组矩阵来作为本文算法的输入。使用超参数网格搜索训练TransR 3 000次，最终超参数设置如下：数据集的嵌入维度N∈{50,100}，SGD的学习速率λ1∈{0.1,0.01,0.001,0.000 1},间隔γ∈{1,2,3,4,5},归一化采用L1或L2范数。

为了学习实体和关系的嵌入维度N、卷积核ω、权重w、偏置项b这些超参数，本文使用Adam优化器，其学习速率λ2∈{0.01,0.001,0.000 1,0.000 5,0.000 01,0.000 05}。卷积核ω的数值随机初始化，卷积核数量m∈{100,150,200,300,400,600}，损失函数的λ值设置为0.001，所有实验进行500轮的迭代训练。此外，为有效缓解过拟合，根据验证集上的MRR评估指标，通过网格搜索选择dropout值，其值为dropout∈{0.1,0.2,0.3,0.5}。

在经过500次迭代训练后，使用最后一次迭代训练的输出值作为测试集评估，不同数据集最优Hit@10如下：在WN18RR上，Hit@10最优设置为：N=50，m=600，λ2=0.000 5，dropout=0.5；在FBI5K-237上，Hit@10最优设置为：N=100，m=100，λ2=0.000 01，dropout=0.3。

3.3 链接预测

3.3.1实验设计

链接预测即预测知识图谱中三元组缺失的实体和实体间关系。例如：给定三元组(Michelle Obama,residence,?)，其中：头实体为Michelle Obama，关系为residence，尾实体缺失，为补全三元组，将American添加到该元组中，对其进行补全；或者(邓超，？，孙俪)，该三元组中缺失关系，为补全三元组，将夫妻(或配偶)关系添加进去进行补全。实验采用文献[7]的标准，对测试集中每个三元组(h,r,t)，把头实体、尾实体去掉，依次使用数据集所有实体替代，得到负例三元组，对新三元组使用打分函数计算相似性得分，相似度越高排名越靠前，这样可以得到正确实体的真实排名。

3.3.2评估指标

本文选择平均排名MR(MeanRank)、倒数平均排名MRR(Mean Reciprocal Rank)、进入前10名的比例(Hit@10)作为本文算法评估指标。三个指标中，MR越低、MRR越高、Hit@10越高，代表算法的效果越好，学习能力越强。数据集中可能存在一些错误三元组，采用文献[7]的标准，把错误三元组从数据集中删除，删除后的设置为Filter，原来的为Raw。在数据集FB15K-237和WN18RR上，仅使用Filter设置。

3.3.3实验结果和分析

采用相同实验设置情况下，本文实验环境为：Window 7 64位系统，物理内存为8 GB。数据集WN18RR和FB15K-237在不同模型下的链接预测结果如表3和表4所示。

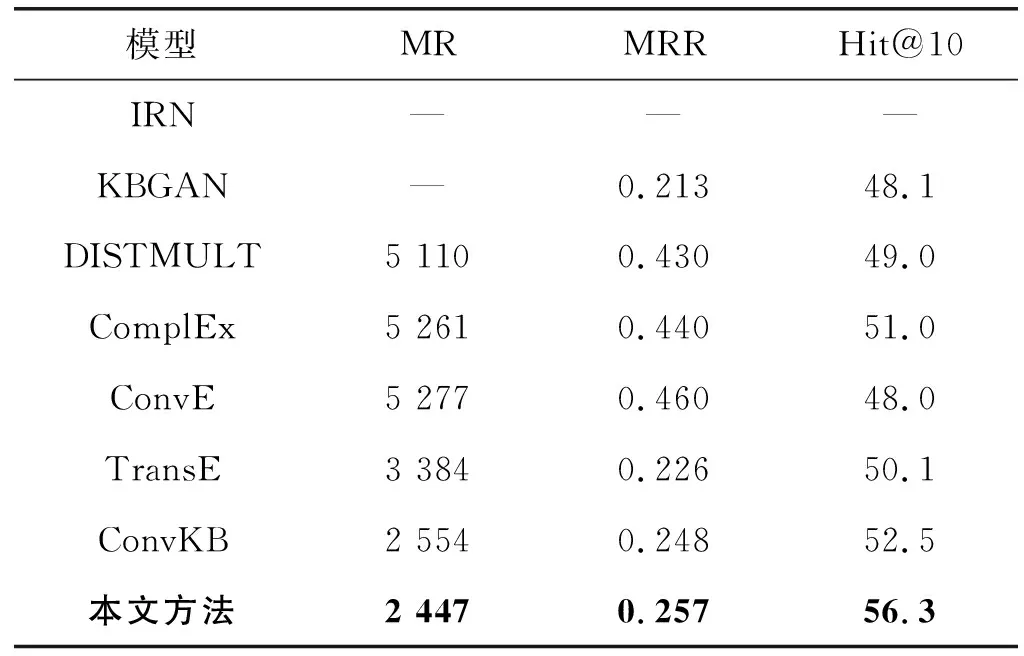
表3 WN18RR在不同模型下链接预测结果

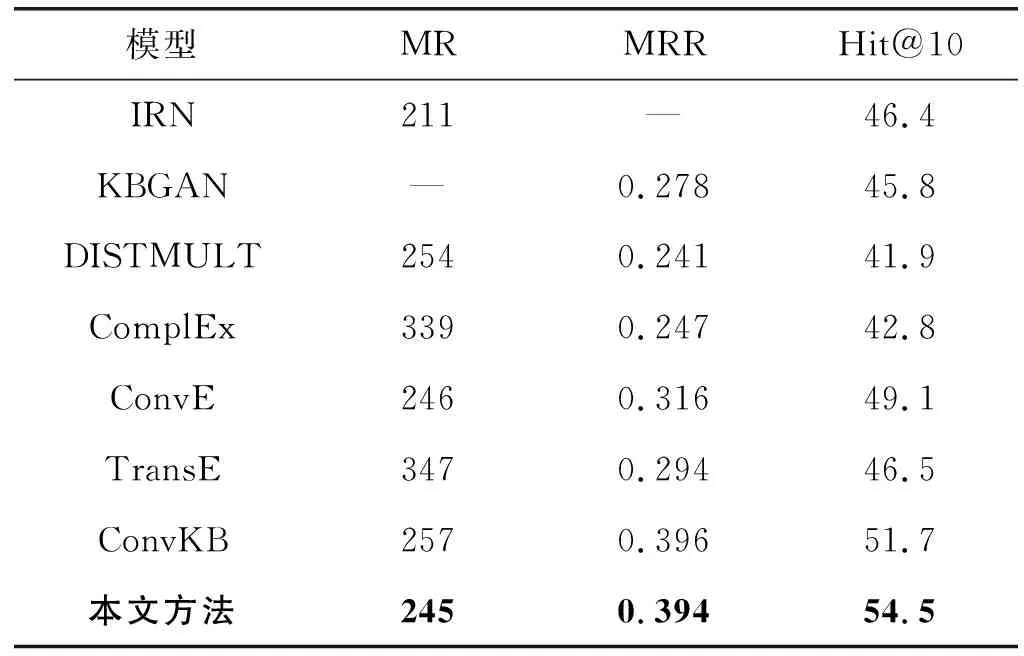
表4 FB15K-237在不同模型下链接预测结果

可以看出，本文方法在WN18RR和FB15K-237数据集上均获得了最低的MR和最高的Hit@10。具体分析如下：(1) 本文方法与ConvKB模型相比，数据集WN18RR在MR上降低了4.2%，在Hit@10上提高了3.8;数据集FB15K-237在MR上降低了4.7%，在Hit@10上提高了2.8。(2) 在数据集WN18RR上，TransE模型的MR指标优于ConvE、ComplEx等模型；TransE模型的Hit@10指标优于ConvE、DISTMUL等模型。可见，基准模型TransE在数据集WN18RR上具有很好的表示效果。(3) 和其他模型相比，本文方法具有更好的表示能力，也说明了改进的卷积神经网络用于知识图谱补全具有更好的性能。

3.4 三元组分类

3.4.1实验设计

三元组分类即判断知识图谱中三元组的正确性。引用文献[9]提出的三元组分类，设置一个阈值，对于任意给定的三元组，使用式(2)所示的打分函数计算得分，如果这个得分低于阈值，则三元组是正确的，否则为错误。

3.4.2实验结果和分析

参照文献[9]，本文使用基准数据集FB15K进行三元组分类实验。实验环境为Window 7 64位系统，物理内存为8 GB。FB15K最优参数为N=100，m=300，λ2=0.000 05,dropout=0.1。实验结果如表5所示。

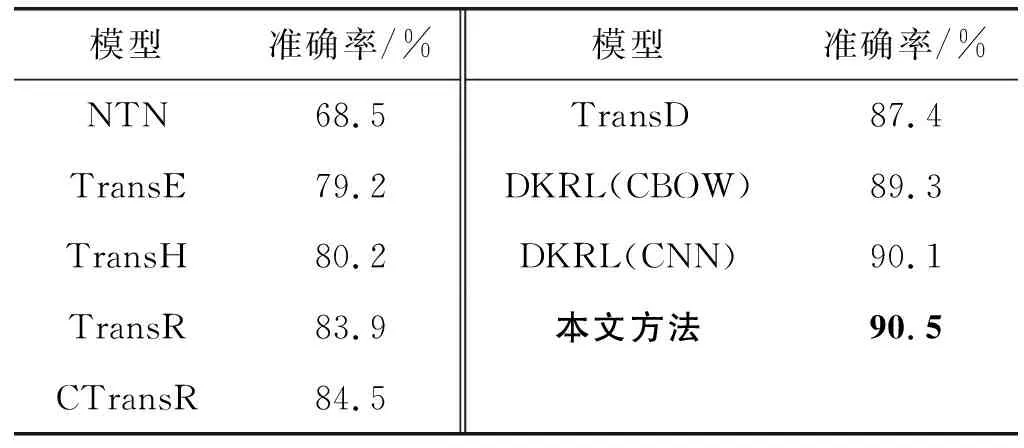
表5 三元组分类实验结果

可以看出：(1) 本文方法取得了90.5%的准确率，优于DKRL模型,证明在三元组分类这个任务上本文方法效果更好。(2) 基于表示学习的嵌入模型效果都要好于NTN，说明将关系看作头实体到尾实体的平移的嵌入模型更能表示知识图谱中的数据和区分正确的三元组。

4 结 语

本文针对知识图谱补全提出一种基于卷积神经网络的方法，利用三元组全局信息，将三元组矩阵作为算法的输入，和不同的卷积核进行卷积操作，得到不同的特征图，将这些特征图进行连接，得到的向量和权重作点积运算产生一个得分，分数越低三元组越正确。

(1) 三元组分类实验结果表明，本文方法优于一些传统嵌入模型，在链接预测实验中，在MR、MRR、Hit@10指标上有了明显提高，从这三个指标可以看出本文方法解决了知识图谱中数据稀疏问题，提高了知识图谱的完备性。

(2) 本文方法可以对普通知识图谱和领域性知识图谱进行补全，同时也可以应用到查询系统，比如建模三元组(查询，用户，文档)，通过查找三元组中缺失的实体或关系，将缺失的实体或关系以三元组的形式添加到数据库中，从而对数据库进行补全扩充。

另外，针对得到的实体或关系与已有实体关系存在不相容或冲突问题：使用本文方法判断不同三元组得分，利用分数判断三元组正确性；使用实体或关系对齐模型来判断不同三元组的正确性，若三元组正确，则在知识图谱中可以共存，比如：姚明亦指大姚(别名)。

为提高三元组补全正确率，今后的研究将尝试修改卷积神经网络内部架构，对三元组特征提取作更深入的研究；将实体和关系的描述文本融入到卷积神经网络中，作为算法的输入。