HMCTC:一种新型的高效时序隐信道

肖

汉1,2,杨 威1,3,沈 瑶1,3,张宇飞1,2,黄刘生1,3

1 引 言

随着信息化的高速发展,网络通信已经成为了人们生活中不可或缺的一部分.然而,信息化在带给人们高效和便利生活的同时,信息安全问题也随之而来.安全事件层出不穷,陆续出现了苹果“泄密门”事件、12306用户资料大规模泄漏事件等重大的安全事件.越来越多的国家把信息控制与能力视为国家安全的标志[1].

传统的保护信息安全的方式往往是对要传输的信息进行加密,但是加密的通信链路往往会引起攻击者的注意.随着计算机硬件和密码学的高速发展,攻击者破解密钥的能力有了较大的提升,加密的通信链路已经无法充分保障数据通信的安全.而网络隐信道是一种新兴的信息隐藏技术,是一种借助于正常通信信道传输隐秘信息的通信方式.其具有较高的隐秘性,能轻而易举通过防火墙、控制访问等网络安全设施,让第三方难以发现踪迹[2].所以利用网络隐信道进行隐秘通信受到人们越来越多的关注.

网络隐信道根据其载体不同主要分为两大类:一是存储型隐信道,存储型隐信道主要是利用网络传输协议的缺陷,在协议的未用或保留字段中嵌入隐秘信息.例如Identification、TOS、URG等协议字段[4,5];二是时序型隐信道,时序型隐信道往往通过操纵数据包之间的时序关系,将隐秘信息隐藏在数据包的时序分布中[6,8-12].例如通过调制数据包的发送时间来传递隐秘信息.存储型隐信道的隐蔽性较低,且很容易被防火墙等安全设施发现并摧毁.而时序型隐信道往往传输速率低,而且其隐蔽性虽然相对于存储型隐信道较高,但也很难逃过专业检测算法的检测[7,9,17].

一个好的时序型隐信道必须具有高容量和强隐蔽性等特点.高容量就是隐信道要具有较高的传输速率;强隐蔽性就是具有较高的抗检测性,能躲过安全设施的检测.而现有的隐信道往往侧重于研究隐信道的隐蔽性或信道容量某一方面,没有将二者有机的统一起来.而我们提出的HMCTC隐信道在采用了K元Huffman编码的基础上调制出符合合法信道时序间隔分布的时序间隔序列,从而使HMCTC隐信道能够在保证隐蔽性的同时具有较高的信道容量.总的来说,本文的主要贡献如下:

1)我们提出一种新型的高效时序隐信道HMCTC,相对于传统隐信道,其具有较高的信道容量和较强的隐蔽性,能够高速且安全的完成隐秘信息的传输.

2)在HMCTC隐信道中,我们将Huffman编码应用到了隐信道的编码阶段.采用K元Huffman编码对隐秘信息的信源符号进行编码,压缩信源符号的码长,从而提高HMCTC隐信道的信道容量.理论上来讲,HMCTC隐信道的信道容量会随着K的增大而不断增长.

3)针对HMCTC隐信道的隐蔽性,我们通过调制其编码,逆向生成和合法信道服从同一分布的时序间隔序列,从而保证HMCTC隐信道具有较强的隐蔽性.

4)我们针对HMCTC隐信道的信道容量和隐蔽性设计并完成了一系列实验,实验表明,相对已有的时序隐信道,HMCTC隐信道具有较高的信道容量和较强的隐蔽性.

本文后续部分包括:第2节是前人在隐信道方面的相关工作,主要介绍隐信道的发展历史和研究近况,第3节主要介绍了HMCTC隐信道编码本的构建,第4节为HMCTC隐信道的具体实现机制,第5节分析了其信道容量与变量K之间的关系,第6节是对HMCTC隐信道的信道容量和隐蔽性进行实验验证,第7节则是对论文的总结.

2 相关工作

1973年Lampson首次提出隐信道的概念[3],并给出了隐蔽信道的一般通信模型.在1987年,Girling第一次提出基于网络协议的隐信道[4](简称网络隐信道),即利用网络传输协议构建隐信道.之后,Padlipsky,Rowland等[5,8]相继提出了在互联网传输协议中构建隐信道的方法.

Cabuk等人在2004年提出了一种基于TCP/IP的二进制时序型隐信道IPCTC[9],通信双方约定固定大小的时序窗口t,接收方通过判断是否在时序窗口t内收到数据包来确定传输的隐秘信息,例如收到数据包代表′1′,没收到代表′0′.IPCTC是一种简单的时序型隐信道,它需要通信双方保持传输同步从而保证解码的正确性.但是这种隐信道容量较小,实验表明当t=60ms且RTT=31.5ms时,IPCTC隐信道的容量只有16.67bps.同时由于其时序分布具有很强的规律性,其统计特征和正常信道差别较大,很容易被检测工具检测出来.

Shah等人发明了一种基于键盘设备的叫做JitterBug的时序型隐信道[10],它主要工作在用户利用键盘进行输入的阶段.在用户敲击键盘的过程中改变数据包的发送时间从而构造时序隐信道来传输隐秘信息.通过他们的编码传输方案,用户每一次按键都能传送1bit信息,隐秘信息的传输速率取决于用户输入的速度.在此基础上,他们又提出了一种新的编码传输方案,一次按键可以传输4bit的隐秘信息.这种方案大大的提高了隐信道的传输速率,但是这种隐信道的传输速率仍旧受到用户键盘输入速度的限制.同时一些较为精细的检测算法[9,17]仍能检测到其异常的时序特征.

Sellke等人提出一种复杂的基于密码本的时序型隐信道[11],简称L-to-N隐信道.这种隐信道采用的是一种叫做“L-bits toN- packets”的机制,即每一串L-bit的二进制流对应N个时序间隔(T1,T2,T3,…,TK).发送方将要发送L-bit的二进制流根据密码本转换成N个时序间隔.而接收方每收到N个时序间隔就根据其密码本将其转换为对应的L-bit的二进制流.Sellke分析并验证了不同的L和N取值时对隐信道容量的影响.当使用“L-bits toN- packets”时,其隐信道容量高达近37bps,具有较高的信道容量.但是这种隐信道的时序分布特征也较为明显,其隐蔽性较差.

Gianvecchio等人设计了一种“Model-based”隐信道[12].通过不断获取合法信道的数据包,分析其时序分布特征,确定合适的拟合模型,然后通过将要传输的隐秘信息调制成选定模型的时序序列进行传输.由于这种隐信道的时序分布与合法信道时序分布较为拟合,其区分度较小,所以具有较强的隐蔽性.但是这种隐信道容量不高.总的来说这是一种低信道容量高隐蔽性的时序型隐信道.

本文提出的HMCTC隐信道首先利用K元Huffman编码将常见的信源字符进行编码,即将要传输的隐秘信息根据编码本进行重新编码重写,从而用较短的向量序列表示较长的隐秘信息,然后根据合法信道的i.i.d.(independent and identically distributed)[16]对要传输的向量序列进行拟合调制,使得调制产生后的时序间隔序列符合合法信道的i.i.d..这样HMCTC隐信道就能够保证在具有较高容量的同时拥有较强的隐蔽性.

3 编码本构建

ASCII码编码是国际上通用且最常见的编码,使用8bit定长的二进制序列表示常见的128个字符(包括可打印的和不可打印的).但是这种编码方法会造成很大的信息冗余,不是最佳编码.而Huffman编码[13]则是根据符号的频率进行变长编码,频率高的字符的码长较短,频率低的字符码长较长.理论表明,Huffman编码是一种最优编码,其构造出来的编码方案使得平均码长达到最小.而K元Huffman编码是对常见Huffman编码的一种扩展,理论上来说,随着K的增加,其平均码长会逐渐减小.图1是一个给定的字符频率表经过K元Huffman编码后的平均码长.从图1中可以看出,随着K的增加,字符的平均码长逐渐较小并接近于1.

利用K元Huffman编码构造编码本的过程如下:

1)将要编码的n个信源符号根据其概率的大小进行排列:

p1≤p2≤p3…≤pn

2)取K个概率最小的信源符号按升序分别分配1、2、3…K这K个码元,并将这K个信源符号的概率相加作为一个p1≤p2≤p3…≤pn新的信源符号的概率,与未分配码元的信源符号进行重新排列.

3)对重排后的信源符号重复进行步骤2)的工作,直到所有的信源符号都成功分配到码元.

4)从最后一级开始,向前返回得到n个信源符号所对应的码元序列,这个码元序列即信源符号的码字.

5)记录n个信源符号与其码字的对应关系,完成编码本的构建.

图1 K元Huffman编码平均码长Fig.1 Average code length of K-array Huffman-encoding

假设要编码信源符号序列为X={A,B,C,D,E,F,G},其对应的概率序列P={0.1,0.2,0.4,0.05,0.06,0.12,0.07},则利用3元Huffman编码构造编码本的过程如图2所示.

图2 3元Huffman编码本构造过程Fig.2 Encoding process of 3-array Huffman-encoding

4 实现机制

HMCTC隐信道的通信架构如图3所示,发送方首先对将隐秘信息根据密码本进行编码,然后对编码后的信息进行模拟调制,生成符合合法信道i.i.d.分布的时序间隔序列,最后按照生成的时序间隔序列发送数据包.而接收方首先获取数据包之间的时序间隔序列,然后逆向解调获取编码过的信息,最后根据编码本恢复隐秘信息.其中编码本是利用K元Huffman编码进行构造的,通信双方共享同一个编码本.

4.1 发送方机制

图3 HMCTC隐信道通信架构Fig.3 Communication framework of HMCTC covert channel

2)调制.利用基于共享密钥Kkey的伪随机数产生器(通信双方共同约定)产生n个服从(0,1)均匀分布的随机数序列{r1,r2,r3,…,rn}使用公式

ui=(mi+ri)mod1

(1)

产生n个服从(0,1)均匀分布的随机序列{u1,u2,u3,…,un}.假设F(X)是合法信道的时序间隔分布的概率分布函数.令

di=F-1(ui)

(2)

生成调制后的时序间隔序列{d1,d2,d3,…,dn}.

3)发送.选取一条正常通信信道上的n+1个数据包P=(p1,p2,…,pn+1),调制这n+1个数据包的发送时间,使其满足|Ts(pi+1)-Ts(pi)|=di(1≤i≤n).其中Ts(pi)代表第i个数据包的发送时间.

4.2 接收方机制

(3)

(4)

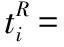
(5)

5 信道容量和K取值

信道容量表示的是一个通信隐信道在保证信息正确率的前提下所能达到的最大信息传输率.往往通过计算单位时间内传输的信息比特数来衡量信道容量[14],即

(6)

其中I(t)代表在时间t内传输的比特数.

因为编码阶段采用的是K元Huffman编码,所以字符编码的平均编码长度L*为

L*=∑(pi*Li)

(7)

其中,Li代表字符的编码长度,pi代表字符i的概率.由于调制后的隐信道时序间隔序列是与合法信道的时序间隔序列服从同一分布,其对应的概率密度函数为f(x)=F′(x),数学期望为E(X),则其单位时间内发送的数据包数S为

(8)

所以根据公式(7)、(8)可知,HMCTC隐信道的信道容量

(9)

(10)

其中HK(X)是对信源符号向量X进行K元Huffman编码后的熵.从公式(9)、(10)可以看出,K的取值会影响信道容量.当K增大时,其平均编码长度L*随之减小,信道容量C随之增大.但是K的值并不可以无限增大,这是因为网络通信并不稳定,网络抖动或拥塞会导致时序的变化,影响解码的正确性.假设时序波动为θi,则在解调的过程中

(11)

其中δ∈(di-θi,di+θi).联立公式(2)、(4)、(11)可得

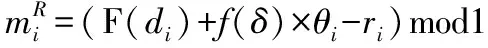
(12)

所以为了保证解码的正确性,根据公式(5)可知,必须要保证

(13)

即

K<(2×|max(f(x))×θmax|)-1

(14)

由以上证明可以看出,当K增大时,隐信道的信道容量随之增大.但K不可以无限制增大,当

K≥(2×|max(f(x))×θmax|)-1

(15)

时,将无法保证解码的正确性.

6 实验与结果

我们的测试环境是选取两台服务器分别作为隐信道的发送端和接收端进行通信.发送端按照隐信道的调制方法在客户端的通信协议栈中控制数据包之间的时序间隔,而接收端通过解析通信中数据包之间的时序间隔从而解码还原客户端发送的隐秘信息.

为了测试我们隐信道的功效,我们利用Telnet通信流构造HMCTC隐信道.为了选取合适的调制函数,我们在中科大苏州研究院的网关服务器上抓取Telnet通信包,对各条通信流进行时序间隔序列统计分析,发现其时序间隔分布与Weibull分布(如图4所示)较为相似,其中Weibull分布概率密度函数为

(16)

根据样本使用最大似然估计法[16],我们可以得到其具体分布的参数值,其中a=200.3129,b=0.9012.

图4 样本分布和weibull分布对比Fig.4 Compare between sample distribution and weibull distribution

6.1 容量分析

由于网络环境是固定的,其最大时序波动也就可以认为是一个定值,在最大时序波动θmax固定的情况下,HMCTC隐信道在不同的K取值情况下,分别传输20篇英文文章,用其平均传输速率估计每一个K值对应的信道容量.以此我们来分析K的取值对隐信道容量的影响.

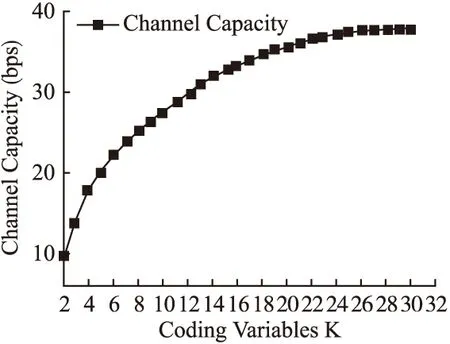
图5 信道容量与编码变量K的关系Fig.5 Relationship between channel capacity and coding variables K

从图5可知,HMCTC隐信道的信道容量随着K的增长而不断增大.但是K值并不可以无限增大,根据公式(14)可以计算出,在此次实验环境中,K的最大值为26,即当K=26时,其信道容量容量能达到最大.当其超过其最大值时,其误码率会超过30%.所以在此次实验中,在保证解码准确的情况下,HMCTC隐信道的最大容量为37.79bits/s.相对于L-to-N隐信道(Δ=50ms,δ=10ms)的36.59bits/s[11]和IPCTC(Δ=50ms,δ=0ms)19.86bits/s[9]其隐信道的容量分别提升了0.03%和90.28%.

总的来说,HMCTC的隐信道的容量主要取决于所选取的正常信道的传输速率和K的取值.由于所选取的正常信道的速率是固定的,所以其信道容量主要由K的取值来确定.实验表明,HMCTC隐信道的信道容量随着K的增长而不断增大,当K取其最大值时,其信道容量达到最大.所以说HMCTC具有较高的信道容量,其信道容量是能够得到保证的.

6.2 隐蔽性分析

为了验证HMCTC隐信道的隐蔽性,我们采用ε-相似度检测算法[9]和熵检测算法[17]分别对HMCTC隐信道、合法信道、L-to-N隐信道、IPCTC隐信道进行检测,从实验方面验证HMCTC隐信道的隐蔽性.

图6 ε-相似度检测百分比图Fig.6 Percentages for samples using ε-Similarity Detection

熵检测.信息熵率是指随机变量的平均信息熵,常用于衡量随机变量的复杂度和规律性[13].由于隐信道的规律性较强,混乱程度小,相对于正常信道拥有较小的信息熵值,所以熵检测算法可以通过计算时序间隔{d1,d2,d3…dn}的信息熵entropy=-∑pilogpi来判断信道是否为隐信道.其中pi是对应项di出现的概率.图7是HMCTC隐信道、正常信道、L-to-N隐信道、IPCTC隐信道在样本大小为500的情况下,各个样本的信息熵值分布.从图中可以看出,合法信道与L-to-N隐信道、IPCTC隐信道的熵值相差较大,利用熵检测算法能够轻易检测出L-to-N隐信道、IPCTC隐信道是否存在.但是HMCTC隐信道的熵值与合法信道的熵值的区分度较小,所以说很难通过熵检测算法检测出HMCTC隐信道的存在.

选取大量数据进行实验,确定ε-相似度检测算法和熵检测检测算法最优的参数,然后对四种信道的产生的数据以窗口大小为500进行分组检测.其最终检测判定结果如下表表1所示,其结果为检测准确率.

图7 熵检测信息熵值分布图Fig.7 Information entropy for samples using entropy detection

从以上的结果中可以看出,常用的检测算法对一些常用的隐信道有着较好的检测效果,但却很难检测到HMCTC隐信道,说明HMCTC隐信道有着较好的隐蔽性,很难被常用的隐信道检测算法识别.

表1 信道检测结果
Table 1 Results of detection

Channelε⁃SimilarityDetectionEntropyDetectionLegitimateTelnetChannel100%100%HMCTCCovertChannel0．2%0．4%L⁃to⁃NCovertChannel100%100%IPCTCCovertChannel100%100%

7 总 结

本文中提出了一种新的基于K元Huffman编码的时序型隐信道,也称HMCTC隐信道.传统的隐信道往往不能保证高信道容量和强隐蔽性的统一.而HMCTC隐信道克服了这个缺点,在保证较强隐秘性的同时又拥有较高的信道容量.在本文中我们详细介绍了HMCTC隐信道的实现原理,并验证了它的高信道容量和高隐蔽性.将来我们会研究进一步增强该隐信道容量的方法及相应的检测方法.

[1] The white paper to the development of China′s information security industry [R].Information Security Industry Branch of China Information Industry Chamber of Commerce,2015.

[2] Zander S,Armitage G,Branch P.A survey of covert channels and countermeasures in computer network protocols[J].IEEE Communications Surveys & Tutorials,2007,9(3):44-57.

[3] Lampson B W.A note on the confinement problem[J].Communications of the ACM,1973,16(10):613-615.

[4] Girling C G.Covert Channels in LAN′s[J].IEEE Transactions on Software Engineering,1987,13(2):292-296.

[5] Rowland C H.Covert channels in the TCP/IP protocol suite[J].First Monday,1997,2(5):32-48.

[6] Yu Chi,Huang Liu-sheng,Yang Wei,et al. A 3G speech data hiding method based on pitch period[J]. Journal of Chinese Computer Systems,2012,33(7):1445-1449

[7] Wang Jian-feng,Huang Liu-sheng,Tian Miao-miao,et al.Detection of HTML steganography based on statistics and SVM classification[J].Journal of Chinese Computer Systems,2014,35(6):1221-1225.

[8] Padlipsky M A,Snow D W,Karger P A.Limitations of end-to-end encryption in secure computer networks[R].Mitre Corp Bedford MA,1978.

[9] Cabuk S,Brodley C E,Shields C.IP covert timing channels:design and detection[C].Proceedings of the 11th ACM Conference on Computer and Communications Security,ACM,2004:178-187.

[10] Shah G,Molina A,Blaze M.Keyboards and covert channels[C].Usenix Security,2006,6:59-75.

[11] Sellke S H,Wang C C,Bagchi S,et al.TCP/IP timing channels:theory to implementation[C].International Conference on Computer Communications(INFOCOM′09),2009:2204-2212.

[12] Gianvecchio S,Wang H,Wijesekera D,et al.Model-based covert timing channels:automated modeling and evasion[C].International Workshop on Recent Advances in Intrusion Detection,Springer Berlin Heidelberg,2008:211-230.

[13] Huffman D A.A method for the construction of minimum-redundancy codes[J].Proceedings of the IRE,1952,40(9):1098-1101.

[14] Qiu L,Zhang Y,Wang F,et al.Trusted computer system evaluation criteria[C].National Computer Security Center(CSRC),1985.

[15] Cover T M,Thomas J A.Elements of information theory[M].John Wiley & Sons,2012.

[16] Papoulis A.Probability &statistics[M].Englewood Cliffs:Prentice-Hall,1990.

[17] Gianvecchio S,Wang H.Detecting covert timing channels:an entropy-based approach[C].Proceedings of the 14th ACM Conference on Computer and Communications Security,ACM,2007:307-316.

附中文参考文献：

[1] 中国信息安全产业发展白皮书[R].中国信息产业商会信息安全产业分会,2015.

[6] 余 迟,黄刘生,杨 威,等.一种针对基音周期的 3G 信息隐藏方法[J].小型微型计算机系统,2012,33(7):1445-1449.

[7] 王剑锋,黄刘生,田苗苗,等.基于统计和 SVM 分类的网页隐秘信息检测[J].小型微型计算机系统,2014,35(6):1221-1225.