基于空间差分平滑的非相关与相干信源数估计*
陈明建,龙国庆,黄中瑞
(国防科技大学电子对抗学院,合肥 230037)
0 引言
在阵列信号处理中窄带信号的波达方向DOA估计已在雷达、声纳、无线通信、无源定位等领域有着重要应用[1-2]。传统基于波束形成、相位干涉仪等算法测角分辨率受瑞利限的限制,这使得传统的波达方向估计方法难以获得高分辨测向。为了获得超高分辨率测向,空间谱估计实现应运而生,特别是基于子空间的多信号分类法(MUSIC)[3-4]、旋转子空间不变法(ESPRIT)[5]以及子空间拟合法[6]。然而这些超高分辨的DOA估计算法应用的前提是信源数准确已知,若假定信源数目和真实的信源数不等,此时子空间类DOA估计将出现较大误差,算法性能将会降低甚至完全失效。因此,信源数目准确估计是基于子空间类谱估计算法需要解决的关键问题。
典型的信源数估计方法包括基于AIC准则[7]和MDL准则[8-9]的信息论方法、基于特征值一步预测法[10]、贝叶斯预测密度法[11]以及 Bootstrap 法[12]等。这些方法均假定信源是不相关或者独立的,若空间信源存在一定的相关性或者完全相干时,此时数据协方差矩阵将会出现缺秩,造成信号子空间的向量泄露到噪声子空间,导致算法性能下降甚至失效。为了解决相干信源数估计问题,学者们提出了很多算法,一般可分为两大类:一类是空间平滑类算法,主要包括前向空间平滑算法[13]、前后向空间平滑算法[14-16]以及空间差分平滑算法[17-20]。空间平滑类算法主要思想是将等距线阵分成若干个相互重叠的子阵,通过对子阵的数据协方差矩阵平滑实现去相干的目的。其中前向空间平滑、前后向空间平滑算法可以分别实现个相干信源估计(M为均匀线阵的阵元数,符号表示向下取整)。空间平滑算法是以牺牲有效的阵元来恢复相干信号协方差矩阵的秩,而且无法区分相干和非相干源数目,因此,估计最大信源数不超过阵元数目。空间差分平滑算法将阵列协方差矩阵分为Toeplize部分和非Toeplize部分,利用差分运算得只含相干信源的协方差矩阵,提高了算法对信源的过载能力,但文中没有讨论非相关信源数估计问题。另一类是矩阵重构法,包括Toeplize矩阵重构算法[21-22]、ESPRIT-Like算法等[23-24],均是利用矩阵重构方式解相干。但该类方法需要牺牲一半的阵元恢复数据协方差矩阵的秩,估计信源数有限。
针对非相关信源与相干信源共存时信源数估计问题,提出了一种新的基于空间差分平滑的信源数估计算法。该方法首先利用SORTE法估计相互独立信源个数,并结合非相关信源导向矢量、相干信源阵列导向矢量矩阵分布与噪声子空间正交特性的差异,根据DOA估计结果得到非相关信源数估计,然后通过空间差分平滑剔除非相关信源信息,得到只含有相干信源信息的空间平滑差分矩阵,最后利用SORTE法实现相干信源数估计。
1 信号模型
假设K个远场窄带目标信号入射到M元均匀线阵上,阵元间距为半波长。不失一般性,假定前Ku个信源是非相关的,以角度θk入射,信号波形为sk(t),功率为,其他的信源为D组Kc个相干信源,且相干信源组彼此相互统计独立,信号波形为,功率为。第d组相干信源包含了Kd个多径信号,即满足。假定独立信号组彼此相互统计独立,则阵列接收信号可表示为
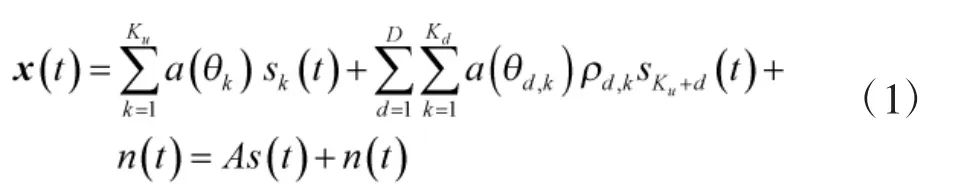
其中,a(θ)是均匀线阵阵列导向矢量,可表示为


2 信源数估计
2.1 非相关信源数估计
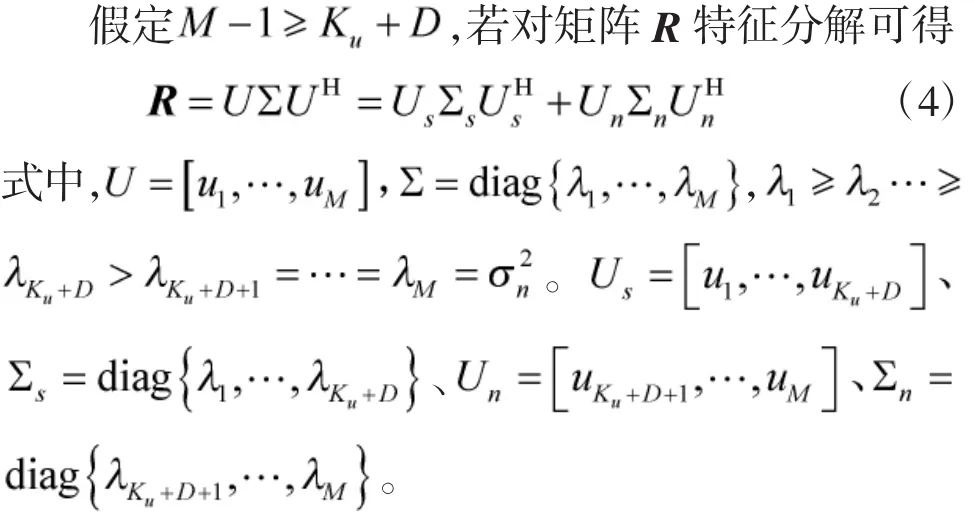
SORTE信源估计法主要思想是利用特征值二阶统计量方差信息构造信源数估计判决函数。若定义,则
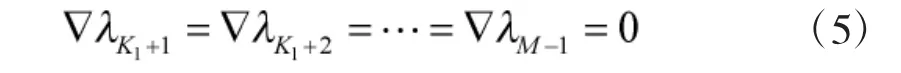
定义特征值的方差为δk
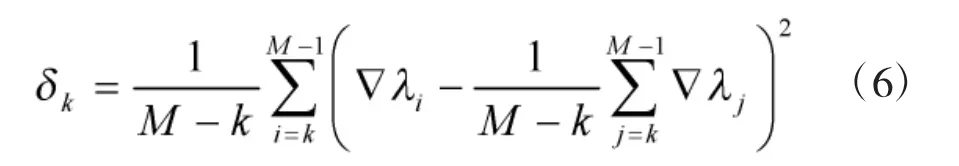
定义SORTE函数为[9]

由式(7)可知,SORTE函数满足如下关系

则独立信号(非相关信号与相干信号组之和)信源估计的判决函数为

由于Us的列向量张成信号子空间,即非相关信源与相干信源导数矢量矩阵列向量张成同一空间,由于信号子空间正交于Un的列向量张成噪声子空间,因此
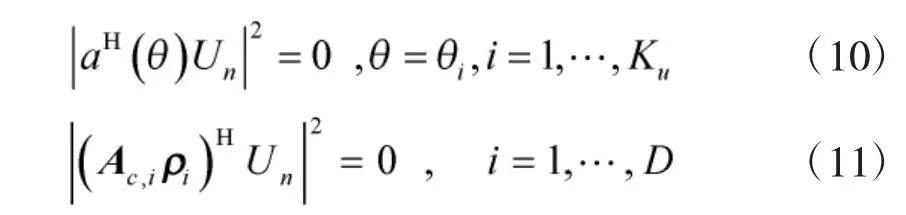
由式(11)可知,相干信源的导向矢量矩阵 Ac,iρi为范德蒙矩阵列向量的线性组合,因此,无法等价为某个方向对应的导向矢量a(θ),即利用DOA估计结果可实现非相关信源数估计。
2.2 相关信源数估计
2.2.1 传统的空间平滑算法
1)前后向空间平滑算法。空间平滑算法利用均匀线阵的平移不变性,将阵列划分为相互重叠的p个子阵,其中每个子阵包含有相同的阵元数M-p+1。前向空间平滑算法是分别计算p个子阵的协方差矩阵,再求算术平均,可得等效M-p+1阶子阵列协方差矩阵为

前后向空间平滑算法是同时对阵列前后向进行平滑得到阵列协方差矩阵为
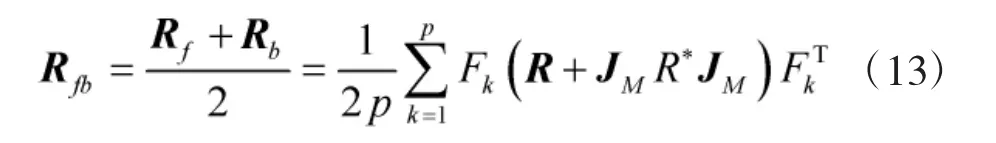
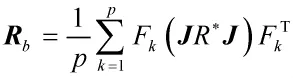
通过FSS、FBSS空间平滑后,阵列数据协方差恢复为满秩,此时可以利用信息论的AIC、MDL等方法即可实现相干信源数估计。
2)空间差分平滑算法。空间差分矩阵定义为
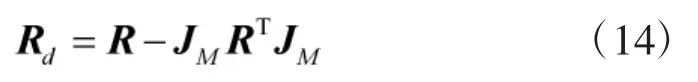
考虑非相关信号协方差矩阵RN为Toeplitz矩阵,且满足,则将式(3)代入到式(14)可得
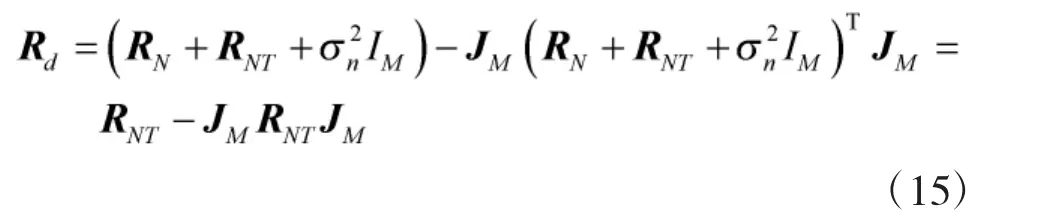
由式(15)可知,空间差分矩阵中不含非相关信源信息,然后利用式(12)对式(15)进行前向平滑可得
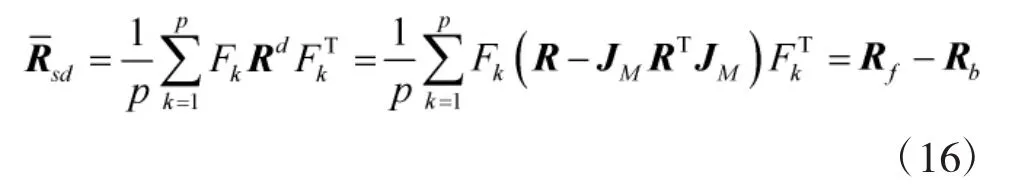
由式(16)可知,空间差分平滑算法本质上是前后向平滑差分算法。
2.2.2 本文算法
假定将均匀线阵划分为相互重叠的p个子阵,则第k个子阵的阵列数据协方差矩阵为

定义:对于M×M维矩阵R,空间差分平滑矩阵为

若非相关信源和相干信源同时入射ULA阵列,则Rsd不含有非相关信源信息。
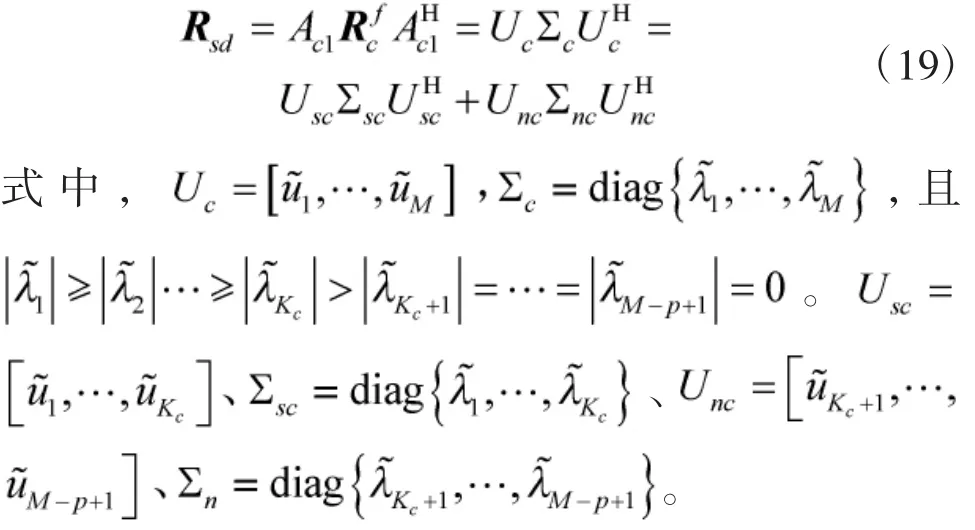
利用Rsd特征值的绝对值的方差信息,通过SORTE法实现相干信源数估计。
综上所述,本文算法基本步骤可以归纳如下:
2)利用式(11)非相关信源DOA估计关系式,从而得到非相关信源数和相干信源组数估计;
3)利用式(18)计算空间差分平滑矩阵Rsd;
4)对Rsd特征分解得到特征值的绝对值,利用SORTE算法估计相干信号信源数。
2.3 阵元需求分析
假定有K个窄带信号以平面波入射ULA,其中非相关信源数为Ku,D组相干信源总数为Kc,其中相干信源组中最多含有信源数为Kmax。若要成功分辨所有入射信号,对于FSS、FBSS、SDS算法需要阵元数分别为、,本文算法需要阵元数为,由以上分析可知,FSS算法对阵元需求最高,阵列自由度损失最大,FBSS算法阵列需求小于FSS算法。本文算法所需阵元数最少,SDS算法性能次之。
3 仿真实验
实验1一组相干信源时成功检测概率与SNR、快拍数关系。考虑均匀线阵阵元数M=11,阵元间距为半波长。其中3个非相关信号和1组4个相干窄带信号同时入射到阵列上,非相关信号DOA分别为[-21°3°35°],相干信号 DOA 分别为[-41°-19°5°38°],假定入射信号均为等功率信号,其功率为,阵元噪声为理想的高斯白噪声。信噪比定义为。采样快拍数为100,Monte Carlo实验次数为100。定义成功检测概率为正确估计信源次数与实验次数之比。图1是采样快拍数为100时成功检测概率与SNR关系曲线。图2是SNR为10 dB时成功检测概率与快拍数关系曲线。

图1 单组相干信源时成功检测概率与SNR关系
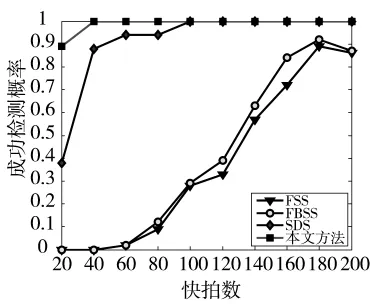
图2 单组相干信源时成功检测概率与快拍数关系
由前文分析可知,当Ku=2,Kc=4时,此时FSS、FBSS、SDS以及本文方法所需最少阵元数分别为10、8、7、6。理论分析可知当 M=11时,4 种算法均能实现信源数估计,这与图1、图2实验结果相吻合。其中FBSS算法性能略优于FSS算法,SDS算法和本文算法均采用空间差分平滑技术消除了噪声,相当于提高了SNR,因此,性能优于传统的空间平滑算法,且本文算法性能更好。
实验2信源角度相近时成功检测概率与SNR、快拍数关系。若假定非相关信号DOA分别为[-12°-3°45°],相干信号 DOA 分别为[-11°-2°30°44°],其他仿真参数不变。图1是采样快拍数为100时成功检测概率与SNR关系曲线。图2是SNR为0 dB时成功检测概率与快拍数关系曲线。
由下页图3、图4可以看出,非相干信源均与相干信源角度间距很近,此时导向矢量矩阵列向量存在相关性,传统FSS、FBSS算法通过空间平滑后数据协方差矩阵仍然可能是缺秩,因此,无法正确分辨角度相近的信源,而本文算法和SDS通过空间差分平滑,将非相关信源与相干信源分开分辨,因此,分辨性能不受角度间隔的影响。

图3 信源角度相近时成功检测概率与SNR关系
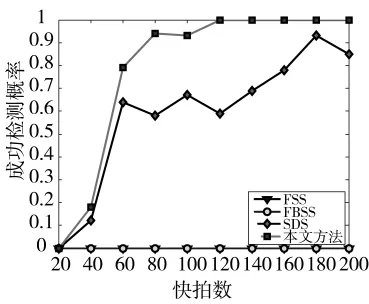
图4 信源角度相近时成功检测概率与快拍数关系
实验3多组相干信源时成功检测概率与SNR关系。假定M=8,共有6个远场窄带信号,其中2个非相关信号DOA分别为[-20°10°],2组4个相干信号DOA分别为[-40°0°20°30°]。其他仿真参数同实验1。图5是快拍数为200时成功检测概率与SNR关系曲线;图6是SNR为5 dB时成功检测概率与快拍数关系曲线。

图5 两组相干信源时成功检测概率与SNR关系
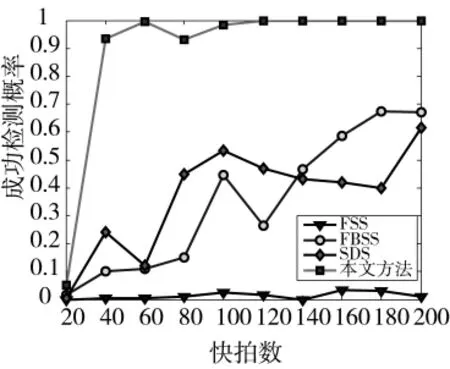
图6 两组相干信源时成功检测概率与快拍数关系

图7 信源数超过阵元数时成功检测概率与SNR关系
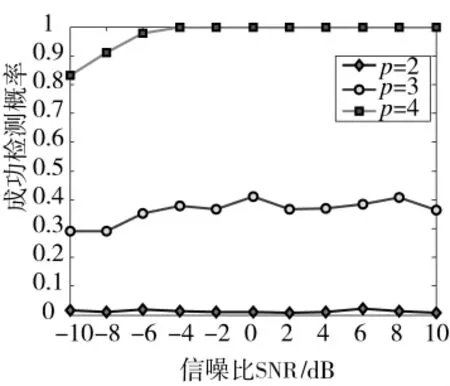
图8 不同子阵数时成功检测概率与SNR关系
由图5、图6可知,当SNR大于15 dB时4种算法均能实现信源数一致估计;在SNR小于5 dB时,由于SDS算法采用空间差分消除了高斯白噪声,因此,SDS算法性能优于FBSS算法,但SNR大于5 dB时,其SNR的优势不再明显,此时FBSS性能优于SDS。FSS算法由于有一半的阵列孔径损失,因此,其性能最差,而本文算法性能最优。
实验4信源数超过阵元数时成功检测概率与SNR关系。假定M=8,共有10个远场窄带信号,其中4个非相关信号DOA分别为[-40°-20°-10°0°],3组 6个相干信号 DOA 分别为[-30°-10°0°20°40° 60°]。其他仿真参数同实验3。图7是信源数超过阵元数时成功检测概率与SNR关系曲线。
当 M=8,K=10 时 FSS、FBSS、SDS 以及本文算法可检测信号个数分别为 8、9、8、7、10。因此,理论上FSS、FBSS、SDS算法均失效,只有本文算法能够有效检测10个入射信号,图7的仿真结果与理论分析相一致。
实验5子阵数对成功检测概率的影响。假定M=8,2组4个远场窄带相干信号DOA分别为[-30°-10°15°20°]。其他仿真参数同实验 1。图8是不同子阵数时成功检测概率与SNR关系曲线。
由理论分析可知:当只有相干信号入射时,由于对数据协方差矩阵进行了空间差分平滑,对消了高斯白噪声,因此,检测性能基本不受噪声的影响,这与图8实验结果相吻合;当子阵数p在满足不等式时,空间差分平滑后的协方差矩阵恢复为满秩矩阵,即可实现对相干信源数估计。不同的子阵数p对本文算法的检测性能有一定影响,若p越大算法信源检测性能越优。
4 结论
针对非相关和相干信源共存时信源数估计问题,本文提出了一种新的空间差分平滑算法。首先利用SORTE法估计得到非相关信源和相干信源组数的联合估计,然后通过空间差分平滑实现相干信源数估计。相比其他类算法,本文算法具有如下优点:1)将非相关信源和相干信源分开检测,提高了算法对信源检测能力,当阵元数超过6时,可检测信源数可以超过阵元数;2)可以分辨到达角相近的信源;3)空间差分平滑剔除了高斯白噪声,且适用于更广泛的Toeplitz类色噪声,改善了算法在低信噪比时信源数检测性能。

