基于可视化HPSO的无人机装备维修任务调度*
沈延安,叶 霖
(陆军炮兵防空兵学院,合肥 230031)
0 引言
军用无人机是信息化高技术条件下具有高效费比、攻防兼备的新概念装备,可用于目标指示、侦查校射、电子干扰、火力打击等多种用途,目前已在各军种得到广泛应用。由于无人机系统[1]装备组成复杂,备件类型多,且维修地点随无人机分队的任务机动实时变化,导致其装备维修任务的路径选择[2-4]由时间、距离、地形、任务类别等诸条件决定,并视战场环境适时调整,容易形成复杂的NP(Non-deterministic Polynomial,NP)问题,加大了无人机装备维修保障任务的工作难度。
快速、准确的维修任务调度不仅能够节省维修费用及时间,更能够提高装备的作战效能,具有重要的研究意义。文献[5]提出维修点重要度和资源保障度的概念,研究了战时装备维修资源的优化调度;文献[6]采用并行过程的二阶段非均匀紧急任务列表,解决了非均匀环境下的任务调度问题;文献[7]采用混合内核仿真解决了非专用计算环境下的任务调配问题,虽然能够解决特定环境下的任务规划,但不能满足军用无人机装备维修的特殊需求,且算法过程不够自动化、智能化。
混合粒子群优化算法(Hybrid Particle Swarm Optimization,HPSO)是粒子群算法[8]的改进,具有参数设置灵活、收敛速度快、鲁棒性好等特点,目前已被广泛应用于各类工程实践。董颖[9]较早进行了HPSO 方面的研究;陈汉武[10]、陈喜阳[11]分别将粒子群算法与遗传算法、神经网络相结合,拓展了HPSO 的应用领域;田军[12]、叶文[13]、武善玉[14]等进一步采用离散化HPSO简化编/解码过程,解决了复杂条件下的任务调度问题,但对迭代过程的粒子的分布及运动特点不够关注,使计算过程易陷入局部最优,限制进化速度。本文在离散化HPSO的基础上,建立了以粒子邻接距离为依据的浓度监控机制,结合动态图像展示函数,实现可视的种群进化调控,利用改进的HPSO算法对无人机维修任务调度进行科学的决策支持。
1 无人机装备维修任务调度问题系统分析
无人机装备维修任务调度主要通过对维修任务进行计划、协调和控制,实现维修资源的合理调配和使用,提高装备保障的响应效率,力求以最短的时间,最少的消耗,获得满意的保障效果。
统观目前军用无人机系统,其维修保障任务从功能组成上讲基本相同,相关维修任务具有以下普遍特征:1)装备组成复杂,部件精密,维修技术需求较高;2)机动性强,为保证侦查校射和目标打击的精度要求,需要实施大量的战术机动,导致装备维修任务在不同时间、不同任务阶段实时动态变化。结合霍尔三维结构分析,明确无人机装备维修任务调度问题的组成要素,如表1所示。

表1 无人机维修任务调度组成要素
因此,无人机维修任务调度需要随时根据故障类型、任务分布及库存情况,制定优化方案,其规划空间维数较高、约束条件多、指标模糊性大,随着维修站点及任务数量的增加,调度方案数量将急剧增长。针对这一典型的NP问题,传统的枚举法、图论、线性规划等方法已不再适用。本文通过改进的HPSO算法,针对该问题进行具体研究。
2 维修任务调度问题的数学描述
假设每一个特定规模的作战区域中各有一个无人机维修保障中心,拥有K个维修保障分队,将各维修保障分队的备件储备最大任务载荷定义为综合服务能力,记为Qk(k=1,2,…,K);同时有L个维修任务点的维修任务需要完成,各维修任务点的备件需求量为Ni(i=1,2,…,L),且max{Ni}<max{Qk};将各维修站点编号为0,1,…,L,其中,以M0为无人机维修保障中心,M1,M2,…,ML为维修任务点。另定义变量如下:

设cij为任务点i到任务点j的任务成本,其可用的含义包括运输费用、机动距离和行驶时间等。由于军队装备保障的特殊需求,首先应保证响应维修任务的时效性,考虑到维修站点位置实时动态变化、且装备保障分队的最大机动速度相对固定,因此,本文将cij定义为任务行驶时间。rk为目标函数的固有成本,这里定义为固有维修时间。
对维修任务实施过程提出以下基本假设与约束条件:
1)各维修分队负责站点的维修资源需求总和小于维修分队的任务最大载荷,即一次任务调度路线中不存在中途返回;
2)各维修站点有且仅有一个维修分队负责,即不存在维修站点接受多方服务;
3)各维修分队的任务调度路线中途经的维修站点均为其负责对象,即维修分队在任务响应过程中仅途经其任务站点。
若以Z为全体维修保障分队的任务完成时间(Mission Finished Time,MFT),且以该时间最短作为维修任务优化调度的系统目标,则无人机装备维修任务调度的数学模型为:
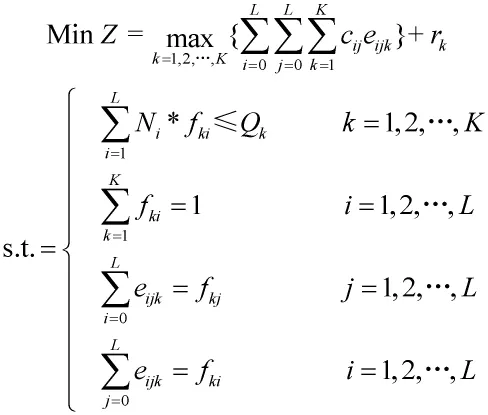
3 可视化HPSO算法设计
3.1 粒子群算法基本原理
粒子群算法是 Eberhart和 Kennedy[4]于 1995年提出一种基于集群智能的进化类算法,其基本思想是基于生物的集群信息共享机制,以每个粒子的位置代表一个解的状态,以适应度函数作为解的优劣的评价标准,由粒子的个体历史最优位置Pi和集群全局最优位置Pg共同决定粒子的运动方向,并通过迭代计算对粒子群进行更新,直到获得满意的计算结果。
设指标空间为D维,总粒子数为n。第i个粒子位置表示为向量 Xi=( xi1,xi2,…,xiD);第 i个粒子运动历史中的最优位置为 Pi=( pi1,pi2,…,piD),其中第g个粒子的过去最优位置Pg为所有Pi(i=1,…,n)中的最优;第 i个粒子的速度为向量 Vi=(vi1,vi2,…,viD)。每个粒子的位置和速度按迭代公式如下:

其中,c1,c2为学习因子;w称惯性因子,定义为粒子的动态惯性步长,用于实现迭代过程自适应步长调节,wmax和wmin是w的最大、最小值;iter和itermax分别是当前迭代次数和最大迭代次数;rand()为[0,1]之间的随机数;粒子第 d(1≤d≤D)维的位置变化范围为[-XMAX-d,XMAX-d],速度变化范围为[-VMAX-d,VMAX-d],若迭代过程中粒子运动状态超出边界,则以边界赋值。
3.2 粒子编码/解码方法
本文以四维粒子结构对维修任务进行描述,粒子的第1维度x1采用自然码编码方式来表征L个维修任务站点;第2维度x2以随机数的形式映射各维修任务站点分配的维修分队;第3维度x3代表对应任务站点的维修资源需求量Ni;第4维度x4为维修站点的空间坐标Wi。由此得出模型中一个完整的粒子编码形式为:

表2 粒子编码形式
按照编码格式对粒子x2进行取整,得到1~K的随机序列,实现将各站点的维修任务映射到K个维修分队中,完成粒子的初始化。
维修任务调度的粒子解码过程为:
1)根据维修站点的责任划分,归纳各维修分队对应的任务链集合 M1{},M2{},…,Mk{};
2)读取各任务链集合当中粒子当前站点Ti1,Ti2,…,Tik;
3)由第4维度x4计算粒子当前站点到集合内剩余维修站点的运输成本cij(任务行驶时间),并按由小到大顺利排序;
4)选取各任务链集合中cij数值最小的维修站点 Ti1′,Ti2′,…,Tik′,计算响应后累计消耗备件数量Ni′;
5)若 Ni′<Qi(累计备件消耗未超过最大载荷),则执行步骤6),否则跳转步骤2);
6)更新粒子当前站点 Ti1′,Ti2′,…,Tik′,计算粒子适应度Z,确定维修分队的机动方向;
7)逐次计算,始终保证维修分队按照最小运输成本原则进行机动,直到遍历集合内责任站点,完成初始化粒子的解码。
3.3 HPSO算法改进
3.3.1 离散粒子群
由于粒子的编解码过程中,x1,x3,x4均为辅助变量,而决定粒子优劣的主要因素为维修任务点的分配情况,即x2。为了构造初始化整数序列,粒子在迭代过程中针对随机变量x2涉及大量的取整运算,影响计算效率,因此,可对粒子参数x2进行离散处理,使之更适合解决本文的研究问题。
本文采用Sigmoid函数来映射参数s,通过s(t)将迭代过程中每一个粒子中xi2的值编码为1~K以内的整数序列,即:

设ρ为[0,1]区间内的随机数,则针对参数x2构造的二进制离散粒子群算法的粒子速度和位置的更新公式为:

式(5)中,ceil[]和round[]分别代表向上取整运算与就近取整运算,考虑映射算子s(t)与vi2(t)为正相关关系,且粒子进化差距越大,对移动步长需求越大,可根据粒子位置,通过合理选择取整方向控制移动距离,实现任务序列的粒子离散化处理。
3.3.2 粒子浓度监控机制
传统粒子群算法的迭代机制使得粒子在后期的相似度较高,易陷入局部最优。本文引入粒子浓度监控机制,综合了粒子浓度和适应度两方面信息,对粒子群的进化过程进行调控。
定义粒子浓度Ck为种群中在当前粒子邻接分布的粒子个数与种群规模之比,即Ck=Nk/N。邻接分布的数学意义为两粒子间的平均距离小于一个VMAX-d,本文通过欧式距离对粒子的距离进行计算,将两粒子间的平均距离表示为:
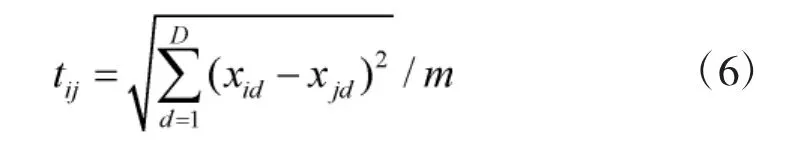
浓度监控机制主要根据粒子的分布情况,实时地对粒子适应度进行调整,具体通过构造空间适应度Z′来实现:

其中,Zk′为空间适应度,Zk为原粒子适应度。由于Zk′与Zk成正相关,与Ck成负相关,以空间适应度表征粒子的质量优劣,即可实现对高浓度粒子进行抑制,对浓度低、适应度大的粒子促进。
3.3.3 粒子定向交叉遗传
引入遗传算法的思想,当粒子陷入集中分布,且解质量较低时,根据粒子浓度选择种群中适应度高而浓度较低的粒子进行交叉、变异,使粒子跳出局部极值,加快进化过程。
根据粒子空间适应度,采用轮盘赌的方式选择参与子代遗传的粒子,选择概率为:

遗传过程采用实数交叉操作来实现信息交换,交叉过程如下:

粒子的变异过程通过随机选择变异粒子中的第d维为变异点,随机产生初始速度:

为了确保变异粒子的局部的随机搜索能力,避免粒子接近最优解的趋势因变异遭到破坏,变异概率应取小值,因此,本文中变异概率取0.1。
3.3.4 可视化处理
针对传统粒子群算法仿真动态过程反映不直观的问题[15],本文基于Matlab粒子群工具箱PSOt,通过GUI模块优化了用户界面,改进了图形展示函数goplotpso.m,能够实时展现粒子在迭代过程中的空间分布与参数状态,其基本调用方式为:
pso_Trelea_vectorized (′main_func′,n,Max_V,range,minmax,Pdef)。其中,Pdef=[me,ps,ac1,ac2,iw1,iw2,iwe,ergrd,ergrde,errgoa,trelea,PSOseed],代表算法的参数设置,主要包括画面记录步长、进化代数、群体规模、学习因子、惯性因子、约束条件、中止迭代条件、初始化状态等参数信息。
4 实例分析
以某次无人机[16]分队山地作战维修保障任务为例,作战区域内含有一个维修保障中心L0,坐标为(11.62,5.23,0),以 km 为单位;另有 10 个维修任务点L1~L10,各无人机分队根据任务需要实时机动,某时刻各维修任务点的空间分布如图1所示。

图1 维修中心与任务点空间分布
设维修保障中心拥有4个维修保障分队,各维修保障分队的综合服务能力均为40,最大机动速度为90 km/h,固有维修时间计0.56 h,各维修任务点的资源需求量依次为 {7,5,3,6,6,8,2,7,11,9},且位置坐标为已知,如表3所示。

表3 维修任务点位置坐标
在Matlab 2015b环境下运行混合粒子群程序,相关参数设置为:画面展示步长为1,学习因子c1=c2=2,惯性因子 wmax=0.9、wmin=0.4,种群规模、进化代数均为30,迭代终止精度要求为1e-25,粒子速度设置vmax=5、vmax=-5,以MFT最短作为寻优目标,迭代过程如图2所示。
连续进行40次仿真计算,对结果进行统计,并与普通粒子群算法进行对比,将两种算法得到最优结果展示,如图3、图4所示。
根据实验统计,进一步对两种算法的达优次数、达优率、平均计算时间等性能指标进行列举,如表4所示。
通过对比可知,在40次模拟实验中,混合粒子群算法的寻优能力明显高于普通粒子群算法,且具有解质量高、迭代速度快等优点,而普通粒子群算法易陷入局部最优解、计算结果不够稳定。

图2 改进的HPSO算法流程
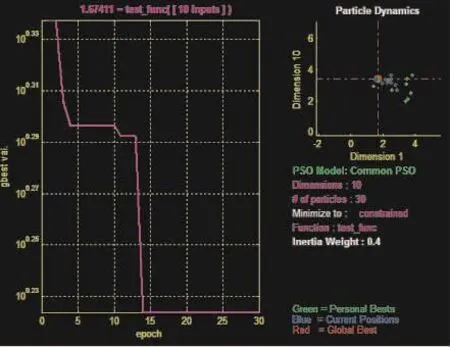
图3 普通粒子群算法最优结果

图4 改进的HPSO最优结果

表4 主要性能参数比较
综上,采用混合粒子群算法得出最优结果,查询相应维修保障分队的任务点分配、调度次序、机动距离、任务时间等信息,得出该任务背景下的最优调度方案。
各维修保障分队同时从保障中心出发,K1分队经L9到达L6,K2分队经 L1到达 L2,K3分队经L4、L5、L7 到达 L3,K4 分队经 L10 到达 L8,维修任务展开1.617 h后,作战区域中所有无人机分队的维修需求得到满足,即最优任务完成时间为1.617 h。

表5 最优调度方案
5 结论
本文针对军用无人机装备维修任务调度的特殊需求,对传统粒子群算法进行了改进,采用离散化粒子群简化粒子论域,加快计算速度,引入浓度监控机制对粒子的分布及运动过程进行调控,并通过粒子交叉遗传加快进化速度,防止陷入局部最优。通过实例分析表明,改进的混合粒子群算法能够进行高效仿真计算,快速得出维修任务最佳调度方案,且解质量更高、迭代速度更快,进化过程更加直观,证明了混合粒子群算法在装备资源调度问题中的有效应用,为军队维修保障的决策工作提供了新的思路。

