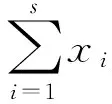卡塔兰数及其在竞赛中的应用*

●

(绍兴市第一中学,浙江 绍兴 312000)

1 卡塔兰数的介绍

卡塔兰数列是组合数学中一个重要的数列，这个数由比利时的数学家卡塔兰命名，它常常出现在各种计数问题中,并在竞赛数学中有着广泛的应用.它的一般项为

(1)

它的前几项为

C0=1，C1=1，C2=2，C3=5，C4=14，C5=42，C6=132，C7=429，C8=1 430，C9=4 862，C10=16 796,……

本文首先给出对应卡塔兰数的两个组合问题，或者称它的定义.不同的文献会给出不同的定义[1]，我们后面还会给出它的其他等价形式，即卡塔兰数在竞赛中的应用.

问题1卡塔兰数是研究由n个+1和n个-1组成的所有序列x1,x2,…,x2n中，满足条件

x1+…+xk≥0,其中k=1,2,…,2n(2)

的序列数目.条件(2)的意思形象地说，就是在这个序列中，从左到右的任何位置及之前的位置中，数字+1出现次数不会比数字-1出现的少.

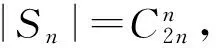
σ=(-x1)…(-xk0)xk0+1…x2n，

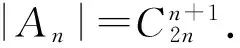
问题2证明：在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数就是卡塔兰数Cn.

分析设所求方法数目是Dn，我们记y1,y2,…,y2n是圆周上依次按顺时针排列的2n个点.若y1与yk相连，且能把其余点成对连接起来使得线段不相交，则k=2m必须是偶数，于是把问题转化成y1,y2,…,yk-1,yk和yk,…y2n-1,y2n这两个部分的对应成对连接而不相交的问题，方法数依次是Dm和Dn-1-m，对m=0,1,…,n-1求和

其中D0=1.

图1

下面说明问题1的方法数Cn和问题2的方法数Dn是相等的.事实上，对于任意一个n个+1和n个-1的序列y1,y2,…,y2n，对从左到右的第一个-1及它前面的最近的一个+1，联结这两个点，然后在删掉这两点的序列中，重复上述过程，就得到n对不相交的连线.图1是n=4的情形，对应序列是

(+1)(-1)(+1)(+1)(-1)(-1)(+1)(-1),

且这样的对应是一一的，即Cn=Dn，从而也证明卡塔兰数Cn满足C0=1,且

(3)

许多不同形式的问题，本质上都等价于上面的基本问题，我们有时直接求得式(1)，有时导出递推关系式(3)来求得卡塔兰数.

2 卡塔兰数不同形式的应用

前面给出了卡塔兰数两种不同的问题形式.下面来介绍一下卡塔兰数在国内外数学竞赛中的应用，有些例题是比较显然的应用[2]，有些需要对问题进行等价转化，才能利用卡塔兰数.但事实上利用卡塔兰数的原理，一些很复杂的问题都可以迎刃而解.

例1在O-xy平面的单位长度的网格线上行走，从始点(0,0)走2n步到终点(n,n)，每步只能往右或向上行走1单位长度，求满足条件y≤x的路径数？

分析只要把向右一步记作+1，向上一步记作-1，这和问题1是等价的.注意到：若条件y≤x替换成y

例2在2×n的表格中填入数字1，2,…,2n，求每行、每列的数字是升序排列的方案数.

分析用n个+1和n个-1排成一列σ=x1x2…x2n，若其中xi1,xi2,…,xin为+1，则表格第一行的数为i1，i2，…，in，而对应-1的数依次填入第二行，这样每行的数字显然是升序.再若序列σ中从左到右，数字+1的数目大于等于-1的数目，即满足式(2)，则表格中每列的数字也是升序.反之，将数字1,2,…,2n填入2×n的表格中，第一行的数字i对应xi=±1，而第二行的数字j对应的xj=-1，于是每行、每列的数字是升序排列所得到的序列σ=x1x2…x2n满足式(2).

例3求方程x1+x2+…+xn=n的非负整数解的个数，要求满足

x1+…+xk≥k,其中1≤k≤n.

分析将每组解中的xi变换为11…10(其中xi个1，1个0，若xi是0则不变)，依次连在一起，会产生n个1和n个0的序列.例如n=3的一个解x1=1，x2=2,x3=0,则对应序列101100.我们可以看出，这样的序列从左到右的任何位置，1的个数比0的个数多.如果数字0用-1来代替，则等价于问题1.于是原方程的非负整数解的个数就是卡塔兰数.

例4设n+1个元素相乘，P=a0×a1×…×an，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

分析可以导出和式(3)相同的递推关系.事实上，设括号化的方案数目为Dn，考虑n个乘法中最后一个运算的乘法来分类计数.若最后一个乘法是第k个，则前面由k-1个乘法，它的数目是Dk-1；而后面有n-k个乘法，数目是Dn-k.取遍k=1，2，…，n，定义D0=1，于是

这就是递推关系(3)，从而Dn=Cn.

例5求一个凸n+2边形区域划分成三角形区域的方法个数.

分析设凸n+2边形区域划分成三角形区域的方法数为Dn，记D0=1.设凸n+2边形的顶点按顺时针方向依次记为x1，x2…，xn+2.若x1xn+2是划分的其中一个三角形的一条边，设另一顶点是xk(其中k=2，3，…,n+1)，即3个顶点x1，xk，xn+2是其中的一个三角形区域，则凸n+2边形分成两部分，凸k边形和凸n+2-k边形，于是

同样得出递推关系式(3)，也即Dn=Cn.

例6求用n个长方形填充一个高度为n的阶梯状图形的方法个数.

分析首先看到用n个长方形填充一个高度为n的阶梯状图形时，任何两个矩形都不能合并成一个矩形.当n=3时，如图2，所求的方法数是5.

图2

图3

对于一般的n，若记所求为Dn，规定D0=1，则当右下角是k×(n-k+1)时，如图3，右边剩下的是高为k-1的阶梯状图形，上边剩下的是高为n-k的阶梯状图形.对k=1，2，3，…,n+1递推计数求和,得

同样得出递推关系式(3)，也即Dn=Cn.

例7某班的男生和女生人数相同(全班人数不少于4人),将他们以各种不同的方式排成一行,看看能否将这一行分成两部分,使得在每一部分中,男生和女生都各占一半,设不能这样分开的排法种数为a,恰有一种方法可以这样分开的排法的种数为b.求证:b=2a.

(1972年匈牙利数学奥林匹克竞赛试题第2题)

分析任取一种排队方式,若从左到右第i个人为男生,记xi=+1,否则记xi=-1,得序列x1x2…x2n.若能将队列分为两部分,使两边男女各占一半,则存在i使得

x1+x2+…+xi=0,

xi+1+xi+2+…+x2n=0,

x1+x2+…+xi=0,

xi+1+xi+2+…+x2n=0,

例8设数列{cn}定义如下:c0=1,c2n+1=cn(其中n≥0),c2n=cn+cn-2en(其中n>0),en是满足2en|n的最大非负整数.证明:

(2011年美国国家队选拔题第5题)

分析由于要证明的等式的右边是第n+1个卡塔兰数,因此,其就是n+1对括号排成一行的所有可能数.

对于某一个关于括号的排列,设其标号为k是二进制的n位数,k从左到右的第r个数码为0或1取决于关于括号的排列从左到右的第2r+1个括号是闭(即“)”),还是开(即“(”).

设dk是所有标号为k的n+1对括号的排列数目,事实上dk与n无关.在二进制表示的k前面加一个0,相当于在关于括号的排列的第1个开括号的后面插入一对形如()的括号.故只需证明:ck=dk(其中k=0,1,…,2n-1).

对于任意的n,d0=c0=1.这是由于标号为0的关于括号的排列只能是形如:(()()…()).接下来只需证明:dk和ck满足同样的递归式.

若关于括号排列的标号为2k+1,则其末位数为1,于是关于括号排列的最后一定是().从而,关于n+1对括号且标号为2k+1的所有排列的数目就等于关于n对括号且标号为k的所有排列的数目,即d2k+1=dk(因为dk与n无关).

考虑关于n+1对括号且标号为2k的排列.设2ek|k,则k在二进制表示下末尾恰有ek个0.于是第2n-2ek-1个位置上是开括号.

1)若其右边紧接着是一个闭括号，将两个括号作为一对括号从这个排列中去掉，剩下的关于n对括号的排列的标号为k-2ek；

2)若第2n-2ek个位置上是开括号，它可以与其右边紧接着的一个闭括号(因为2k在二进制表示下末尾恰有ek+1个0)作为一对括号从这个排列中去掉，剩下的关于n对括号的排列的标号为k.

因为以上两种情形均可逆，所以

d2k=dk+dk-2ek.

由于dk,ck有相同的初始值，且由递归式唯一确定，故对于所有的整数k≥0，有dk=ck.

[1] 单墫．数学奥林匹克命题人讲座——集合与对应[M]．上海：上海科技教育出版社，2009.

[2] 张垚，冷岗松，沈文选．奥林匹克数学中的组合问题[M]．长沙：湖南师范大学出版社，2009.