浅谈圆的性质在解析几何中的应用*

●

(云和中学,浙江 云和 323600)

1 问题提出

圆是高考必考的知识点之一，有关圆的定义、性质及方程等在高考试题中常有涉及.有的试题是“显性”呈现的，求解难度不大；有的试题则是“隐性”的，需要通过挖掘题中隐含的信息，进而将其转化为与圆相关的问题[1].这类试题如果按照常规思路，往往运算繁琐，以致于难以求解，若能转化为与圆相关的问题，再借助相关性质求解，则柳暗花明，尤其是在求解解析几何问题时更是如此.

2 巧用性质，“圆”来如此

初高中以来，学生对圆的定义、性质及方程等进行了系统学习，具备了一定的应用能力.下面笔者具体阐述在求解解析几何问题时，如何将其与圆建立联系，进而利用圆的性质解决.

2.1 垂直位置关系的转化

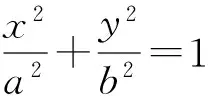
此题从代数角度运算较为复杂.由于条件具有垂直关系，可以考虑构造辅助圆来求解.

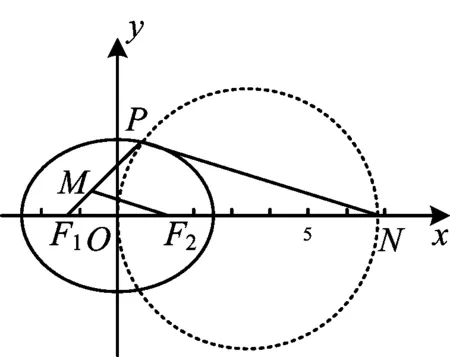
图1

分析如图1，取N(5c,0)，联结PN，得

从而

NP∥F2M.

因为PO⊥F2M,所以

PO⊥NP,

点评“直径所对的圆周角是直角，反之，直角三角形直角顶点在以斜边为直径的圆上”,借助圆的这一性质，可将垂直关系和圆建立联系，如例1中通过构造出新的垂直关系后再转化为圆求解，大大简化了计算量.

2.2 “弦长”乘积关系的转化

图2

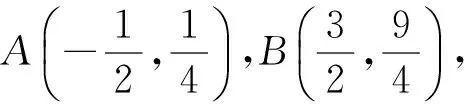
1)求直线AP斜率的取值范围；

2)求|PA|·|PQ|的最大值.

(2017年浙江省数学高考试题第21题)

若利用弦长公式求解，则运算复杂.考虑到AQ⊥BQ，点Q在以AB为直径的圆上运动，结合问题要求线段长度乘积，故可考虑利用圆幂定理求解.

分析如图3，作△ABQ的外接圆，记AB的中点为圆心R，直线PR与圆交于点M,N，由圆幂定理得

|PA|·|PQ|= |PM|·|PN|=

(r+|PR|)(r-|PR|).

图3 图4

点评圆幂定理又称相交弦定理，由于初中阶段对这一内容要求不高，因此很多学生想不到用这一性质求解例2.建议教学中可以适当补充它的应用，有利于拓宽学生的解题思路.另外，也可以借助数量积的几何意义和极化恒等式，再利用圆的性质求解：

2-|RP|2,

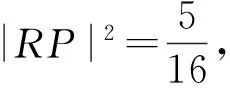
2.3 角度大小关系的转化

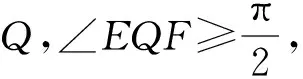
图5

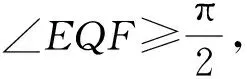
|EF|=2|MN|=2(|MC|+2)，

易知|MC|的最小值为点C到直线l的距离，从而

于是

点评顶点为动点的角度问题，借助同弧(或弦)所对圆周角相等的性质，可以发现角的顶点的轨迹和某圆有关系(圆上、圆内或圆外)，且该圆经过角的另外两个点.借助这种思路，可以发现以下结论：

结论1已知点E，F在⊙C外，点P在⊙C上运动，设⊙M经过点E，F，则有：如图6，当点P位于⊙M与⊙C的切点A处时，∠EPF最大；如图7，当点P位于⊙M与⊙C的外切点B处时，∠EPF最小.

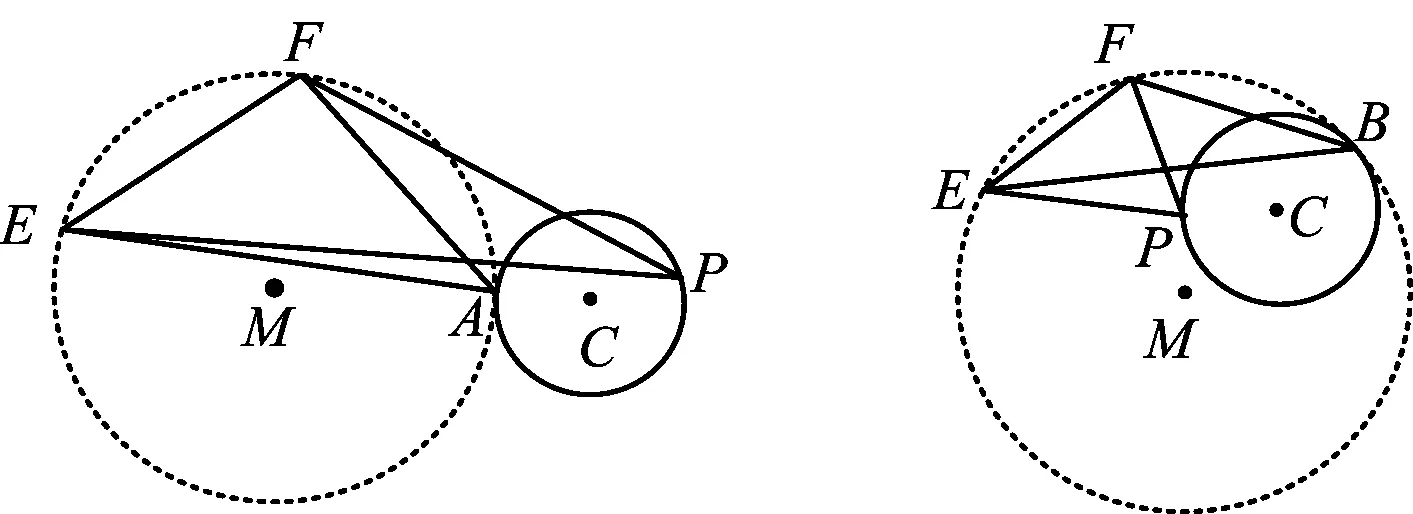
图6 图7

图8

2.4 面积最值关系的转化

常规思路是将直线l与椭圆联立、消元，再借助公式求出弦长|AC|及点O,B到直线l的距离，进而表示出四边形OABC的面积来求解，但代数运算量较大.

1)若点A,B,C共线，则点A′,B′,C′仍共线，且变换前后对应线段长的比值不变；

借助伸缩变换及以上性质，例4可以求解如下：

图9

分析如图9，利用伸缩变换

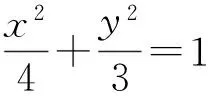
x′2+y′2=1，

即四边形OABC面积的最小值为3.

点评借助伸缩变换，将椭圆问题转化到圆中求解，再结合圆的对称性及垂径定理，可以大大简化计算.在教学中，也可以利用伸缩变换T的逆变换T-1，借助圆中一些已有的性质来发现椭圆新的性质，实现椭圆知识和圆的知识类比学习.这种用联系的观点学习数学，可以使孤立的知识点统一起来，对学生构建知识网络、提升数学思维有着重要意义.

3 问题反思

圆作为一种基本平面图形，其定义、性质及方程在解析几何中应用广泛.很多问题看似与圆无关，但如果深入寻找，往往能发现“隐性”圆的存在，进而转化为与圆相关的问题，再运用圆的性质求解，这正是化归思想在高中数学解题中的应用.

引导学生将圆化“隐”为“显”，一方面能提高学生的解题能力，特别是解析几何问题用常规思路往往运算繁琐，而化圆求解，可以大大简化运算；另一方面，可以实现不同知识点的融会贯通，有利于知识体系建构，锻炼学生的化归能力.

[1] 吴定业.化“隐”为“显”，“圆”来完“美”[J].上海中学数学，2017(7):6-7.

[2] 钟顺荣.利用伸缩变换求解直线与椭圆相切问题初探[J].中学教研(数学)，2015(3)：16-18.