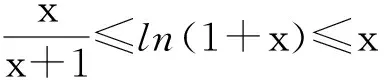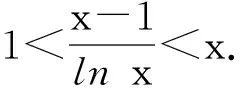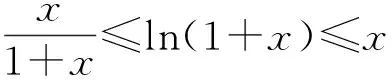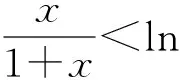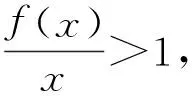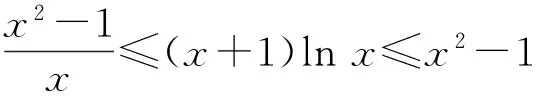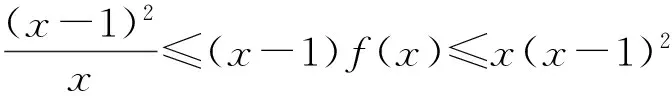全国卷高考命题中的一个热点问题*
●
(南头中学,广东 深圳 518052)
题目利用函数的单调性,证明下列不等式,并通过函数图像直观验证:ex>1+x,其中x≠0.
(人教A版《数学(选修2-2)》第32页习题1.3B组第1题第3)小题)
这个不等式的证明很容易,只需构造函数
f(x)=ex-x-1(其中x∈R),
由f′(x)=ex-1知:当x>0时,f′(x)>0;当x<0时,f′(x)<0,故当x=0时,f(x)min=f(0)=0,即当x∈R时,f(x)≥f(0),即ex-x-1≥0,亦即ex≥x+1(当且仅当x=0时,等号成立).
1 不等式ex>1+x(其中x≠0)的背景与演绎
本题的背景是泰勒展开式.泰勒公式得名于英国数学家布鲁克·泰勒,他主要以泰勒公式和泰勒级数出名,他在1712年的一封信里首次叙述了这个公式.
泰勒公式是一个用函数在某点的信息描述其附近取值的公式,是用若干项(无限或者有限)连加式(级数)来表示一个函数,这些相加的项由函数在某一点的导数求得.
对于函数f(x)=ex,它在x=0处的泰勒展开式如下:
上式也叫ex的麦克劳林展开式.当0 (3) 综合式(2)和式(3),便得 (4) 注意上述式(1)和式(2)均是在0 事实上,不等式(1)可以加强为如下两个不等式 ex≥1+x(其中x∈R),(5) (6) 式(4)可以加强为 (其中x>-1),(7) 当且仅当x=0时,式(5)~(7)中的等号成立. 不等式(5)和不等式(6)的几何解释如图1所示,不等式(7)的几何解释如图2所示[1-2]. 图1 图2 不等式ex>1+x(其中x≠0)的深刻内涵和重要作用,可以通过图3中的演绎变换中窥见一斑[3]. 图3 方法1变形. 由不等式(5),知ex-1≥x恒成立,若ex-1≥ax对于x≥0恒成立,则a≤1,于是当x≥0时,x(ex-1-ax)≥0恒成立,故a≤1. 据此,可编拟2010年全国数学高考课标卷Ⅰ文科第21题第2)小题: 例1设函数f(x)=x(ex-1)-ax2,若当x≥0时,f(x)≥0,求a的取值范围. 方法2替换、变形. 在不等式ex≥1+x中,作替换x→-x,可得 e-x≥1-x, 即 (1-x)ex≤1, 上式两边同时乘以1+x(其中x≥0),可得 (1-x2)ex≤1+x. 可见,当x≥0时,(1-x2)ex≤ax+1恒成立,则 ax+1≥x+1, 即a≥1. 据此,可编拟2017年全国数学高考卷Ⅱ文科第21题第2)小题: 例2已知函数f(x)=(1-x2)ex,当x≥0时,f(x)≤ax+1,求a的取值范围. 方法3取倒数、变形. 当x>-1时,由ex≥1+x>0,两边取倒数可得 从而 即 据此,可编拟2010年全国数学高考大纲卷Ⅱ理科第22题第1)小题: 方法4演绎、变换. 由于ex≥1+x(其中x∈R)(当且仅当x=0时,等号成立),若令x>0,作替换x→x-1得ex-1≥x,即ex≥ex,则两边取倒数,可得 (8) 当且仅当x=1时,等号成立.进一步由ex-1≥x,两边取倒数,得 (9) 上式两边取以e为底的对数,得 据此,可编拟2014年全国数学高考卷Ⅰ理科第21题: 1)求a,b; 2)证明:f(x)>1. 注1由第1)小题知a=1,b=2,从而 CMV感染是艾滋病患者最常见的疱疹病毒感染,可分为CMV血症和器官受累的CMV病。CMV可侵犯患者多个器官系统,包括眼睛、肺、消化系统、中枢神经系统等,其中CMV视网膜脉络膜炎是艾滋病患者最常见的CMV感染。 注2由本题改编的问题还有2015年全国高中数学联赛陕西省预赛题第二试第5题: 例5已知函数f(x)=xlnx,g(x)=-x2+ax-3,其中a∈R. 方法1直接引用. 不等式ln(1+x)≤x表明,函数不等式f(x)=ln(1+x)-x≤0恒成立(当且仅当x=0时,等号成立). 据此,可编拟2004年全国数学高考卷Ⅱ理科第22题第1)小题: 例6已知函数f(x)=ln(1+x)-x,求函数f(x)的最大值. 方法2赋值、累加. 一方面, 即 另一方面,当n≥3时, 综上所述,当n≥3时, 据此,可编拟2017年全国数学高考卷Ⅲ理科第21第2)小题: 方法3嵌入系数. 由式(7),可知ln(1+x)≤x(其中x>-1),于是 lnx≤x-1(其中x>0), 据此,可编拟2017年全国数学高考卷Ⅲ理科第21题第1)小题: 例8已知函数f(x)=x-1-alnx,若f(x)≥0,求a的值. 方法1替换、变形. 据此,可编拟2016年全国数学高考卷Ⅲ文科第21题第2)小题: 方法2变形、传递. 一方面,由式(1)知 ex≥1+x(其中x∈R), 由式(6)知 从而 x+1≥ln(x+2), 于是 ex≥1+x≥ln(x+2). (11) 在式(11)中,当x=0时,ex≥1+x取到等号;当x=-1时,1+x≥ln(x+2)等号成立,因此 ex>ln(x+2), 即 ex-ln(x+2)>0. 另一方面,已知当m≤2时, ln(x+2)≥ln(x+m), 故当m≤2时, ex-ln(x+m)≥ex-ln(x+2)>0. 据此,可编拟2013年全国数学高考卷Ⅱ理科第21题第2)小题: 例10已知函数f(x)=ex-ln(x+m),求证:当m≤2时,f(x)>0. 方法3变形、嵌入. 据此,可编拟2006年全国数学高考卷Ⅱ理科第20题: 例11设函数f(x)=(1+x)ln(1+x),若对所有的x≥0都有f(x)≥ax成立,求实数a的取值范围. 方法4综合、演绎. (其中x>0),(12) 当且仅当x=1时,等号成立. 在不等式(12)中,先分别乘以x+1,得 再分别加上1-x,得 (13) 令f(x)=(x+1)lnx-x+1.一方面,由不等式(13)知 当且仅当x=1时,等号成立.若x≥1,则 若0 注意到当x>0时, 从而 (x-1)f(x)≥0. 另一方面,由不等式(12)得 lnx-x≤-1, 即lnx-x的最大值为-1.若假定lnx-x-a≤0恒成立,则 a≥(lnx-x)max=-1. 由lnx-x-a≤0,得 x(lnx-x-a)≤0, 即 xlnx≤x2+ax, 从而 xlnx+1≤x2+ax+1. 注意到xlnx+1=xf′(x),因此,若xf′(x)≤x2+ax+1恒成立,则a≥-1. 据此,可编拟2010年全国数学高考卷Ⅰ理科第20题: 例12已知函数f(x)=(x+1)lnx-x+1. 1)若xf′(x)≤x2+ax+1,求a的取值范围; 2)证明:(x-1)f(x)≥0. [1] 方亚斌.用ex的幂级数展开式编演绎高考题[J].数学通讯,2012(2):50-53. [2] 方亚斌.源于世界数学名题的高考题赏析[M].杭州:浙江大学出版社,2017. [3] 方亚斌.源于课本的高考题数学题赏析[M].杭州:浙江大学出版社,2017.
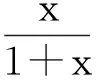
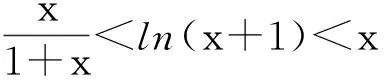
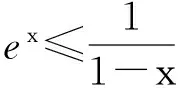

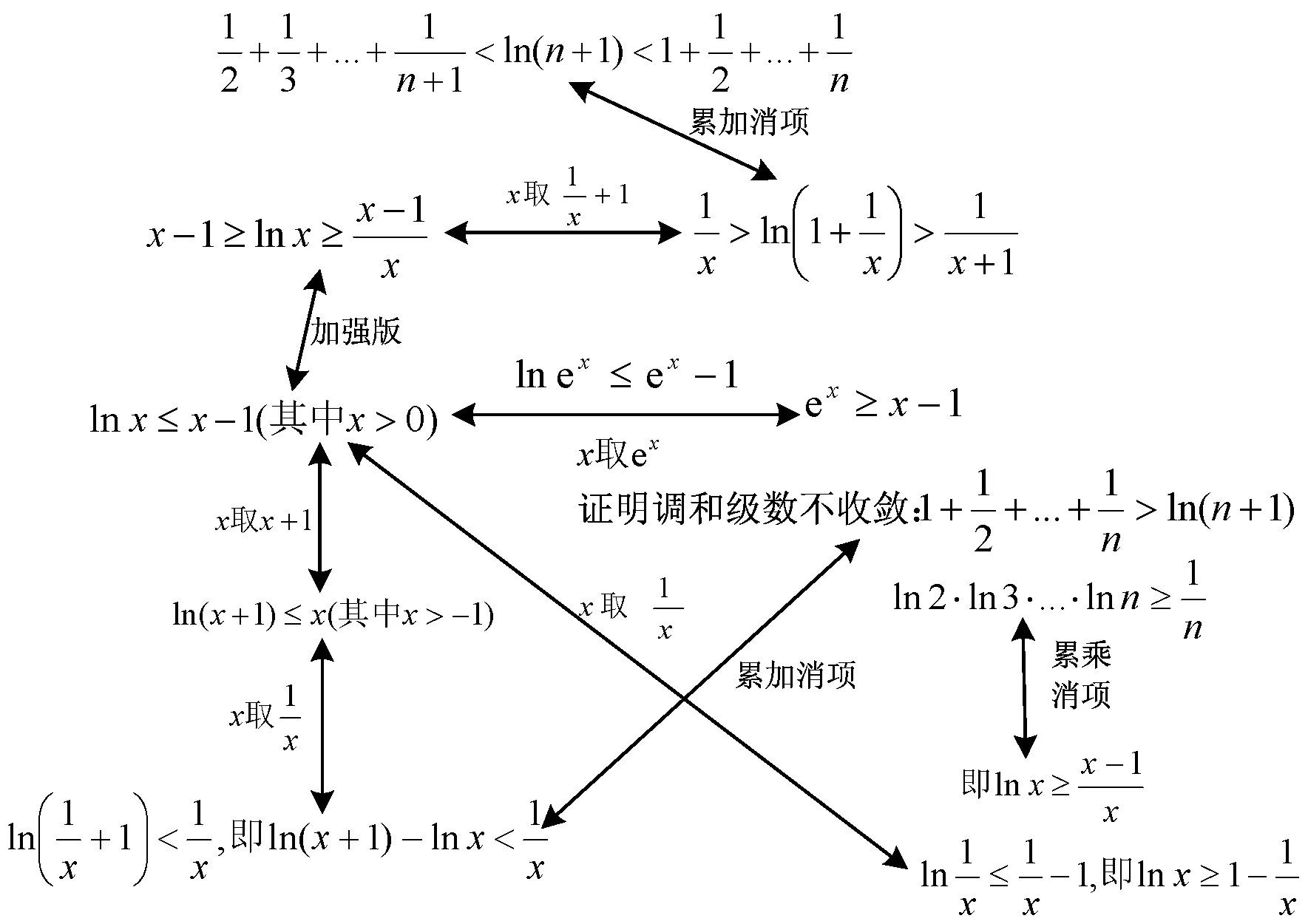
2 不等式ex≥1+x(当且仅当x=0时,等号成立)演绎高考题
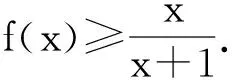

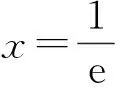

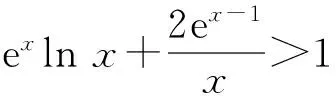
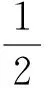
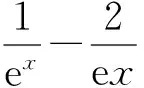
3 不等式ln(x+1)
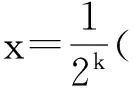

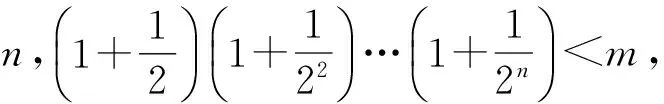
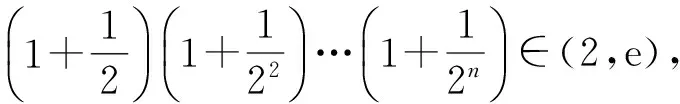
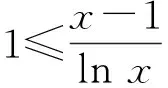

4 不等式演绎高考题