数形结合思想方法*

●

(学军中学，浙江 杭州 310000)

1 考点回顾

数形结合是中学阶段重要的思想方法，是培养学生直观想象能力的重要途径，是提升学生核心素养的重要载体.从数到形，由形到数，让学生在分析问题和解决问题中提升素养.从数到形，问题更加直观；由形到数，问题更加严谨，更加贴近数学的本质.

数形结合思想是浙江省数学高考重点考查的内容之一.浙江省试题具有简洁严谨的特点，非常注重学生对问题本身的理解，对数形结合思想的考查常从概念出发，形成图形，然后解决问题.如2017年浙江省数学高考试题第3～5,7,10,15,17,21题，都与数形结合有关，可以预测：数形结合思想仍将是2018年浙江省数学高考考查的重点和热点之一.

2 典题剖析

分析如图1，点A在以O为圆心、BC为直径的圆上，由已知条件得

图1

从而

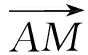
评注本题关键在于形的构造，找到点M动的原因是点A在圆上运动，由此将问题转化为对投影的分析，通过寻找两个极端位置，顺利实现对本题的突破.

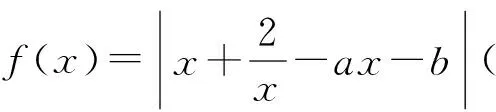
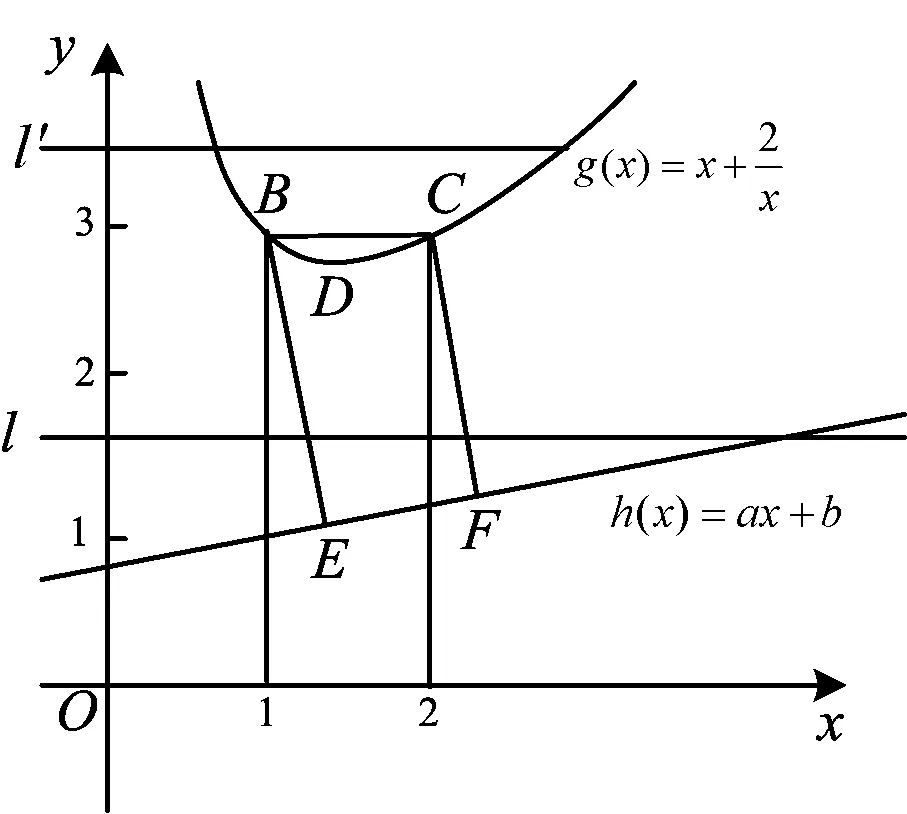
图2

评注本题关键在于对绝对值的分析，转化为两个函数纵向距离差的最大值，逐步分析，最终找到取到复合最小值的位置.

例3若不等式(ax+3)(x2-b)≤0对任意的x∈(0,+∞)恒成立，则 ( )

A.ab2=9 B.a2b=9,a<0

C.b=9a2,a<0 D.b2=9a

图3

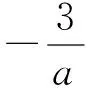
评注从两个函数的图形特点出发，分析两个函数零点必有一个重合的条件，本题通过一个图，巧妙地回避了很多讨论，非常灵巧.

A．必为正数 B．必为负数

C．必为非负 D．必为非正

图4

分析由题意知f′(x)=x2-2x+a，设A,B为f′(x)的两个零点，则

f′(t+2)>0.

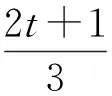
评注本题的数形结合一气呵成，从中发现点E是1～t之间的三等分点，这是本题最大的亮点，充分说明图形是解决问题的重要载体.

例5设函数f(x)=x2-ax+a+3，g(x)=ax-2a，存在x0∈R，使得f(x0)≤0与g(x0)≤0同时成立，求实数a的最小值.

分析对a进行讨论：

综上所述，a的最小值为7.

图5 图6

评注问题的关键在于对于同一个x0，函数值均不大于0，反映在图像上均小于0，这个关键在于排除a≤0的情况，然后找到a>0情形的边界条件.

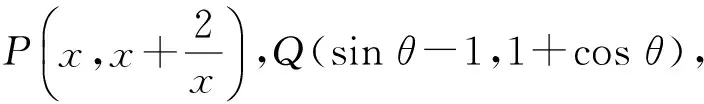
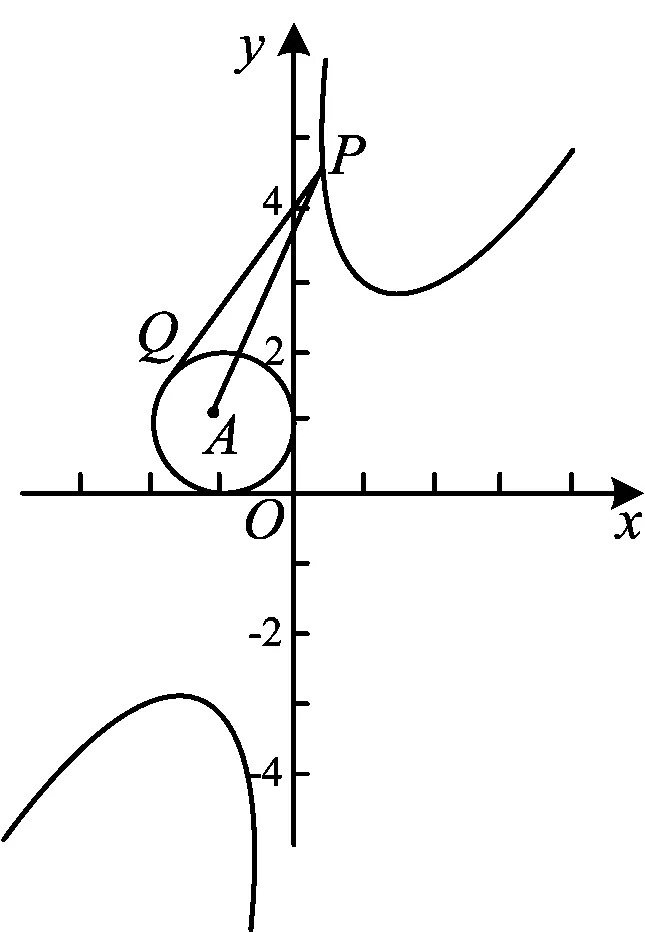
图7

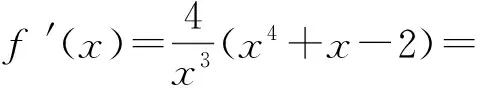
评注把代数问题转化为距离问题，把两个动点距离问题转化为圆到打勾函数的距离问题.这是本题的亮点，也是数形结合的重要运用.本题通过图形发现问题、分析问题，然后解决问题.

3 精题集萃

2.已知向量a,b满足|a|=1，|b|=2，则|a+b|+|a-b|的最大值是______，最小值是______.

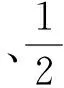
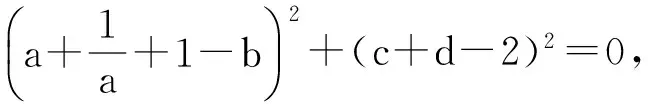
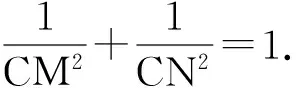
参考答案

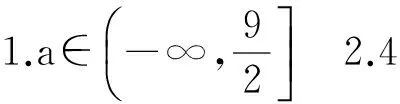
图8 图9

7.解如图9，联结AC,MN交于点F.由点N,F,M共线可知

由点A,F,C共线可知

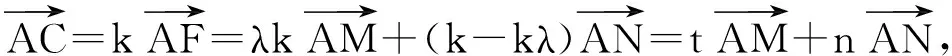
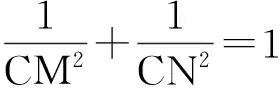
图10

[1] 范迪飞,朱哲．以“本”为据 以“思”促教——高三数学解题教学的实践与思考[J]．中学教研(数学)，2017(12)：9-12.

[2] 张春杰．数形结合思想方法[J]．中学教研(数学)，2017(2)：23-26.