数学“三势能”让思维转换更自然*
●
(萧山区第六高级中学,浙江 杭州 311261)
1 缘起
匈牙利数学家路莎·彼得所说:“数学家们解题往往不是对问题进行正面攻击,而是将它不断变形,而是把它们变为能够得到解决的问题.”我们在学习过程中,经常会碰到不同的教学思路、不同的解题方法、不同的视角去解决同一个问题.不同的视角之间的思维转换如何才能实现?怎样才能更加自然?如何提高学生思维转换的主动性?这些都是我们值得研究的课题.
2 操作与实践
势能是储存于一个系统内的能量,也可以释放或者转化为其他形式的能量.虽然这是一个物理学上的概念,但数学本身就是一个庞大、复杂的系统,因此我们可以认为数学内部具有巨大的势能,通过一定方式将其能量释放出来就能为数学的发展做出贡献.高中数学也可以充分利用此类“势能”进行思维转换,笔者根据自己的实践把它分为顺势、造势、蓄势.
2.1 思维转换之顺势转换
任何新事物产生之前,必定会有一些萌芽.解题也是如此,首先要分析条件与目标,仔细阅读题目的各个主要部分,依次对它们进行考虑.目标的内容是什么,会涉及哪些相关知识与方法;条件与目标呈现的是怎样的一种数学结构,与已经学过的知识是否存在直接的联系或类似性.这些都是题目中所蕴含的势能,我们要顺着这些势能实现思维转换.
因此所谓顺势就是通过目标指引、结构分析等手段把问题化归到学生所熟悉的知识或方法,也就是接近学生的最近发展区.据此笔者把它分为顺目标之势与顺结构之势.
1)顺目标之势.
目标原则是思维转换的基本原则之一,其作用就是指引.方向可以是条件到结论,也可以从结论到条件,本质就是已知与未知的互化.
案例1解三角形一例.

转化1将条件转化为
但与利用余弦定理求cosA有差异.
转化2不放弃,将余弦定理代入式(1)化简得
(2)
此式形式已达最简,但离目标sinA或cosA较远.
此时有学生提出由式(1)和式(2)结合余弦定理与平方关系联立可以解出b,c,sinA,cosA.想法不错,充分利用了方程的思想,但耗时耗力.
转化3此时需要另辟蹊径,回头检查并没发现问题,观察式(2)得
即

点评此题实际上是以前解三角形问题中求周长最值(或面积)问题的延伸.如已知△ABC中,a,b,c分别是内角A,B,C的对边,A=60°,a=2,求周长(或b+c)的最大值.利用余弦定理结合基本不等式可解决.

反思此题结构简单却不能直接到达目标,虽说联立方程可行却难以操作,此时题目的难点就像爬山即将到达山顶一样,只要一阵凉风吹来并想想目标所在即可顺势而下突破难点.
2)顺结构之势.
著名的布尔巴基学派的基本指导思想就是结构主义,他们认为全部数学基于3种结构:代数结构、序结构和拓扑结构.高中数学学习,特别是思维的转换自然离不开对结构的分析.无论是实际问题或情景的结构,还是抽象的数学问题的结构,要实现条件与目标的相互转换都需分析其本质结构.可按识别结构、再进行联想结构、转换结构的步骤进行.
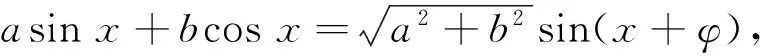
案例2函数单调性定义运用.

A.(-∞,0) B.(-∞,1)
C.(-1,0)∪(0,3) D.(-∞,0)∪(0,1)
此题乍一看无从下手,联想单调性定义就可以依据其结构进行逐步转化.
条件转化1)联想函数单调性定义:变形为

2)联想分式不等式解法:函数g(x)=f(x)+x在R上单调递增.
目标转化结构转换1:换元,令t=log2|3x-1|,则不等式可化为f(t)<2-t;
结构转换2:变形,再化为g(t) 结构转换3:求解,由条件转换2可知t<1,即log2|3x-1|<1,求得x<1. 点评单调性定义常考常变,因此有必要对定义的结构进行适当变形以加深概念的理解运用和知识模块之间的相互联系. 反思抓住数学概念的代数结构或几何结构有助于认识数学概念的本质,从而把繁难问题简单化、陌生问题熟悉化. 数学上的概念、方法是历史上经历了多年的沉积才形成的,如果直接把它放到学生面前,学生对它是陌生的,就算勉强接受也是被动的,不具有深刻性和持续性.很多数学知识高高在上,处在高位运行态势,势能强大却无法落地.我们有必要对概念的形成、定理的推导、方法的产生进行适当铺垫,营造思维转换的氛围. 因此笔者认为造势就是通过数学史融入教学、挖掘学生的最近发展区、采用多媒体或网络技术等多种方式让知识从高位势能转换为低位势能,从而实现思维的自然转换. 在教学中经常会遇到突兀性问题,如两角差的余弦公式,由三角函数线方法突然转到向量方法让人恍惚.针对这一转换可进行适当的造势以实现思维的自然转换.譬如:1)从教材的分布来讲,为什么第一章“三角函数”与第三章“三角恒等变换”之间会插入第二章“平面向量”,这不就是在诱导我们使用向量方法来解决三角问题吗?2)从已产生的公式结构来看,cosαcosβ+sinαsinβ就是x1x2+y1y2,即数量积的坐标形式.如此造势即可完成三角方法与向量方法之间的自然转换,此类问题在方法教学与解题教学中经常出现,下面再以错位相减法为例说明造势转换. 案例3错位相减法. 错位相减法是数列求和中的常用方法之一,但面对通项是等差乘等比的情形,很多学生到高三仍旧想不到此方法,这是为何? 回看教材的推导过程 Sn=a1+a1q+a1q2+…+a1qn-1,(3) 我们发现,如果用公比q乘以式(3)的两边,可得 qSn=a1q+a1q2+…+a1qn-1+a1qn,(4) 两式相减可得…… 就此我们发现“用公比q乘式(3)的两边”这一步来得太过突然,这样虽然解决了等比求和公式的推导问题,但学生思维的转换还是存在障碍的,因此有必要对思维转换进行造势.下面是笔者总结的两种造势方式. 造势1依方法造势[1]. 师:常见的求和方法有哪些? 生:倒序相加、裂项相消、错位相减等. 师:倒序相加法用来求什么数列的和? 生:等差数列. 师:能具体描述一下吗? 生:式(3)倒过来写Sn=an+an-1+…+a1.结合性质a1+an=a2+an-1=…,可得等差数列求和公式. 师:倒序相加的目的是什么? 生:减少项数得到一个简洁的公式. 师:我们再看裂项相消法,能举一个例子说明吗?怎么解答? 师:由此看出裂项的目的是什么? 生:相消即减少了项数. 师:两种求和方法的共同目的是什么? 生:减少项数. 师:能再举一个例子吗? 师:错位相减法中“用公比q乘式(3)的两边”这一步目的是什么? 生:减少项数. 由此错位相减法才真正引入了…… 造势2依目标造势. 师:类比等比数列的通项公式an=a1qn-1,前n项和Sn应该用什么量表示? 生:首项和公比. 师:通项代入后 Sn=a1+a1q+a1q2+…+a1qn-1, 怎样减少项数?等比数列中你还有什么知识可用? 生:利用等比数列定义,每一项乘公比变成后一项. 师:后面各项提出q后变成怎样一个式子? 生:Sn=a1+q(a1+aq+…+a1qn-2),即Sn-qSn=a1-a1qn-1. 师:这不就是错位相减法的框架吗?我们将其变形为错位相减法: Sn=a1+a2+…+an, qSn=a2+…+anq, 两式相减得 (1-q)Sn=a1-a1qn-1, …… 点评两种造势方式各有侧重,造势1侧重如何引入和式两边同乘公比这一方法,造势2侧重目标的构成研究. 理解数学概念、方法产生的历程,把数学知识的学术形态转化成教育形态是数学教学基本目标之一.虽然我们并不是很清楚高斯是如何得到错位相减这种求和方法的,但我们通过造势使学生的思维转换顺利实现,这就达成了教学的目标. 文献[2]中提到了10种转换机制,如:正面问题反面化、整体问题局部化、运动问题静止化等等.要让学生形成这些转换机制,日常教学中教师不仅要重视基础知识、基本技能的巩固,也要重视基本思想方法、基本数学活动经验的积累,这就是我们经常强调的四基.只有当四基的储备到达一定层次,就像水库蓄水到一定水位水流才能倾泻而出,学生的思维之花才能绽放,笔者称之为蓄势. 蓄势首要当然是双基的积累,不再赘述.这里笔者着重提出处理数学问题的方法与策略的积累. 2.3.1 蓄方法之势 数学的解题方法很多,对不同的问题有不同的方法.如求函数的值域问题:二次函数可用配方法、数形结合法;一次分式型函数可用分离常数法、反函数法;高次函数可用导数法等等.有时对同一个问题有不同视角的多种解法,如下面这个解析几何题,笔者就采用了解析法、向量法、几何法等多种方法.方法的积累我们姑且称之为蓄方法之势. 1)求直线AP斜率的取值范围; 2)求|PA|·|PQ|的最大值. (2017年浙江省数学高考试题第21题) 方法1解析法 1)设点P(x,y),易得直线AP的斜率k∈(-1,1). 2)联立直线AP与BQ的方程解出点Q,再进一步求得 |PA|·|PQ|=(1-k)(k+1)3. 令f(k)=(1-k)(k+1)3,其中k∈(-1,1),则 此法运算量超大,人称“暴力解法”,主要表现为3步:一是求点Q坐标,二是用弦长公式计算|PA|·|PQ|,三是导数法求最值.每一步的运算量都不小,虽说解决解析几何问题必须有扎实的运算功底,但作为核心素养的数学运算,首先要研究清楚算法,选择适当的算法是必要的,因此有必要换一个视角处理长度之积,即进行思维转换. 方法2向量法 向量转换2考虑到AP⊥BQ,运用向量运算或投影法可将|PA|·|PQ|进一步转换为 方法3几何法 圆幂转换由AP⊥BQ联想到圆,点Q在以AB为直径的圆上,由圆幂定理可知 以下同方法1和方法2. 点评3种方法实现了几何问题解析化再到几何法的多次转换,可见命题人立意之深.高考中解析几何题的正确解答,可以实现从中等得分到高分的跨越,此题不仅考查了解析几何知识,还必须使用导数知识才能解决最值问题,方法1将耗费学生大量时间,因此需要平时积累方法对思维进行转换,由此可见蓄势的重要性. 反思高考试题是讲究区分度的,要想在难度系数比较高的题目中拿到分数,不仅要掌握高中数学的四基,也要掌握常见的思维转换方式,如代数与几何的互化、高维问题低维化、一般问题特殊化等等.在经历一定程度的训练后才能实现熟能生巧,因此三势中蓄势才是最重要的. 2.3.2 蓄策略之势 以上我们提到蓄方法之势,对解题方法的使用其实还只是程序性知识.对一些重要的知识模块中的常见问题或常见题型,必须对其进行适当拓展和提升,使其上升为能够让学生接受的策略性知识,称之为蓄策略之势.下面以数列前n项和的最值问题为例加以说明. 案例5等差数列的前n项和的最值问题. 已知等差数列{an},a1=26,a2=22,则其前n项和Sn何时取得最大值? 本题可采用单调性法和二次函数法解决(略).对于一般的等差数列{an},我们均可以采用以上两种方法加以解决,再升级后还可成为其他数列求最值的方法. 方法1(符号法)由首项及通项的符号确定Sn的最值. 方法2(函数法)利用Sn是n的函数,利用函数知识求最值. 求解最值. 点评从一个题目的解决,推广到一类问题的解决,再上升到策略性知识,这让学生的思维不仅深刻而且广阔. 反思学生不仅要会解一个题目,而且要能够推广到一般情形.在推广过程中也会发现,并不是每种方法都适用任何情形或题目,因此在解题过程中我们会选择适当的策略,以把控解题的方向避免无谓的损失.策略的选择需要日常的学习经验的积累,即蓄策略之势. 通过近几年的实践,我们发现数学“三势能”对学生的思维转换的主动性、灵活性、缜密性等起到了非常重要的作用[3].顺势、造势实现了势能从高位到低位的转换,而蓄势实现了低位到高位的转换.总之,数学三势能有助于实现思维的自然转换,对数学学习的效率提升大有作用,值得大家去进一步研究. [1] 李湘.顺应学生思维 促进学生发展[J].中学数学月刊,2017(5):21-24. [2] 李发武,李良贵.引入转换机制解题[J].数学通报,2001(4):26-28. [3] 周晓.高中数学教学要培养学生转换思维的能力[J].考试周刊,2015(79):73-74.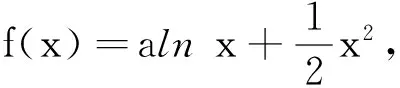
2.2 思维转换之造势转换

2.3 思维转换之蓄势转换



3 结束语
——《势能》

