基于路P8m+4t+2的交错标号的图S(4m+1,4(t+1),4m-1)的优美标号*
吴跃生
(华东交通大学理学院,江西 南昌330013)
基于路P8m+4t+2的交错标号的图S(4m+1,4(t+1),4m-1)的优美标号*
吴跃生
(华东交通大学理学院,江西 南昌330013)
给出了图S(4m+1,4(t+1),4m-1)的定义;讨论了图S(4m+1,4(t+1),4m-1)的优美性,证明了图S(4m+1,4(t+1),4m-1)是优美图;给出了由路P8m+4t+2的交错标号构造图S(4m+1,4(t+1),4m-1)的优美标号的四种算法。
优美图;交错图;优美标号;交错标号;路;圈

图的优美标号问题是组合数学中一个热门课题[1-17]。1988年,Rosa给出了三角仙人掌,四角仙人掌,五角仙人掌等概念;1989年Mouton对三角仙人掌的特殊情形三角蛇的优美性给出了证明[2]。
1 若干概念
定义1[2]所有的块皆为Cm的连通图,称为m角仙人掌(或称Cm仙人掌)。
定义2[2]在顶点最大度为4的m角仙人掌中,如果每个Cm至多有二个度为4的点,且度为4的点构成一条简单通路,则称此m角仙人掌为Cm蛇。
定义3 块分别为Cm,Cn,Cq的连通图,称为(m,n,q)角仙人掌。
定义4 在顶点最大度为4的(m,n,q)角仙人掌中,如果Cm,Cn,Cq至多有二个度为4的点,且度为4的点构成一条简单通路,则称此(m,n,q)角仙人掌为(m,n,q)蛇。记为S(m,n,q)。
本文讨论了图S(4m+1,4(t+1),4m-1)的优美性。
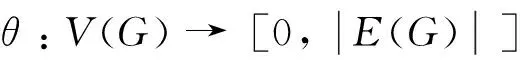
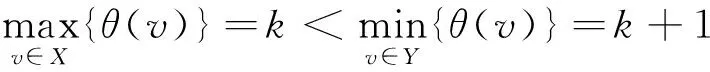
2 主要结果及其证明
定理1 对任意自然数m,t(m≥1),图S(4m+1,4(t+1),4m-1)存在缺标号值 5m+2t+1,5m+2t+2和6m+3t+3的优美标号。
证明 设V(C4m+1)={u0,u1,u2,…,u4m},
定义图S(4m+1,4(t+1),4m-1)的标号θ为
下面证明θ是图S(4m+1,4(t+1),4m-1)的优美标号。
1)θ:{u2i+1:i=0,1,2,…,4m+2t}→
[4m+2t+1,8m+4t+4]-
{5m+2t+1,5m+2t+2,6m+3t+3}
是双射;
是双射;所以
θ:V(S(4m+1,4(t+1),4m-1))→
[0,8m+4t+2]-{5m+2t+1,5m+
2t+2,6m+3t+3}
是双射;
2)
θ′(u2i+1u2i+2)=
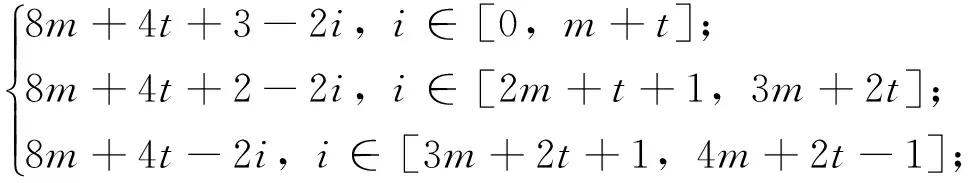
θ′(u2i+1u2i)=
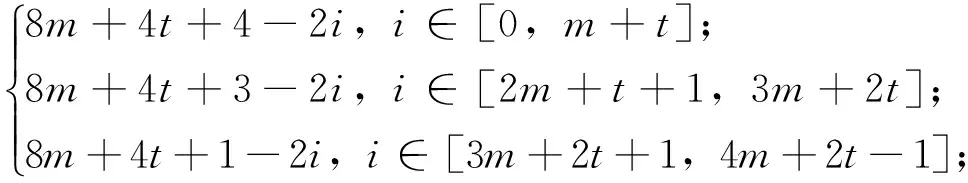
θ′:E(C4(t+1))→[4m+1,4m+4t+4}是双射;
θ′(u8m+4t+1u4m+4t+3)=2m+1;
θ′:E(C4m-1)→[1,2m-1]∪[2m+1,4m]是双射;
θ′:E(S(4m+1,4(t+1),4m-1))→[1, 8m+4t+4]是一一对应
由1)和2)可知θ就是图S(4m+1,4(t+1),4m-1)缺标号值5m+2t+1,5m+2t+2和6m+3t+3的优美标号。证毕。
由定理1可给出图S(4m+1,4(t+1),4m-1)的优美标号的第一种算法:
第一步:先给出路P8m+4t+2的交错标号θ如下:设
第二步:将路P8m+4t+2的交错标号值不小于6m+3t+1的均加3,将路P8m+4t+2的交错标号值不小于5m+2t+1不大于6m+3t的均加2,其余的交错标号值不变;
第三步:在路P8m+4t+2中的顶点u0和u4m之间加连一条边(在标号值为0,2m的两个顶点之间加连一条边),在路P8m+4t+2中的顶点u4m和u4m+4t+3之间加连一条边(在标号值为2m,6m+2t+2,的两个顶点之间加连一条边),路P8m+4t+2中的顶点u4m+4t+3和u8m+4t+1之间加连一条边(在标号值为4m+2t+1,6m+2t+2的两个顶点之间加连一条边)。
例1 当m=2,t=1时,由定理1图S(9,8,7)的优美标号的第一种算法如下:
第一步:先给出路P22的交错标号如图1所示;
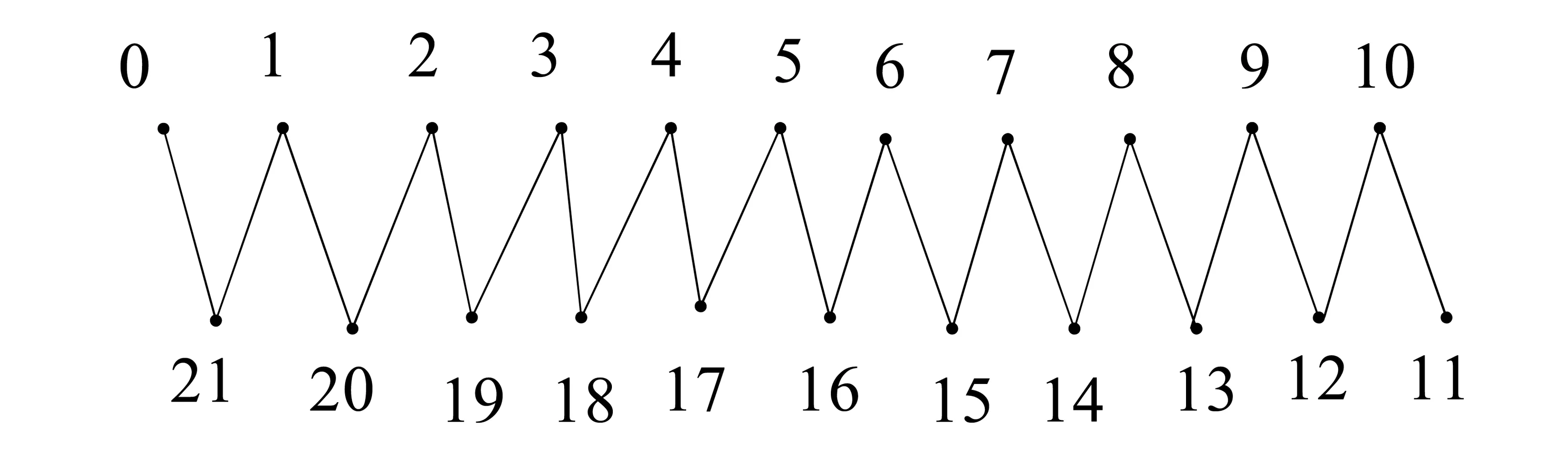
图1 路P22的交错标号Fig.1 The alternating graceful labeling of P22
第二步:将路P22的交错标号值不小于16的均加3,将路P22的交错标号值不小于13不大于15的均加2,其余的交错标号值不变;
第三步:在路P22中的顶点u0和u8之间加连一条边(在标号值为0,4的两个顶点之间加连一条边) 在路P22中的顶点u8和u15之间加连一条边(在标号值为4,16的两个顶点之间加连一条边),在路P22中的顶点u15和u21之间加连一条边(在标号值为11,16两个顶点之间加连一条边)。
由此得到图S(9,8,7)缺标号值13,14和18的优美标号,图S(9,8,7)缺标号值13,14和18的优美标号如图2所示。

图2 图S(9,8,7)的第一种优美标号Fig.2 The first graceful labeling of S(9,8,7)
定理2 对任意自然数m,t(m≥2),图S(4m+1,4(t+1),4m-1)存在缺标号值 3m+2t+2,3m+2t+3和6m+3t+3的优美标号。
证明 设V(C4m+1)={u0,u1,u2,…,u4m},
E(C4m+1)={u0u1,u1u2,…,u4m-1u4m,u4mu0},
V(C4(t+1))={u4m,u4m+1,…,u4m+4t+3},
E(C4(t+1))={u4mu4m+1,u4m+u4m+2,…,
u4m+4t+2u4m+4t+3,u4m+4t+3u4m},
V(C4m-1)={u4m+4t+3,u4m+4t+4,…,u8m+4t+1},
E(C4m-1)={u4m+4t+3u4m+4t+4,u4m+4t+4u4m+4t+5,…,
u8m+4tu8m+4t+1,u8m+4t+1u4m+4t+3},
定义图S(4m+1,4(t+1),4m-1)的标号θ为:

由定理2可给出图S(4m+1,4(t+1),4m-1)的优美标号的第二种算法:
第一步:先给出路P8m+4t+2的如图1所示的交错标号。
第二步:将路P8m+4t+2的交错标号值不小于6m+3t+1的均加3,将路P8m+4t+2的交错标号值不小于3m+2t+2不大于6m+3t的均加2,其余的交错标号值不变;
第三步:在路P8m+4t+2中的顶点u0和u4m之间加连一条边(在标号值为0,2m的两个顶点之间加连一条边),在路P8m+4t+2中的顶点u4m和u4m+4t+3之间加连一条边(在标号值为2m,6m+2t+2,的两个顶点之间加连一条边),路P8m+4t+2中的顶点u4m+4t+3和u8m+4t+1之间加连一条边(在标号值为4m+2t+3,6m+2t+2的两个顶点之间加连一条边)。
例2 当m=2,t=1时,由定理2图S(9,8,7)的优美标号的第二种算法如下:
第一步:先给出路P22的交错标号如图1所示;
第二步:将路P22的交错标号值不小于16的均加3,将路P22的交错标号值不小于10不大于15的均加2,其余的交错标号值不变;
第三步:在路P22中的顶点u0和u8之间加连一条边(在标号值为0,4的两个顶点之间加连一条边) 在路P22中的顶点u8和u15之间加连一条边(在标号值为4,16的两个顶点之间加连一条边),在路P22中的顶点u15和u21之间加连一条边(在标号值为13,16两个顶点之间加连一条边)。
由此得到图S(9,8,7)缺标号值10,11和18的优美标号,图S(9,8,7)缺标号值10,11和18的优美标号如图3所示。
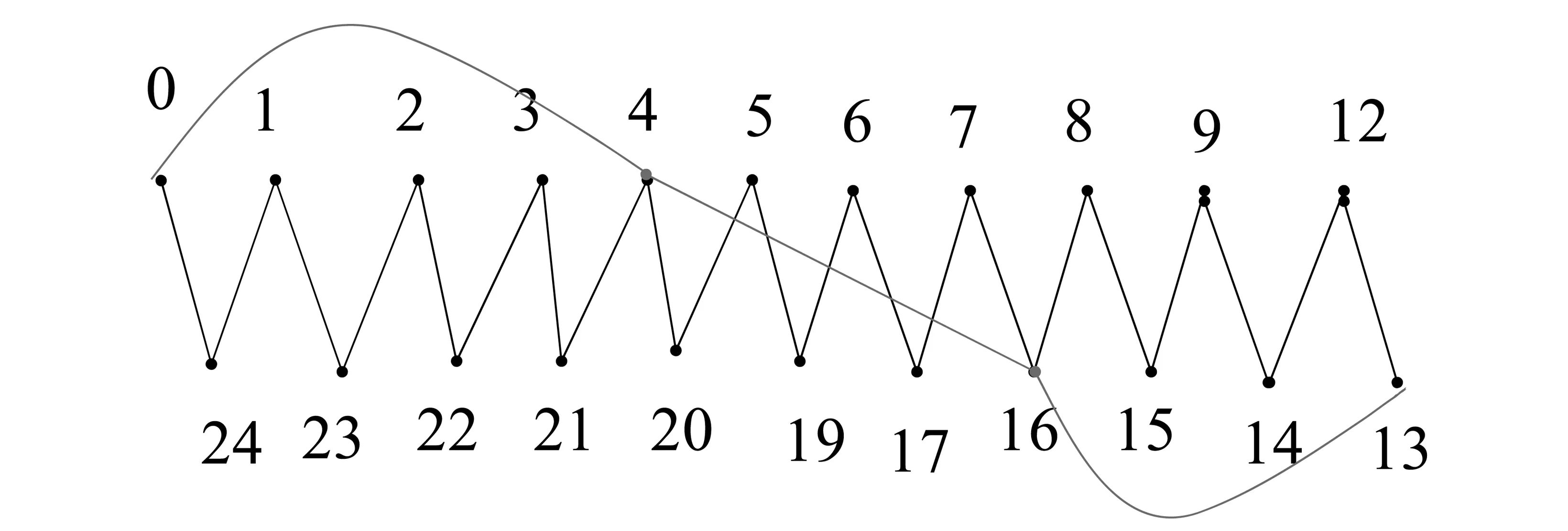
图3 图S(9,8,7)的第二种优美标号Fig.3 The second graceful labeling of S(9,8,7)
定理3 对任意自然数m,t(m≥2),图S(4m+1,4(t+1),4m-1)存在缺标号值 3m+2t+3,3m+2t+4和2m+t+1的优美标号。
证明 设V(C4m+1)={u0,u1,u2,…,u4m},
E(C4m+1)={u0u1,u1u2,…,u4m-1u4m,u4mu0},
V(C4(t+1))={u4m,u4m+1,…,u4m+4t+3},
E(C4(t+1))={u4mu4m+1,u4m+u4m+2,…,
u4m+4t+2u4m+4t+3,u4m+4t+3u4m},
V(C4m-1)={u4m+4t+3,u4m+4t+4,…,u8m+4t+1},
E(C4m-1)={u4m+4t+3u4m+4t+4,u4m+4t+4u4m+4t+5,…,
u8m+4tu8m+4t+1,u8m+4t+1u4m+4t+3},
定义图S(4m+1,4(t+1),4m-1)的标号θ为:
仿定理1,可以验证θ是图S(4m+1,4(t+1),4m-1)的缺标号值 3m+2t+2,3m+2t+3和6m+3t+3的优美标号。证毕。
由定理3可给出图S(4m+1,4(t+1),4m-1)的优美标号的第三种算法:
第一步:先给出路P8m+4t+2的如图1所示的交错标号。
第二步:将路P8m+4t+2的交错标号值不小于3m+2t+2的均加3,将路P8m+4t+2的交错标号值不小于2m+t+1不大于3m+2t+1的均加1,其余的交错标号值不变;
第三步:在路P8m+4t+2中的顶点u0和u4m之间加连一条边(在标号值为0,2m的两个顶点之间加连一条边),在路P8m+4t+2中的顶点u4m和u4m+4t+3之间加连一条边(在标号值为2m,6m+2t+3,的两个顶点之间加连一条边),路P8m+4t+2中的顶点u4m+4t+3和u8m+4t+1之间加连一条边(在标号值为4m+2t+4,6m+2t+3的两个顶点之间加连一条边)。
例3 当m=2,t=1时,由定理2图S(9,8,7)的优美标号的第二种算法如下:
第一步:先给出路P22的交错标号如图1所示;
第二步:将路P22的交错标号值不小于10的均加3,将路P22的交错标号值不小于6不大于9的均加1,其余的交错标号值不变;
第三步:在路P22中的顶点u0和u8之间加连一条边(在标号值为0,4的两个顶点之间加连一条边) 在路P22中的顶点u8和u15之间加连一条边(在标号值为4,17的两个顶点之间加连一条边),在路P22中的顶点u15和u21之间加连一条边(在标号值为14,17两个顶点之间加连一条边)。
由此得到图S(9,8,7)缺标号值11,12和6的优美标号,图S(9,8,7)缺标号值11,12和6的优美标号如图4所示。
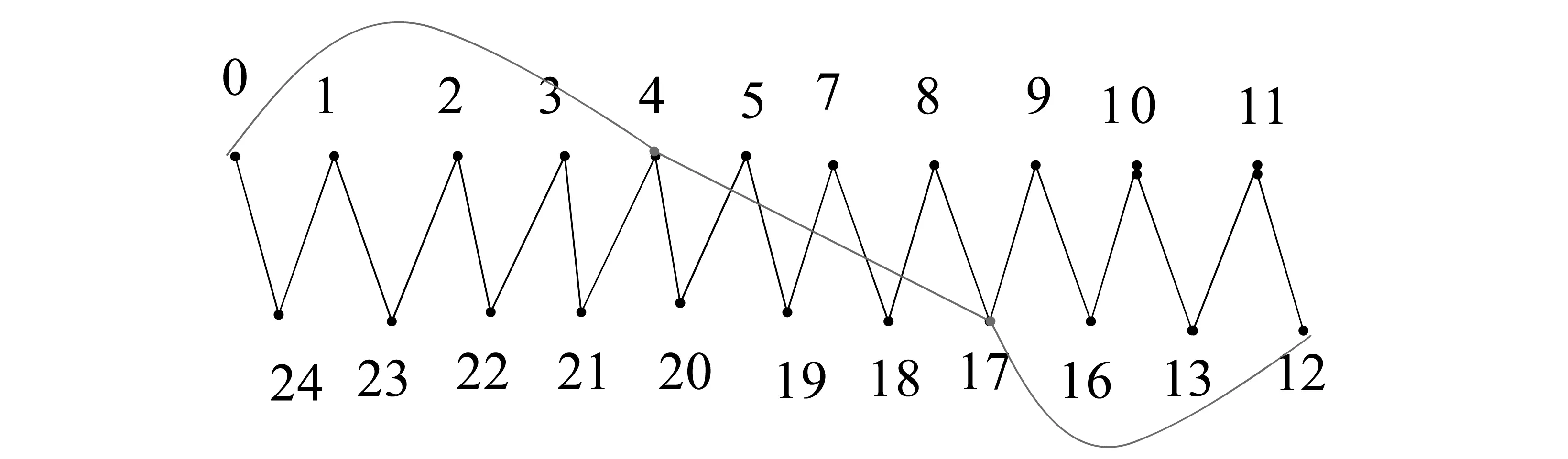
图4 图S(9,8,7)的第三种优美标号Fig.4 The third graceful labeling of S(9,8,7)
定理4 对任意自然数m,t(m≥2),图S(4m+1,4(t+1),4m-1)存在缺标号值 5m+2t+2,5m+2t+3和2m+t+1的优美标号。
证明 设V(C4m+1)={u0,u1,u2,…,u4m},
E(C4m+1)={u0u1,u1u2,…,u4m-1u4m,u4mu0},
V(C4(t+1))={u4m,u4m+1,…,u4m+4t+3},
E(C4(t+1))={u4mu4m+1,u4m+u4m+2,…,
u4m+4t+2u4m+4t+3,u4m+4t+3u4m}
V(C4m-1)={u4m+4t+3,u4m+4t+4,…,u8m+4t+1},
E(C4m-1)={u4m+4t+3u4m+4t+4,u4m+4t+4u4m+4t+5,…,
u8m+4tu8m+4t+1,u8m+4t+1u4m+4t+3},
定义图S(4m+1,4(t+1),4m-1)的标号θ为:
仿定理1,可以验证θ是图S(4m+1,4(t+1),4m-1)的缺标号值 5m+2t+2,5m+2t+3和2m+t+1的优美标号。证毕。
由定理4可给出图S(4m+1,4(t+1),4m-1)的优美标号的第四种算法:
第一步:先给出路P8m+4t+2的如图1所示的交错标号;
第二步:将路P8m+4t+2的交错标号值不小于5m+2t+1的均加3,将路P8m+4t+2的交错标号值不小于2m+t+1不大于5m+2t的均加1,其余的交错标号值不变;
第三步:在路P8m+4t+2中的顶点u0和u4m之间加连一条边(在标号值为0,2m的两个顶点之间加连一条边),在路P8m+4t+2中的顶点u4m和u4m+4t+3之间加连一条边(在标号值为2m,6m+2t+3,的两个顶点之间加连一条边),路P8m+4t+2中的顶点u4m+4t+3和u8m+4t+1之间加连一条边(在标号值为4m+2t+2,6m+2t+3的两个顶点之间加连一条边)。

图5 图S(9,8,7)的第四种优美标号Fig.5 The fourth graceful labeling of S(9,8,7)
例4 当m=2,t=1时,由定理2图S(9,8,7)的优美标号的第二种算法如下:
第一步:先给出路P22的交错标号如图1所示;
第二步:将路P22的交错标号值不小于13的均加3,将路P22的交错标号值不小于6不大于12的均加1,其余的交错标号值不变;
第三步:在路P22中的顶点u0和u8之间加连一条边(在标号值为0,4的两个顶点之间加连一条边) 在路P22中的顶点u8和u15之间加连一条边(在标号值为4,17的两个顶点之间加连一条边),在路P22中的顶点u15和u21之间加连一条边(在标号值为12,17两个顶点之间加连一条边)。
由此得到图S(9,8,7)缺标号值14,15和6的优美标号,图S(9,8,7)缺标号值14,15和6的优美标号如图5所示。
[1] 马克杰. 优美图[M]. 北京:北京大学出版社,1991: 1-247.
[2] 何梅. 图2Cn的优美性[J]. 内蒙古大学学报:自然科学版,1995, 26(3): 247-251.
[3] 杨显文. 关于C4m蛇的优美性[J]. 工程数学学报,1995, 12(4): 108-112.
[4] 吴跃生, 李咏秋. 关于圈C4h+3的(r1, r2,…,r4h+3)-冠的优美性[J]. 吉首大学学报:自然科学版,2011, 32(6): 1-4.
[6] 吴跃生. 图C7(r1,r2,r3, ,r4,r5,0,0)∪St(m )的优美性[J]. 吉首大学学报:自然科学版, 2012, 33(5): 9-11,25.
[7] 吴跃生. 关于圈C4h+3的(Gr1, Gr2,…,Gr4h+3)-冠的优美性[J]. 吉首大学学报:自然科学版,2013, 34(4): 4-9.
[8] GALLIAN J A. A dynamic survey of graph labeling [J]. The Electronic Joumal of Combinatorics, 2013,19, DS6:1-306.
[9] 吴跃生. 连通图G+e∪Hk-1的优美性[J]. 吉首大学学报:自然科学版,2014, 34(2): 3-5.
[10] 吴跃生,王广富,徐保根. 非连通图C2n+1(r1,r2, …,rn+1)∪Gm的优美性[J]. 西南大学学报:自然科学版,2014, 36(8): 83-86.
[11] 吴跃生.非连通图C4m-1∪G的优美性[J]. 吉首大学学报:自然科学版,2014, 34(3): 1-3.
[12] ABRHAM J,KOTZIG A. All 2-regular graphs consisting of 4-cycles are graceful [J]. Discrete Mathematics, 1994 ,135(1/2/3): 1-14.
[13] 吴跃生,王广富,徐保根.关于图G1∪G2⊙K1的优美性[J]. 江西师范大学学报:自然科学版,2014, 38(3): 236-239.
[14] 贾慧羡,左大伟. 与扇图相关的2类图的超边优美标号[J]. 吉首大学学报:自然科学版,2014, 35(2): 6-9.
[15] 杨思华,姚兵,张婉佳. 一致仙人掌树的Felicitous性质[J]. 湖南师范大学:自然科学学报,2014, 37(3): 87-90.
[16] 吴跃生. 再探非连通图C4m-1∪G的优美标号[J]. 吉首大学学报:自然科学版,2015, 36(1): 1-4.
[17] 吴跃生. 非连通图C3(m,0,0)∪G的优美性[J]. 华东交通大学学报, 2013, 30(6): 35-39.
The Graceful Labeling of the GraphS(4m+1,4(t+1),4m-1) Based on the Balanced Labeling of the PathP8m+4t+2
WUYuesheng
(School of Science, East China Jiaotong University, Nanchang 330013, China)
A definition of the graphS(4m+1,4(t+1),4m-1) is given. The gracefulness of the graphS(4m+1,4(t+1),4m-1) is discussed. It is proved that ifm≥1,t≥0, the graphS(4m+1,4(t+1),4m-1) is a graceful graph.Based on the alternating labeling ofP8m+4t+2, four algorithms of the graceful labeling ofS(4m+1,4(t+1),4m-1) are given.
graceful graph; alternating graph ; graceful labeling; alternating labeling; path; cycle
10.13471/j.cnki.acta.snus.2015.05.005
2015-01-20
国家自然科学基金资助项目(11261019,11361024);江西省教育厅2014年度科学技术研究资助项目(GJJ14380)
吴跃生(1959年生),男;研究方向:图论;E-mail:616100567@qq.com
O157.5
A
0529-6579(2015)05-0019-05

