几种叉积图的平衡指标集

陈碧英

（武夷学院 数学与计算机学院，福建 武夷山 354300）

1 预备知识

定义 1.1[2]设 f:V（G）→ ｛0，1｝是图 G 的一个顶点标号映射,则由f可诱导出图G的一个部分边的标号 f*:E（G ）→｛0，1｝，对任意的 uν∈ E（G）,当且仅当f（u）=f（ν）时，有 f*（uν）=f（u）；若 f（u）≠ f（ν），则边 uν未被 f* 标号.称 Bf（G）=ef（1）-ef（0）为图 G 的平衡标号。

定义 1.2[2]称图G的这个标号 f为友好标号；称 BI （G为友好标号｝为图G的平衡指标集。

定义 1.3[3]设 f:V（G）→ ｛0，1｝是图 G 的一个点标号映射，定义 g:V（G）→｛-0.5,0.5｝，其中 g=f-0.5.则由g诱导出相应的边标号映射g*:E （G）→ ｛-1,0，1｝，g*（uν）=g（u）+g（ν）,∀ uν∈ E（G ）。

命题1.1[3]若记 νg（i)为在点标号 g下V（G）中标号为i的顶点数，eg（i)为在g导出的边标号g*下E （G ）中标号为 i的边数，Bg（G）=eg（1）-eg（-1）。因此g*（e）=-1 等价于 f*（e）=0，g*（e）=1 等价于 f*（e）=1，g*（e）=0等价于在 f中 e不标号。

命题 1.2[3]f为友好标号等价于≤1,g为友好标号。

命题1.3[3]对于图G的一个｛-0.5，0.5｝标号，记

引理 1.1[3]若 g为 G=｛V（G）,E（G）｝的任意一个｛-0.5,0.5｝标号，则有

定义 1.4 称一个图是（r,s）-正则的（r≠ s），如果这个图的每个点的度数都是r或者s。

命题 1.4[3]若 G=｛V（G）,E（G）｝为（r,s）-正则图，g为 G 的任意一个｛-0.5，0.5｝标号，则：

定理1.1[3]若g为r-正则G的任意一个｛-0.5，0.5｝标号，则 Bg（G ）（其中分别表示度为r的点中标号为0.5和-0.5的点的数目。）

定义 1.5 称一个图是（r,s,t）-正则的 （r≠s≠ t），如果这个图的每个点的度数都是r或者s，或者t。

命题 1.5 若 G＝（V,E）为 （r,s,t）-正则图，g 为 G的任意一个｛-0.5，0.5｝标号，则：

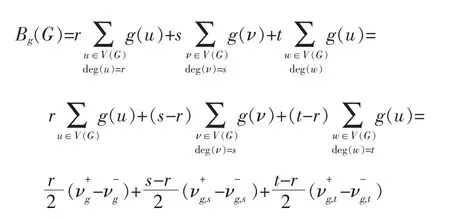
定义1.5 称一个图是 （r,s,t,y）-正则的 （r≠s≠t≠y），如果这个图的每个点的度数都是r或者s，或者t，或者 y。

命题 1.6 若 G＝（V,E）为（r,s,t,y）-正则图，g 为 G的任意一个｛-0.5，0.5｝标号，则

设 G1＝（V1,E1）与 G2＝（V2,E2）是两个图,G1与 G2的叉积图定义为：G1×G2=（V,E），其中

且（ν1，ν2）∈E2｝

注意到任意图G的平衡指标集为非负整数集合。为了书写的方便，对于非负整数a，b且a＜b，通常用［a，b］来表示［a，b］的所有整数，即若 BI（G ）=［a，b］，则BI（G）=｛a，a+1，…,b-1,b｝。

Km,n为完全二部图，Cn为n个顶点的圈，Pn为 n个顶点的路，Wn为n个顶点的轮图。在参考文献[4-5]中给出 Cm×Cn和 P2×Pn的平衡指标集。

2 若干叉积图的平衡指标集

定理 2.1 BI（Wm×Wm）=

证明：(1)m=2 时 W2×W2是 4-正则图。

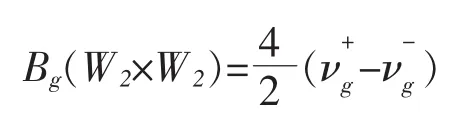
W2×W2共有9个点，设g为友好标号，则Bg（W2×W2）∈ ｛±2｝故 BI（W2×W2）=｛2｝。

(2)m=3 时，W3×W3是 9-正则图。

W3×W3共有6个点，设g为友好标号，则

Bg（W3×W3）＝0.故 BI（W3×W3）=｛0｝。

(3)m≥ 4 时，Wm×Wm是（9,3m,m2）-正则图，其中9度点有m2个，3m度点有2m个，m2度点有1个。

设 r=9,s=3m,t=m2，则

Wm×Wm共有（m+1）2个点，由于 m≥ 4 时，m2≥ 2m+1。取遍每一个值，Wm×Wm都存在友好标号。

当（m+1）2为偶数时，即m为奇数时，设g为友好标号，则

引理2.1 设A≥2为一正整数，则

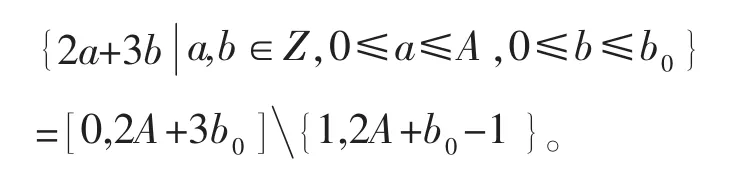
证明：用数学归纳法来证.

（1）当 A=2 时，2a=0,2,4,则 2a+3b 可以取 0,2,4（b=0）;3,5,7（b=1）;6,8,10（b=2）;9,11,13（b=3）;12,14,16（b=4）… 3b0-6,3b0-4,3b0-2（b=b0-2）;3b0-3,3b0-1,3b0+1（b=b0-1）;3b0,3b0+2,3b0+4（b=b0）。

因 此，2a+3b取遍 了 0,2,3,4,5,6… ,3b0-3,3b0-2,3b0-1,3b0,3b0+1,3b0+2,3b0+4.故此时结论成立。

（2）假设结论对A≤k-1成立，下证结论对A=k也成立。

当 a＜k 时，2a+3b 可以取 0,2,3,… ,2（k-1）+3b0-2,2（k-1）+3b0。

当a=k时，2a+3b可以取2k,2k+3,2k+6,…,2k+3(b0-1),2k+3b0。

故2a+3b所有可能的取值为0,2,3,…,2k+3b0-3,2k+3b0-2,2k+3b0所以命题成立。

定理 2.4 BI（K2,m×K1,m）=证明：（1）m=1 时，P3×P2是（1,2）正则图，其中 1

度点有4个，2度点有2个。设r=1，s=2则故 Bg（P3×P2）∈ ［-1，1］。故 BI（P3×P2）=｛0,1｝。

(2)m=2 时，K2,2×K1,2是（2,4）-正则图，其中 2 度点有8个，4度点有4个。

设r=2,s=4则

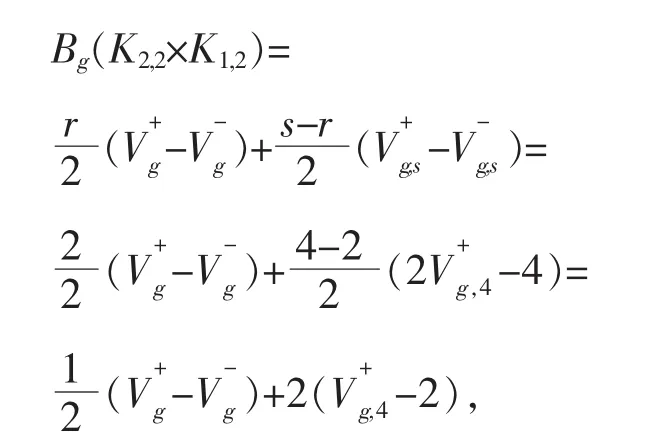
其中：V+g,4∈ ［0，4］。

故 Bg（K2,2×K1,2）∈ ｛0，±2，±4｝。故 BI（K2,2×K1,2）=｛0，2，4｝。

(3)m=3 时，K2,3×K1,3是（2,3,9）- 正则图，其中 2 度点有12个，3度点有6个，9度点有2个。

设 r=2,s=3,t=9，则

故 Bg（K2,3×K1,3）∈ ［-10,10］。故 BI（K2,3×K1,3）=[0,10]。

(4）m≥ 4 时，K2,m×K1,m是 （2,m,2m,m2）正则图，其中2度点有m2个，m度点有2m个，2m度点有m个，m2度点有2个。

故 Bg（K2,3×K2,3）∈ ［-18,18］{±17}。

故 BI（K2,3×K2,3）∈ ［0,18］{17}。

(4）m=4 时，K2,4×K2,4是 （4,8,16）-正则图，其中 4度点有16个，8度点有16个，16度点有4个。

设 r=4,s=8,t=16，则

一个值时，K2,m×K2,m都存在友好标号。

当m2+4m+4为偶数时，即m为偶数时，设g为友好标号，则

故 Bg（K2,m×K2,m）∈{0，±（2m-4）,±2（2m-4）,… ,±（3m+2）（2m-4）}。

故 BI（K2,m×K2,m）∈ {0，2m-4,2（2m-4）,…,（3m+2）（2m-4）}。

当m2+4m+4为奇数时，即m为奇数时，设g为友好标号，则

故 Bg（K2,m×K2,m）∈ {±2,±（m-2）±2,±2（m-2）±2,… ,±（6m+4）（m-2）±2}。

3 结论

通过证明得到 Wn×Wn，Cm×Cn，K1,m×K1,m，K2,m×K1,m，K2,m×K2,m叉积图的平衡指标集的准确值。