平面体系存在无穷远虚铰时几何组成分析

范卫琴，颜玲月，张红章

（1.三明学院 建筑工程学院，福建 三明 365004；2.武汉市丰达地质工程有限公司，湖北，武汉 430074）

结构几何组成分析目的主要是：判定杆件体系是否几何可变，从而决定其能否用作结构；研究结构的几何组成，同时有助于结构静力分析。很多学者对几何组成分析规则进行了一系列总结和梳理，得出较为详尽的分析方法[1-4]。但这些文献对平面体系中存在无穷远虚铰时的分析方法论述较少，且举例偏简单，总结不完整，教材中也没有对此进行专门的论述。针对这个难点，文献[5-7]根据射影几何的相关概念推导出平面体系存在无穷远铰情况下的判定法则，还有学者[8]在结构自由度为零的情况下，运用“零载法”进行计算，认为当体系内力为零是唯一解时，体系几何不变；当体系内力有无穷多非零解时，体系几何瞬变。

通常几何组成分析的方法主要有“铰接三角形规律”、“零载法”等[9]。很明显，对于一个自由度为零的体系，在零载下，当结构内力有无穷多非零解时，结构体系有可能是几何瞬变、也有可能是几何常变，与论著[8]不一致。当结构存在着成对平行链杆时，根据近代欧式几何学[10]认为此对平行链杆在无穷远处相交于一点，即形成一个无穷远虚铰，再依据相关文献[5-7]论述的规则来进行平面体系几何组成分析，有些情况下会得出不同的结果，现通过分析某三刚片体系的内部几何组成性质予以证明。

1 举例分析

1.1 解法一

如图1所示，平面体系由一系列链杆连接而成，图中 AF、BC、FE、CD 四杆等长。选取杆件 AB、FC、ED分别为刚片Ⅰ、Ⅱ、Ⅲ，Ⅰ和Ⅱ之间通过AF和BC这对平行且等长链杆相连、Ⅱ和Ⅲ之间通过FE和CD这对平行且等长链杆相连，分别形成无穷远虚铰，即“二铰无穷远”。Ⅰ和Ⅲ之间通过杆件AD和BE相连，相交于G点。根据法则[5-7]“当结构有两个无穷远虚铰时，组成两个无穷远虚铰的两对平行链杆相互平行且等长，则常变。”据此，图1结构应为几何常变体系。

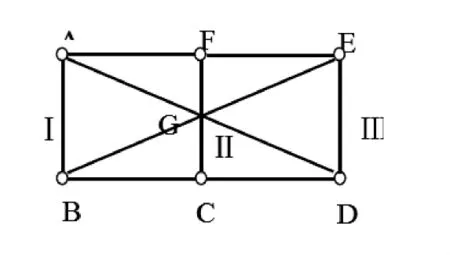
图1 示例及第一种选取刚片的方法Figure 1 Example and the firstmethod for selecting a rigid piece

1.2 解法二

对图1的杆件体系，选择不同对象为刚片和连接链杆，见图2。选取杆件AD、FC、BE分别为刚片Ⅰ、Ⅱ、Ⅲ，Ⅰ和Ⅱ之间通过杆件AF和CD这对平行且等长链杆相连、Ⅱ和Ⅲ之间通过杆件FE和BC这对平行且等长链杆相连、Ⅰ和Ⅲ之间通过杆件AB和ED这对平行且等长链杆相连，分别形成无穷远虚铰，即“三铰无穷远”。根据法则[5-7]“三铰无穷远，若三对平行链杆各自等长，则常变。”据此，图1所示结构应为几何常变体系。

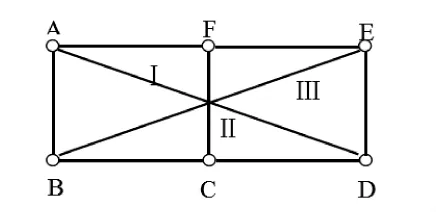
图2 第二种选取刚片的方法Figure 2 Second method for selecting rigid plates

1.3 解法三

针对图1的杆件体系，再次改变刚片的选择方式，选取杆件AF、BE、CD分别为刚片Ⅰ、Ⅱ、Ⅲ，见图3。Ⅰ和Ⅱ之间通过杆件AB和FE相交于虚铰A，Ⅱ和Ⅲ之间通过杆件ED和BC相交于虚铰D，Ⅰ和Ⅲ之间通过杆件FC和AD相连，铰点为G，此次分析，三个铰点未出现无穷远的情况，A、D、G三点在一条直线上，根据“三刚片”法则[9]，图1所示结构应为几何瞬变体系。

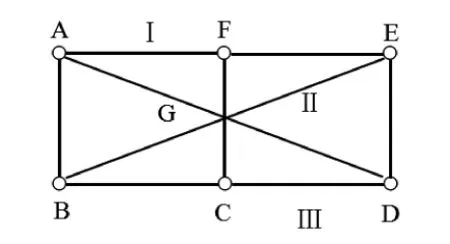
图3 第三种选取刚片的方法Figure 3 Thirdmethod for selecting rigid plates

由此可见，解法一、二的结果与解法三不一致。第三种分析方法中没有出现无穷远铰点，根据“三刚片法则”[9]得出的结果可靠，由此判定：前两种方法不够准确。

2 问题探讨

近代欧式几何学[10]中有如下定义：（1）两条或多条平行线可以说成有一公共的无穷远点，或者在无穷远处相交；（2）在任一条直线上，有且只有一个无穷远点；（3）所有的无穷远点都在一条无穷远直线上。

由此很多学者都指出：平行链杆相当于无穷远处的虚铰，然而，在欧式平面上平行线是无交点的。因此，采用无穷远交点来判断几何组成分析，给出的答案不够精准。

祁皑[11]指出：（1）当三刚片体系中有一铰无穷远时，当另外两个铰的连线与组成无穷远铰点的两条平行链杆不平行时，几何不变；当体系发生微小位移后，另外两个铰的连线与组成无穷远铰点的两条平行链杆仍然平行时，几何常变；反之当体系发生微小位移后，另外两个铰的连线与组成无穷远铰点的两条平行链杆不平行时，几何瞬变。

（2）当三刚片体系中有两铰无穷远时，当组成无穷远铰点的两对平行链杆方向不平行时，几何不变；当组成无穷远铰点的两对平行链杆方向平行，但当体系发生微小位移后，组成无穷远铰点的两对平行链杆仍然平行时，几何常变；反之体系发生微小位移后，组成无穷远铰点的两对平行链杆不平行时，几何瞬变。

用此方法对图1结构进行几何组成分析，假定杆件AF、BC、FE、CD发生如图4所示的微小位移且保持平行状态（虚线表示假定的变形形状），则变位之后的AD1、BE1长度明显不等，而与原来相等的状态不符，则图4所示的变位是不可能的，则本例属于“两铰无穷远，发生微小位移为以后，组成无穷远铰点的两对平行链杆不可能平行”的状态，则体系瞬变。同理也可得出当选本文的“解法二”时，三铰无穷远，当发生微小位移后，组成无穷远铰的平行链杆不再保持平行状态，所以体系瞬变。采用这种判定法则，采用前述“解法一、二、三”这三种不同的刚片选取方法能得出相同的结果。

图4 假定的微小位移示意图Figure 4 Prototype of the assumed small displacement

3 规则总结

论著[11]所示的方法，相对于文献[5-7]，描述更准确。但此法需要对可能发生的各种微小变形情况从几何角度进行分析，对初学者来讲，比较繁琐。本文根据几何变形的特点在文献[5-7]结论的基础上，对平面体系存在无穷远铰点时的解题规则进行重新整理，规则中，对于前述正确的论述，本文不再解释，对于本文提出的新观点，举例证明。

3.1 平面体系存在一铰无穷远

（1）组成无穷远铰的两条平行链杆与另外两铰连线不平行时，三点不共线，几何不变。

（2）组成无穷远铰的两条平行链杆与另外两铰连线平行但不等长时，体系瞬变。

（3）组成无穷远铰的两条平行链杆与另外两铰连线同侧、平行且等长时，体系常变。如图5所示（虚线表示变形后的位置），杆件ACF与BCE中间的三根链杆AB、CD、EF平行且相等均从同侧伸出，所以结构很容易左右晃动形成平行四边形体系。

图5 平行链杆同侧连出Figure 5 Parallel link rod with parallel side out

（4）上述第（3）条中，如果两平行链杆与另外两铰连线平行且等长，但三者异侧，则体系瞬变。如图6（a）或（b），FAC、FE、BE 分别为刚片Ⅰ、Ⅱ、Ⅲ。图中实线表示原结构体系，虚线表示可能发生的微小位移。Ⅰ和Ⅱ之间通过铰点A相连，Ⅱ和Ⅲ之间通过铰点E相连，Ⅰ与Ⅲ之间通过平行链杆AD、BC相连，平行且等长的三根杆件AD、EF、BC分别从刚片Ⅲ异侧连出，则体系发生微小运动之后，无法保持BC、AD、EF三杆继续平行，如图虚线所示，体系瞬变。

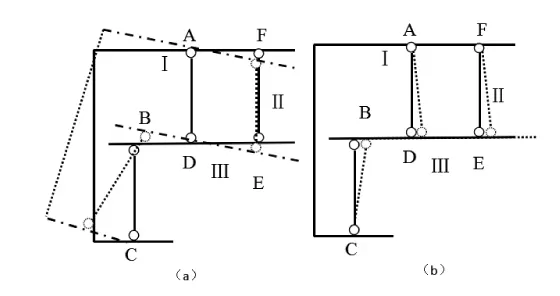
图6 平行链杆从刚片异侧连出Figure 6 Parallel chain rods connected from the lateral side of rigid plates

3.2 平面体系存在两铰无穷远

（1）组成无穷远铰的两对平行链杆相互不平行，则三铰不共点，体系几何不变；

（2）组成无穷远铰的两对平行链杆相互平行但不等长则瞬变；

（3）若上述四杆平行且等长，但从平行杆件是从刚片异侧连出时，则体系瞬变。举例见图1的示例，连接Ⅰ和Ⅱ的杆件AF和BC与连接Ⅱ和Ⅲ的杆件FE和CD分别从FC异侧伸出，体系瞬变。

（4）若上述四杆平行且等长，但平行杆件从同侧连出时，则体系常变。如图7所示，选取杆件AH、GF、BCDE分别为刚片Ⅰ、Ⅱ、Ⅲ，Ⅰ与Ⅲ之间通过AB、CK相连，形成一无穷远虚铰，Ⅱ与Ⅲ之间通过GD、FE相连，形成一无穷远虚铰，Ⅰ与Ⅱ之间连接点为H，则形成两虚铰的四根平行链杆相互平行等长，且均从刚片Ⅲ同侧连出，体系很明显可以变成平行四边形，为一几何常变体系。

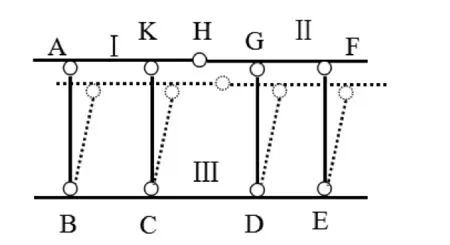
图7 平行链杆从刚片同侧连出Figure7 Parallelchain rodsconnected from thesamesideofthe rigid sheet

3.3 三铰无穷远

（1）若三对同侧平行链杆各自等长，则常变。

（2）若三对异侧平行链杆各自等长，则瞬变。举例如图2所示，在上述解法二的描述中，连接Ⅰ和Ⅱ的杆件AF和CD，分别从FC杆异侧伸出、连接Ⅱ和Ⅲ的杆件FE和BC，分别从FC杆异侧伸出、杆件AB和ED分别从Ⅰ和Ⅲ异侧伸出，属于“三对异侧平行链杆各自等长”的类型，则体系为瞬变体系。

（3）若三对平行链杆各自不等长，则体系瞬变。

4 结论

通过举例分析，对平面体系存在无穷远铰的几何组成分析的部分方法[5-7]进行了重新探讨，对“铰接三角形规律”进行了完善。建议解题时选择合适的链杆作为刚片，尽量少或避免出现无穷远虚铰。对于平面体系无法避免出现无穷远虚铰的情况，分析了这种体系微小变形后的几何特征，总结出此时几何组成分析可以遵循下列原则：

（1）当一铰无穷远时，且组成无穷远虚铰的两平行链杆与另二铰连线不平行，体系为几何不变；若二者平行不等长则为瞬变体系；若平行链杆与另二铰连线异侧、平行且等长，则为瞬变体系；若平行链杆与另二铰连线同侧、平行且等长，则为常变体系。

（2）当两铰无穷远，且组成两无穷远虚铰的两对平行链杆互不平行，体系为几何不变；若此四杆相互平行但不等长则为瞬变体系；若此四杆平行且等长但异侧连出，则为瞬变体系；若四杆同侧连出、平行且等长，则为常变体系。

（3）当三铰无穷远，一般情况下，体系瞬变；若三对同侧平行链杆各自等长，则常变；若三对平行链杆各自等长，且其中有异侧连出的平行链杆，则为瞬变体系。