GA-PSO混合算法的工作臂铰点优化设计

张小珍

（厦门大学嘉庚学院，福建 漳州 363105）

1 引言

挖掘机工作臂作为一种快速、高效施工作业机械是工程机械中的一个主要机种，受到各行业的青睐［1］。挖掘机工作臂应用对农用质量可靠性、提高农业工程效率和降低人力劳动强度等起到至关重要作用［2］。实际作业中，工作臂主要由三个油缸复合运动以及铲斗和土石方相互左右实现运动，农业工程中常出现因承载过大，造成动臂或油缸支架及工作装置铰点销轴开裂失效等问题［3］。因此，针对挖掘机工作臂铰点位置优化设计是十分有必要。通过仿真和实验相结合研究挖掘机寿命，得裂纹区域的关键点寿命，验证建立挖掘机虚拟样机模型准确性［4］。挖掘机轨迹中提出一种改进遗传算法（IGA）来搜索挖掘机最优比例、积分、微分（PID）控制器参数［5］。挖掘机工作臂运动轨迹跟踪研究中由负载不确定性和速度波动，使系统工作不稳定。

为提高跟踪性能，提出一种交叉耦合预补偿算法，与非线性比例积分控制器相结合来优化控制执行器参数［6］。为解决工作臂铰点开裂等问题，以挖掘机工作臂铰点为研究对象，对于工作装置斗杆、动臂、铲斗等部件进行参数化分析，建立运动学方程。以动臂为研究对象，对铰点位置进行优化，建立优化数学模型，借用GA-PSO混合算法提高动臂铰点位置优化，通过ADAMS软件模拟优化前后工作臂运动情况，得到各铰点受力分析，实现优化后铰点受力减小。同时，动臂优化有利于提高斗杆的挖掘力、工作效率及优化工作臂运动轨迹。

2 挖掘机工作臂分析

2.1 工作臂结构

挖掘机工作臂主要由铲斗、铲斗油缸、斗杆油缸、动臂、动臂油缸和斗杆组成［7］，如图1所示。

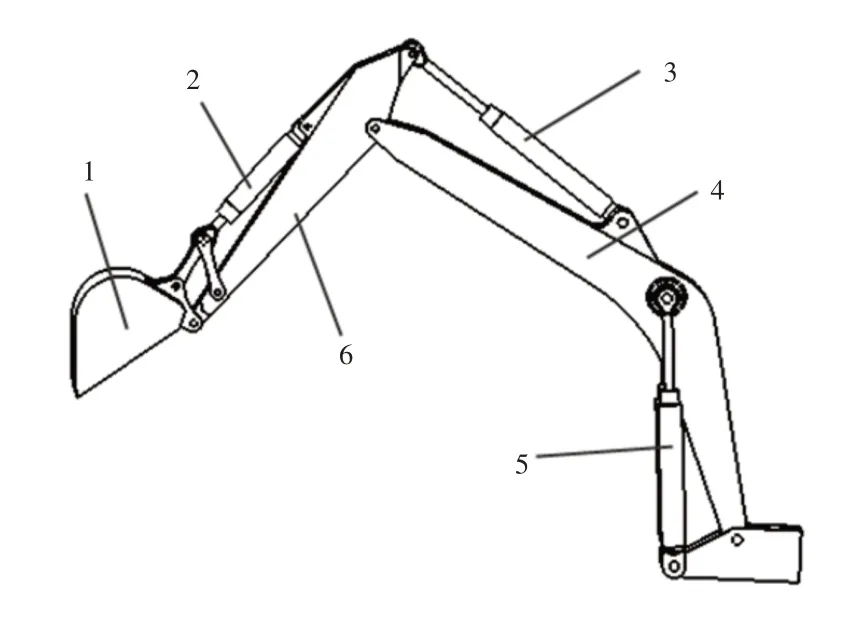
图1 挖掘机工作臂结构Fig.1 Working Arm Structure of Hydraulic Excavator

工作臂的铲斗、斗杆、动臂和三个液压油缸构成四连杆机构，实现工作臂正铲、起重、反铲等工作［8］。

铲斗是直接与货物接触，需满足不同工作环境，结构强度、刚度性能较高［9］。

斗杆由斗杆油缸驱动，实现工作臂较大工作范围［10］。动臂设计直接关系到工作承载情况和工作范围，受力较大，要求刚度较大。工作臂在工作的过程中，油缸参数，如表1所示。

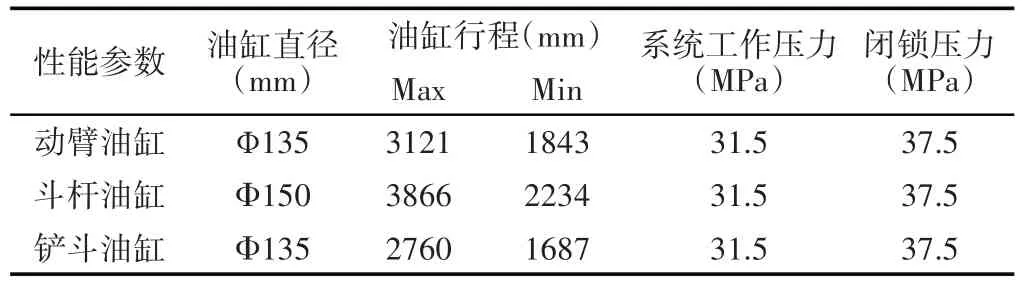
表1 各油缸的性能参数Tab.1 Performance Parmeters of Each Cylinder

2.2 动臂动力学模型建立

工作臂在工作过程由三个油缸控制工作臂运动，受到负载变化、冲击等对设计要求较高［11］。

而动臂是承载工作臂主要部件，常常会受到铲斗负载变化出现裂纹，需对动臂铰点位置参数进行设计，提高动臂提升力。建立动臂结构示意图，如图2所示。分析动臂铰点位置及受力，建立动力学模型。

图2 动臂受力分析图Fig.2 The Force Analysis Diagram of Moving Arm

铰点B、C、D、F在坐标系（ox2y2z2）中的齐次坐标：

铰点B、C、D、F的受力：

力系对质心的力矩：

动臂的动力学方程为：

3 工作臂的分析

根据工作臂三维模型，在adams软件中建立工作臂参数化模型，建立动臂模型，如图3（a）所示。动臂油缸驱动函数为step（time，0，0，6，80）+step（time，6，80，20，-80）+step（time，20，-80，40，-130），斗杆油缸step（time，0，0，10，100）+step（time，10，100，20，-300），通过动臂油缸和斗杆油缸控制着动臂整个工作，动臂向下运动，带动铲斗下降，驱动铲斗油缸，动臂油缸伸长驱动，斗杆压缩驱动，最后借助铲斗油缸压缩驱动，完成整个周期。在整个周期运动过程中发现动臂各铰点位置受力跟运动有关，如图3（b）所示。铰点A、B、C位于动臂起杆，动臂油缸在6s前向上延伸，铰点A、B、C受到动臂油缸向上推力、重物和自身重力影响，6s前受力随着时间逐渐增大，6s到40s时动臂油缸向下压缩，动臂油缸承载部分力，铰点A、B、C受力下降。对比图3（c）发现铰点A、B、C受力大于铰点D、E、F受力，其中，A铰点受力最大，E铰点受力最小。

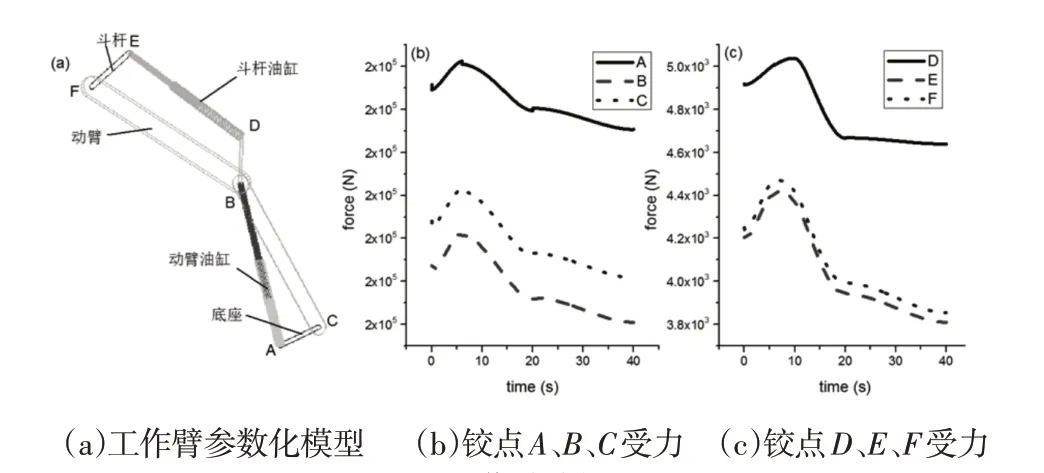
图3 工作臂分析图Fig.3 Work Arm Analysis Chart

动臂铰点受力因运动时间不同而不同，当铰点坐标位置发生变化时，铰点受力是否发生变化。

研究B铰点x、y、z坐标改变后各铰点受力情况，如图4所示。（a）铰点A受力，（b）铰点B受力，（c）铰点C受力，（d）铰点D受力，（e）铰点E受力，（f）铰点F受力，下文表示相同。

图4 改变铰点B的x坐标铰点受力分析Fig.4 The Force of Point After Changing x Coordinate of Hinge Point B

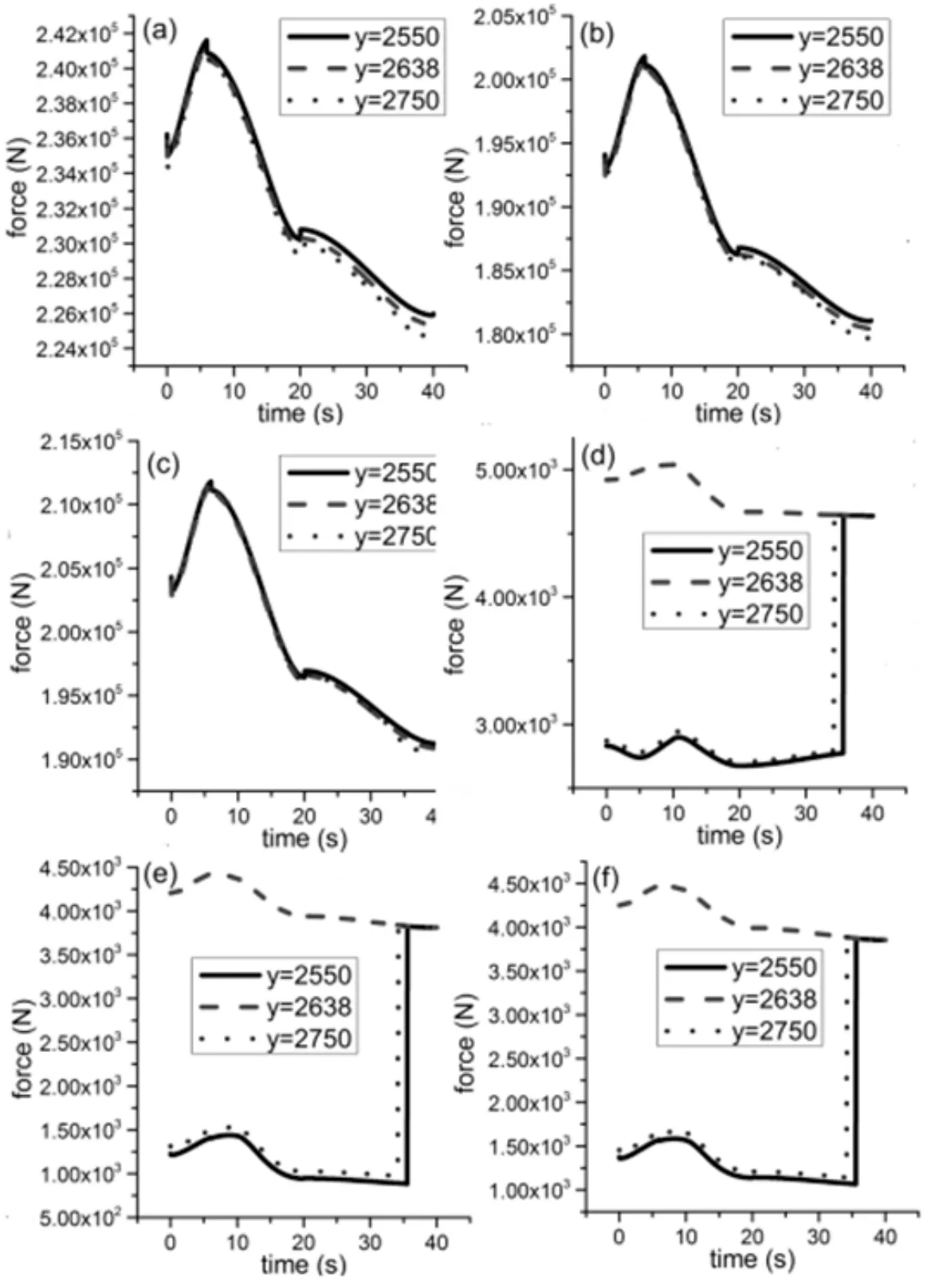
图5 改变铰点B的y坐标铰点受力分析Fig.5 The Force of Point After Changing y Coordinate of Hinge Point B

x=200在接近40s时D、E、F铰点受力突然增大，铰点B的x坐标位置对各铰点受力有着很大影响，需对x坐标位置进行优化，使得各铰点受力更加合理。

通过对铰点B的y坐标修改，研究各铰点受力分析，如图4所示。可知在铰点A、B、C中y=2550、2638和2750受力大小差不多，即铰点B的y坐标对受力影响数值较小。

改变铰点B在z坐标位置，如图6所示。铰点D、E、F曲线可知铰点B的z坐标位置改变给铰点D、E、F受力带来很大影响，受力存在波动。

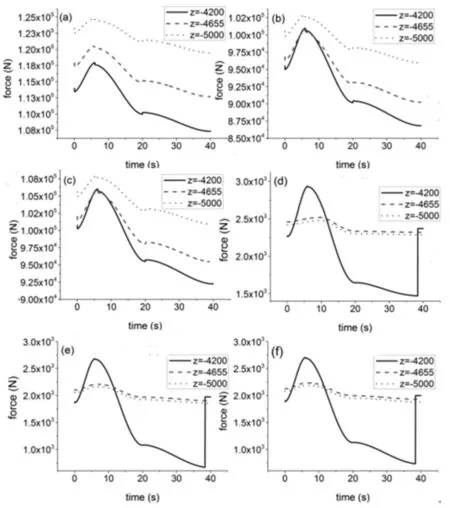
图6 改变铰点B的z坐标铰点受力情况Fig.6 The Force of Point After Changing z Coordinate of Hinge Point B

因此，提出动臂各铰点坐标位置进行调整，优化各铰点的受力，避免铰点位置因受力过大而破裂。

4 动臂优化设计

4.1 根据力学模型建立目标函数

建立动臂回转示意图，如图7所示。建立直接坐标系，画出由位置ACBDF到ACB’D’F’位置，其中标记动臂油缸下铰点为A(xA，yA，zA)，上铰点为B(xB，yB，zB)。当动臂回转时，设回转后动臂油缸上铰点为B′(xB′，yB′，zB′)，该点位置是以原CB为半径，绕C点旋转圆弧形成点。

图7 动臂回转示意图Fig.7 Rotation Diagram of Moving Arm

式中：LCB—CB的长度；α22—CB与CF的角度；β22—回转的角度。

可知，旋转后的动臂油缸的长度LAB′：

优化目标为动臂上铰点A、B、C、D、E、F受力：

4.2 确定约束条件

尽量使动臂油缸做功小，即动臂油缸行程最小LABmin延伸至最长LABmax时，动臂油缸所做功W1最小为：

其中，LABmin≤LAB≤LABmax，即1843mm ≤LAB≤3121mm

4.3 确定设计变量

动臂目标函数和约束条件都取决于动臂机构的几何变量，即各铰接点的位置，即A(xA，yA，zA)、B(xB，yB，zB)、C(xC，yC，zC)、D(xD，yD，zD)和F(xF，yF，zF)。

4.4 GA-PSO混合算法

传统遗传算法在计算过程中先进性适应度计算，然后在进行选择、变异和交叉操作，形成新种群［12］。但计算中优秀个体不能很好被保护。粒子群算法实时记忆功能，加快计算收敛能力，借GA-PSO混合算法提高工作臂优化设计参数精确度。

（1）GA算法

GA算法，即遗传算法，具体流程如下：

式中：r—随机数，取值为［0，1］。

②变异。种群中个体进行变异操作，有利于种群的多样性，实现种群中生成更加优秀的个体，操作方式为：

式中：T—最大迭代次数；Amin、Amax—个体的最小值和最大值；a—可调参数；t—迭代的次数。

（2）PSO算法

PSO算法为粒子群算法，是近些年研究的一种新方法［13］。在求解过程中，通过对比个体极值Pi和种群极值G，做出是否要更新粒子的位置和速度，更新方程为：

5 工作臂优化后对比分析

工作臂铰点位置参数优化，得动臂铰点位置优化前后坐标参数，如表2所示。

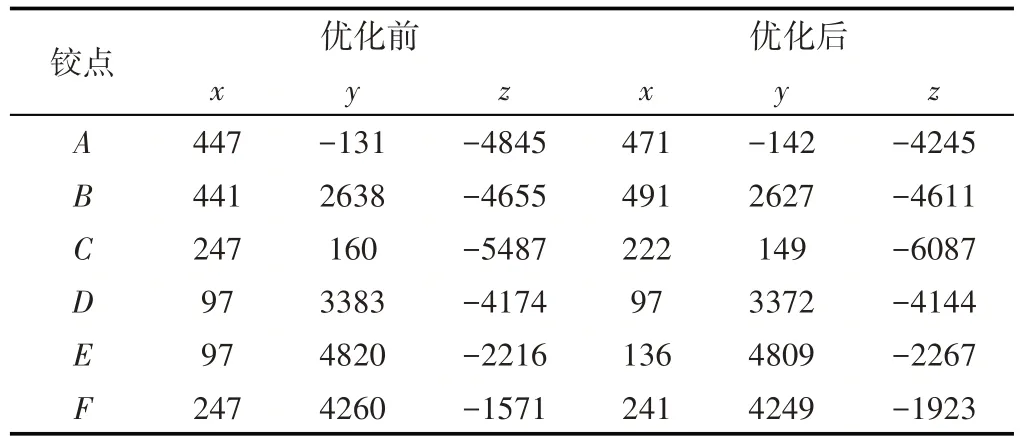
表2 铰点优化前后坐标值Tab.2 Coordinate Values Before and After Optimization of Points

优化后各铰点的受力分析，如图8所示。

图8 铰点优化前后受力情况Fig.8 Reinforcement Before and After Optimization of the Hinge Point

可知优化后各铰点的受力低于优化前，铰点A、B、C受力大于铰点D、E、F受力。

其中，铰点A受力最大，优化前为2.4×105N，优化后1.0×105N，受力降低了58%。且铰点A、B、C、E、F在整个周期运行受力波动较小，各铰点施加较均衡受力。

6 结论

挖掘机工作臂工作过程中，受到铲斗物料影响，工作臂各铰接点销轴很容易破裂，甚至断裂，影响工作臂的工作效率。

为了降低铰点受力，通过建立工作臂的三维模型，阐述各部件名称及部位，由三个部件和三个油缸构成平面四连杆机构，建立动臂动力学模型，研究动臂各铰点受到力和力矩与位置关系；确定工作臂优化函数，分析优化目标函数、约束条件和变量设计，得到优化原理；借助GA-PSO混合算法优化设计铰点坐标参数，并通过ADAMS软件仿真工作臂整个周期运动情况，得到各铰点受力分析，对比优化前后受力曲线，实现优化后铰点受力比优化前小。为连杆结构及相关结构铰点坐标参数优化提供理论研究基础。