重型多轮车辆半主动悬挂复合控制策略

田恩彤，管继富，高俊峰，曹 立

（1.北京理工大学机械与车辆学院，北京 100081；2.内蒙古第一机械集团公司，内蒙古 包头 014032）

1 引言

悬挂系统对于重型车辆来说至关重要，车辆的高机动性、高通过性和良好的乘坐舒适性都需要优良的悬挂系统来保证。随着现代车辆对于机动性和舒适性要求的提高，对悬挂性能动态的匹配也提出了要求，因此半主动悬挂和主动悬挂的应用研究十分重要。可调叶片式减振器也正是在这种要求下产生的，通过将原型减振器和流量控制阀并联，能够起到调节减振器阻尼的作用，使悬挂阻尼参数处于最佳。

当前，对于以叶片式减振器为核心的半主动悬挂已经有了很多研究。文献［1］进行了可控阻尼的叶片式减振器设计，并通过道路模拟实验台检验了可控阻尼的叶片式减振器的可控性和阻尼力调节范围，获取了阻尼系数与比例阀的输入电流I和工作液温度T之间的关系［1］。文献［2］提出了一种半主动悬挂的模糊控制算法，并分别对车体加速度和悬挂动挠度作为模糊输入进行了分析。文献［3］建立了整车多体动力学模型，通过履带车道路模拟试验台多次试验从而验证该模型的正确性。文献［4］针对磁流变半主动悬挂设计了兼顾天地棚控制有点的混合控制策略；文献［5］采用T-S模糊控制器提高了车辆的平顺性，文献［6］综合考虑行驶平顺性和操纵稳定性提出了一种最优控制算法，并在理论和实验上进行验证，文献［7］将线性二次最优控制应用在半主动控制策略开发，并与SH 控制进行对比，利用实车台架试验验证算法的有效性。文献［8］将基于屏障函数的无模型滑模控制应用在主动悬挂中并取得了良好的控制效果。

根据可调叶片式减振器的试验数据，提出了一种半主动悬挂的复合控制策略，该策略分为三层结构，上层为基于半车模型的带约束的最优控制，其主要性能指标被设置为车身俯仰角和质心垂向加速度，中间层为每个负重轮处的单轮半主动悬挂模糊控制，可以相对更加具有针对性地对每个负重轮处的半主动悬挂系统进行控制，底层为一数据驱动的可调叶片式减振器的逆模型，其主要结构为一深度置信网络，可通过上层控制器所需要的阻尼控制力反求控制电流。控制策略通过Python和Matlab/Simulink进行了联合仿真。

2 模型建立

2.1 可调阻尼叶片式减振器

可调阻尼叶片式减振器由原型叶片式减振器和比例阀系构成，根据参考文献［1］，可调阻尼叶片式减振器的简化模型和流体模型，如图1、图2所示。

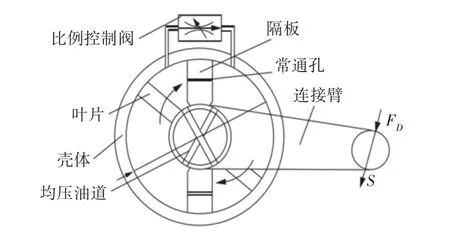
图1 可调叶片式减振器简化模型Fig.1 Simplified Model of Adjustable Vane Shock Absorber

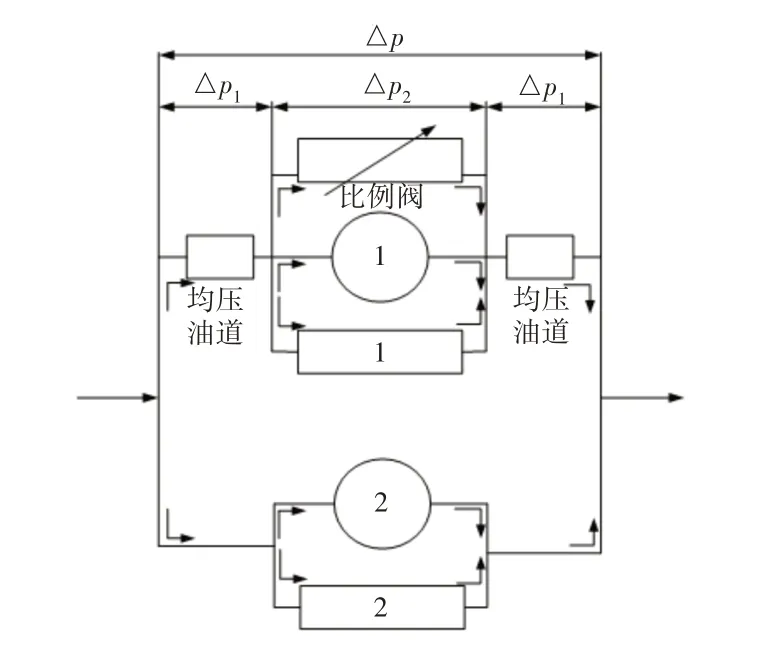
图2 可调叶片式减振器流体模型Fig.2 Fluid Model of Adjustable Vane Shock Absorber

对可调阻尼叶片式减振器流体模型的推导已经有成熟的研究，此处不再赘述，直接给出其阻尼特性模型公式。

式中：Q—减振器总流量；Q1、Q2—流经1、2两腔的流量；—减振器连接臂端速度；b—叶片工作高度；rb—减振器连接臂长度；Dw、Dn—工作腔外径、内径；Qv、Cv—比例阀的流量及流量系数；Qe、Ce—均压油道的流量及流量系数；∆p、∆p1、∆p2—流路中总压差、均压油道压差和1号流路压差。

2.2 基于深度置信网络的减振器逆模型

为通过所需阻尼力反求减振器所需控制电流的大小，建立了基于深度置信网络（DBN）的减振器逆模型。深度置信网络（DBN）是由n层受限玻尔兹曼机（RBM）和一个误差反向传播网络（BP）所构成的，其训练过程主要分为两步：预训练和微调。在这个网络中，通过RBM 网络训练模型的过程可以看作对一个深层BP 网络权值参数的初始化，因此DBN 克服了BP 网络因随机初始化权值参数而容易陷入局部最优和训练时间长的缺点。其网络结构图，如图3所示。其中w表示两层之间的权值。

图3 DBN结构图Fig.3 DBN Atructure Diagram

2.2.1 受限玻尔兹曼机

受限玻尔兹曼机RBM 是一种基于能量模型的随机神经网络，包括一个可视层和一个隐含层，且二者之间为全连接，以v和h分别表示可视层和隐含层中的节点值。

对于某一组具体的（v，h），其处于某个状态的概率由下式所决定［9］。

式中：vi、hj—可视单元i和隐含单元j；wij—两单元之间的连接权值；ai、bj—相应的偏置；θ—网络参数。由此，（v，h）的联合分布概率为：

式中：Z(θ)=—归一化因子。在知道可见层或隐含层的节点状态时，即可得到它们的条件概率函数：

反向传播神经网络被设置在DBN的最后一层，接收最后一层RBM的输出作为BP的输入向量，进行有监督的训练，从而对与训练阶段所产生的参数进行优化和微调。

2.2.2 数据集的采集

可调叶片式减振器在不同电流下的力-位移关系通过道路模拟试验台架测得，台架可给出不同振幅和频率的激振，并可测定对应的阻尼力和位移值，通过加装温度传感器，即可测定不同时刻减振器的温度。测试期间，改变减振器控制电流即可获得减振器在不同电流下的阻尼力特性。测试用道路模拟实验台架及控制台，如图4所示。

图4 道路模拟实验台架及控制台Fig.4 Bench and Console for Road Simulation Experiment

在试验过程中，分别设置电流为0A、0.5A、1A、1.5A、2A进行试验并采集数据。

为提高数据集中数据的有效性，在获取数据后需要对其进行滤波处理，并分别在处理后的数据中截取减振器平稳运行时的两段完整波形，最终共获取10000组数据作为数据集，随机取7000组数据作为训练集，另外3000组作为测试集使用。

2.3.半主动悬挂模型的建立

2.3.1 悬挂模型

针对车辆的俯仰运动和垂向运动建立其半车模型，出于简化考虑，忽略履带对车轮约束的影响，如图5所示。

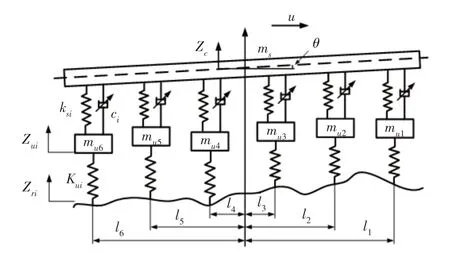
图5 半车模型Fig.5 Half Vehicle Model

其对应的履带车辆悬挂系统动力学方程为：

式中：Iy—车体转动惯量的一半；—俯仰角加速度；li—轮（1～6）相对于质心的水平距离，此外，对于上式中的zsi，应理解为每个车轮正上方车体对应的垂向位移，其与车身质心位移存在下述关系：

其中，li<0表示在质心后。

2.3.2 随机路面模型

在进行车辆平顺性仿真研究和性能评价时，需要获得准确的路面信息，国内外许多单位对路面不平度测量数据的研究表明，当车速恒定时，路面不平度服从Gauss概率分布，具有零均值的平稳各态历经特性，是以时间为参数的随机过程，不能用明确的数学关系表示。

当汽车以车速u驶过空间频率为n的路面时，路面随机高程位移随时间的变化函数为：

式中：n∞=0.011m-1—下截止空间频率；Gq(n0)—路面不平度系数，m3；W(t)—均值为0的Gauss白噪声；q(t)—路面随机高程位移。

3 半主动悬挂复合控制器设计

3.1 复合控制策略

复合控制策略主要分为三部分（:1）面向半车系统，主要指标为俯仰角、质心垂向加速度等多个指标的带约束的最优控制器；（2）面向单个悬挂系统的模糊控制器，这两个部分根据车身俯仰角的大小，通过S型分配函数实时进行权重系数的分配；（3）由减振器正逆模型构成的可调减振器系统，通过深度置信网络（DBN），根据期望阻尼力求解得到减振器的控制电流。这一复合控制策略的控制架构，如图6所示。

图6 复合控制策略架构Fig.6 Composite Control Policy Architecture

控制策略中权重系数函数按照S形函数进行分配：

对最终的控制输出，有：

式中：ucoc和ufuzzy—约束最优控制和模糊控制器的输出。

权重系数函数中的参数Sθ是一个控制权重变化速度的常数，θth—俯仰角的控制阈值。在这个控制策略中，取：

3.2 约束最优控制

由于半主动悬挂无法像主动悬挂一样产生主动作用的悬挂力，只能通过改变阻尼大小从而对阻尼力进行控制，因此在半主动悬挂的最优控制问题中，需要考虑阻尼力约束的影响。根据文献［10］，约束最优控制的表达式可写为：

式中：DFS—阻尼力约束（Damping Force Saturation），Uact—主动悬挂的最优控制表达式。对存在阻尼力约束的半主动悬挂约束最优控制有效性的证明方法在文献［10］中已经给出，此处不再赘述。

因此，要求解半主动悬挂的约束最优控制，需要先对主动悬挂的约束最优控制进行求解。

考虑到随机路面变化的特性，建立含俯仰角的半车系统的状态方程。分别选取系统的状态变量、系统输出、控制输入分别为：

干扰输入w为积分白声。

半主动悬挂的半车模型状态方程可以由如下公式表示：

式中：x∈R22，y∈R9，u∈R6，w∈R6，A∈R22×22，B∈R22×6，～B∈R22×6，C∈R9×22，D∈R9×6。各矩阵的具体表达式如下：

取最优控制性能指标为：

化为标准形式有：

其中各项系数矩阵满足：

确定加权系数后即可求解出矩阵Q，R，N，任意时刻下主动悬挂能够使性能指标最优的控制输入可表示为：

式中：最优控制反馈矩阵K=-R-1(BTP+NT)，且P满足代数黎卡提方程：

经多次调试，取q4～q9=1，q1=7304，q2=5037，q3=5590，r1～r6=0.0005。

3.3 模糊控制器设计

考虑到约束最优控制是建立在半车模型之上的，主要面向整车俯仰角和质心垂向加速度进行控制，对各轮处的针对性相对不足，因此根据单轮悬挂模型设计了模糊控制器。考虑到加速度信号变化较快，不易作为控制器的输入信号，因此输入变量采用悬挂动位移和悬挂动速度（动位移的微分），模糊函数使用高斯模糊函数，模糊变量分别设置为：

悬挂动位移X={NL，NB，NM，NS，ZO，PS，PM，PB，PL}；

悬挂动速度V={NL，NB，NM，NS，NZ，PZ，PS，PM，PB，PL}；

输出为半主动悬挂的阻尼值C={NB，NS，ZO，PS，PB}；

上述符号分别表示：

NL负极大，NB负大，NM负中，NS负小，NZ负零，ZO零，PZ正零，PS正小，PM正中，PB正大，PL正极大。NZ和PZ是为了在接近零点时增加分辨率而设置的，也是描述变量的一个区域。这个模糊控制的规则，如表1所示。

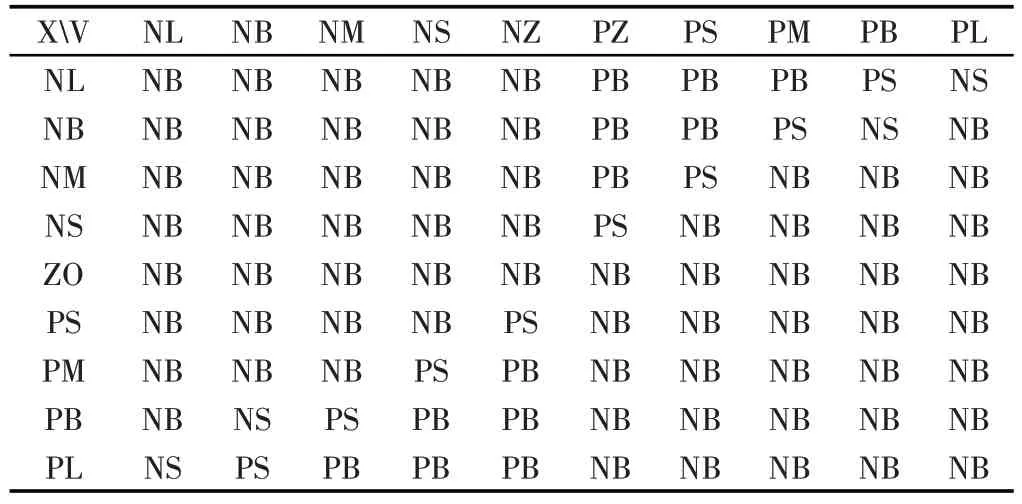
表1 模糊控制规则Tab.1 Fuzzy Control Rules

4 仿真验证

在数据集中随机取得3000组数据作为测试集进行DBN模型的验证，预测结果及真实值，如图7所示。预测值及真实值之间的误差，如图8所示。从测试结果来看，DBN对于测试集的分类和预测结果良好，预测误差基本在（-0.06～0.07）A以内，这可以表明，DBN逆模型能够较好的对数据进行分类和预测。

图7 测试集预测结果Fig.7 Test Set Prediction Results

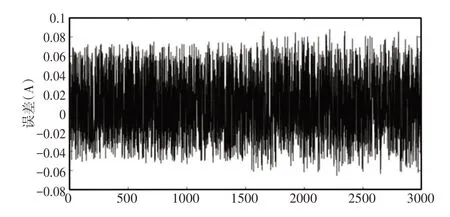
图8 测试集预测误差Fig.8 Test Set Prediction Error

复合控制策略整体的仿真验证采用20m/s的速度通过F级路面，并在Simulink里建立了仿真模型，系统内各参数数值设置，如表2所示。

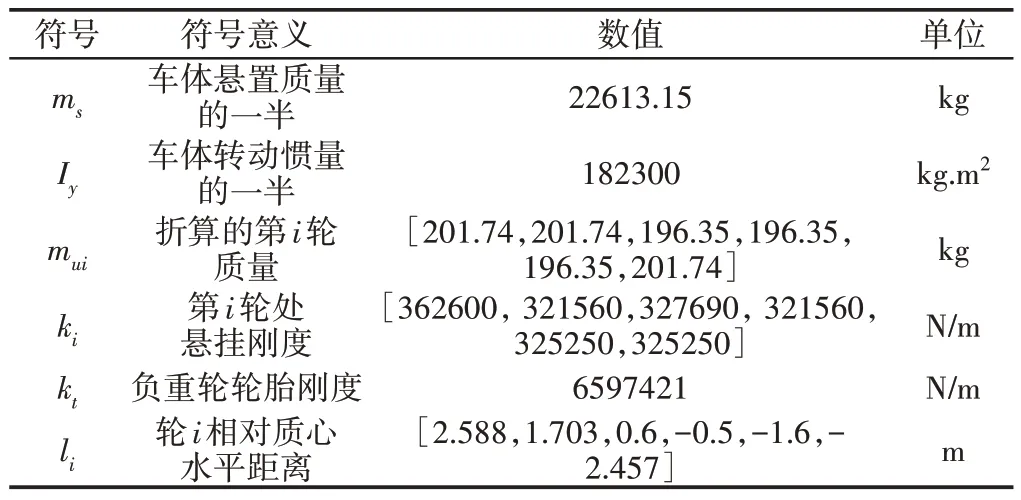
表2 模型参数符号、含义及赋值表Tab.2 Model Parameter Symbol，Meaning and Assignment Table

通过仿真得到了各轮悬挂的控制力和悬挂动位移，半车模型质心处的垂向加速度以及俯仰角，悬挂质心处的垂向加速度和俯仰角，如图9、图10所示。

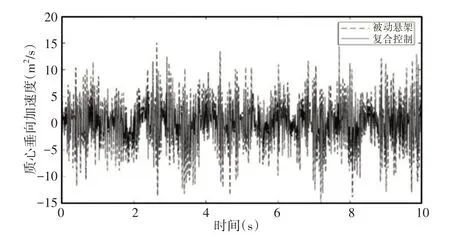
图9 质心垂向加速度对比Fig.9 Vertical Acceleration Comparison of Center of Mass

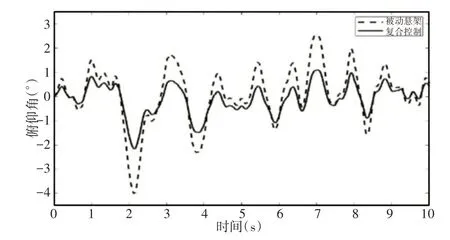
图10 俯仰角对比Fig.10 Comparison of Pitch Angles

选取轮1处对应的悬挂控制力、悬挂动位移、悬挂总阻尼力和期望的阻尼增加值列出，如图11所示。需要注意的是，图中半主动悬挂的控制力在实际情况中应体现为通过电流改变而使悬挂阻尼变化的值。可以看出，在复合控制策略的介入下，质心处的垂向加速度均方根值由4.526下降至3.107，下降了31.35%，俯仰角最大值由4.0094°下降至2.1604°，均方根值由1.1759下降至0.6746，下降了42.63%，同时各轮处的悬挂动位移略有降低。

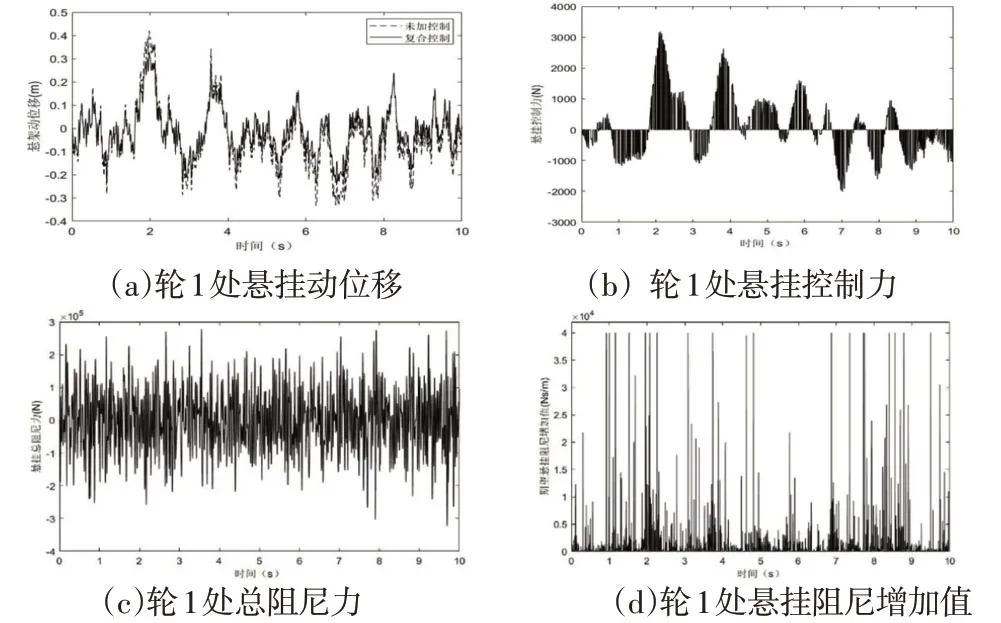
图11 轮1处悬挂各项参数仿真Fig.11 Simulation of Various Parameters of Suspension at Wheel 1

综上所述，所提出的半主动复合控制策略对于车辆悬挂的性能有一定的优化和提升，能够有效提高车辆的舒适性和安全性。

5 结束语

建立了一个分层的半主动悬挂控制策略，首先根据台架试验的数据建立了深度置信网络逆模型，然后分别根据半车模型和单轮模型，进行了约束最优控制器和模糊控制器的设计，并通过S函数进行权重分配，最终得到复合控制的阻尼力输出。在Python和Matlab/Simulink 环境中搭建了虚拟试验平台，对这一复合控制策略进行了仿真，仿真结果表明，该复合控制策略能够有效降低质心垂向加速度和俯仰角，且对各轮处对应的悬挂动位移也有一定的改善效果，说明该控制策略能够有效提升车辆的舒适性和安全性。