基于代理模型的索卡减重优化设计

解 昊，王林涛，郑首坤

（大连理工大学机械工程学院，辽宁 大连 116024）

1 引言

架空缆道是由支撑和运载设备组成的一种便利的高空运输工具［1］。与传统地面运输工具相比，架空缆道具有适应性好、运输效率高、机械化，自动化程度高等优点。因此，架空缆道在我国的煤炭、冶金、农林、旅游等地形复杂行业得到了日益广泛的应用。

架空缆道的核心设备—索卡是由内索卡，外索卡，主轴，弹簧装置，销轴，摩擦板，辅助轮和行走轮组成，作为连接钢丝绳和吊箱的部件，在架空缆道中发挥着至关重要的作用，如图1所示。由于我国的架空缆道设计标准并不完善，设计人员只能参考以往经验选用过大的安全系数，容易造成过设计降低缆道的经济性。因此，有必要在满足强度、稳定性条件下对索卡进行结构优化设计。

图1 索卡结构Fig.1 Rope Clip Structure

针对索卡的结构设计国内有如下研究。文献［2］设计了一种双侧同心螺旋弹簧脱挂索卡，并利用有限元法对结构关键部位进行校核。文献［3］对国外四杆机构索卡进行改进，并验证了新结构的可行性。文献［4］对重力式索卡进行优化，解决工程中遇到的问题，并利用有限元法验证了新结构的强度和稳定性。文献［5］提出了一种铰杆增力机构索卡，并利用MATLAB 对该结构的夹紧力进行优化。这里把研究重点放在索卡的核心部件—内索卡和外索卡，探究在满足设计规范的前提下，对结构进行减重优化。

传统的结构优化问题主要是借助有限元仿真来完成，虽然通过此方法可以获得精确的优化结果，但也存在耗时过长导致效率较低的问题［6］。在此背景下，工程中经常用易于计算的代理模型来解决这种复杂的黑箱问题［7］。在代理模型研究方面，目前已经发展了包括多项式响应面（RSM），Kriging 函数，径向基函数（RBF），支持向量回归（SVR）等多种代理模型方法。Kriging模型由于对高维非线性问题具有良好的近似能力和独特的误差估计被越来越多地应用在工程中［8］。下文将分为建立参数及有限元模型，构建Kriging模型以及优化求解三个部分进行叙述。

2 建立参数及有限元模型

2.1 参数模型

利用建模软件建立索卡核心部件的三维模型。如图2所示。图中分别为内索卡、外索卡、钢丝绳和轮衬。在满足装配条件的前提下对内索卡选取18个参数，对外索卡选取16个参数，有6组参数存在关联，最终作为独立变量的参数共有28个。设计变量的基本信息，如表1所示。

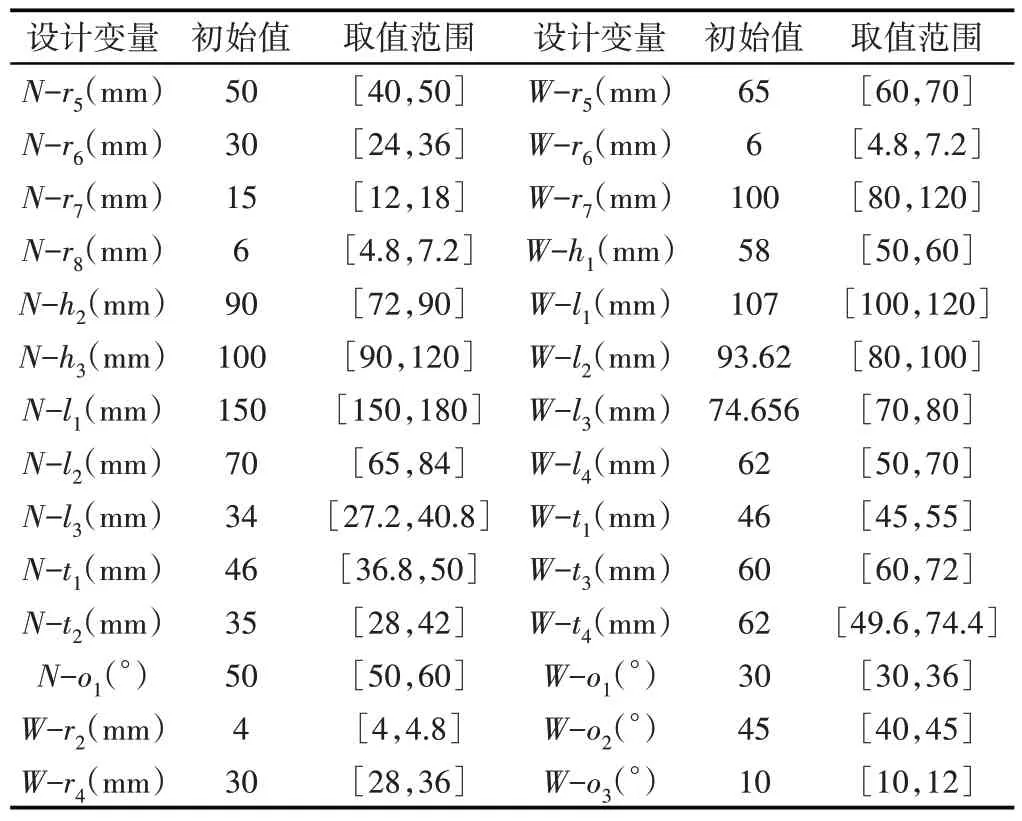
表1 设计变量Tab.1 Design Variables

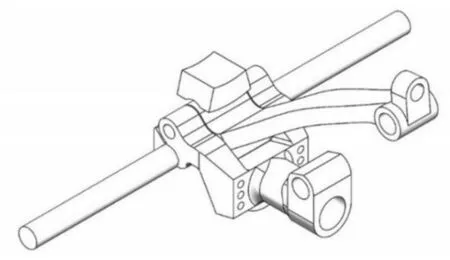
图2 索卡三维模型Fig.2 3D Diagram of Rope Clip

2.2 有限元模型

2.2.1 载荷分析

索卡的载荷来自三个方面：吊箱的重力，弹簧力，风载。吊箱自重（含索卡）为7080N，最多允许承载8人，每人约重740N。弹簧通过预压缩安装在索卡上用于提供夹紧力，防止吊厢在爬坡时发生下滑。

风载总是作用于吊箱上且与运动方向相反。具体的载荷信息及作用位置，如表2所示。

表2 载荷信息Tab.2 Load Information

2.2.2 建立有限元模型

将图2中的参数模型导入ANSYS Workbench进行静力学和模态分析。钢丝绳在线路中被视为柔性体，因此定义为各向异性材料，模型各部位的材料，如表3 所示。对模型进行网格划分，内、外索卡由于形状复杂故采用8mm 四面体网格，危险部位用1mm网格进行加密，钢丝绳和轮衬采用8mm六面体网格，共生成单元数108051，节点数246645。钢丝绳与内、外索卡的夹口设为摩擦接触，摩擦系数0.3。轮衬与外索卡同样设为摩擦接触，摩擦系数0.1。建立与内索卡耦合的远端点来模拟吊箱，将吊箱重力与风载施加到远端点。钢丝绳在线路中的张紧力为350kN，经过轮衬时会发生1°的弯曲。将载荷施加到模型对应位置，约束轮衬上端面和钢丝绳中面，有限元模型及分析结果，如图3所示。

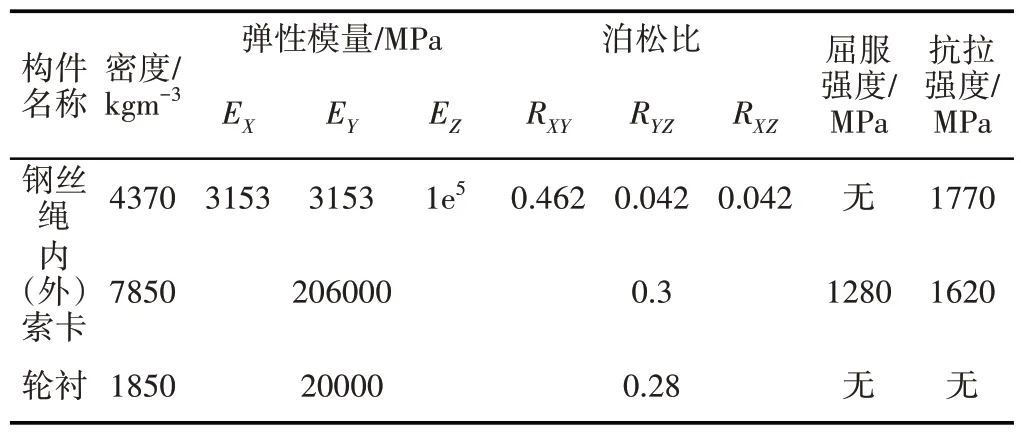
表3 材料属性Tab.3 Material Properties

图3 有限元模型及分析结果Fig.3 Finite Element Model and Analysis Results

3 构建代理模型

在优化过程中，使用有限元模型迭代求得最优解往往耗时较长，效率极低。因此，有必要建立内索卡和外索卡的代理模型。考虑到高维非线性的拟合能力和精度分析，因此选择构建Kriging代理模型。

首先需要建立样本空间（S，y）s，其中S=[x(1)，x(2)，…，x(n)]T，表示抽样获得的n组设计变量；ys=[y(x(1))，y(x(2))，…，y(x(n))]T，表示每组设计变量对应的有限元仿真响应值。Kriging模型［8-9］是一种插值模型，其插值结果为已知样本函数响应值的线性加权：

为计算权系数引入假设：将未知函数看成是某个高斯静态随机过程的具体体现。静态随机过程定义如下：

式中：β0—Y（x）的数学期望；Z（x）—均值为0，方差为σ2的高斯分布。样本空间中变量间的相关性可以表示为：

基于上述假设，可计算出Kriging模型最优加权系数ω，使得预测的均方差

最小，并满足预测的无偏估计性：

利用拉格朗日乘数法求得模型的预测值和均方差：

式中：F—各元素均为1的列向量；

最后通过求解最大似然函数公式获得θ和σ2完成模型的构建：

为了保证Kriging模型有较高的精度，应使训练样本尽量充满样本空间。在此，利用最优拉丁超立方筛选600个训练样本，利用拉丁超立方筛选500个测试样本。以预测值和真实值的相关系数r2作为衡量模型精度的标准，通常要求r2≥0.95。

最终，构建出内索卡和外索卡的质量、最大应力、一阶固有频率和二阶固有频率的Kriging模型，六个模型预测值和真实值的对比情况，如图4 所示。从结果可以看出，六个模型均满足r2≥0.95的精度要求。

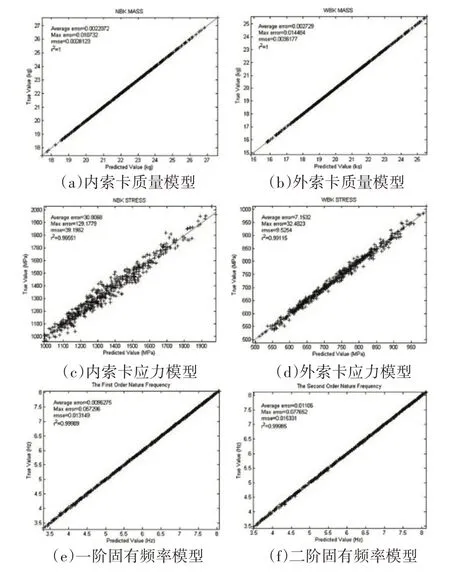
图4 Kriging模型Fig.4 Kriging Surrogate Model

4 优化结果

4.1 优化方程

代理模型构建完成后即可进行后续的优化工作。内、外索卡的材料选用合金钢35CrMnSiA，屈服强度为1280MPa，根据设计规范取安全系数为1.35得到材料的许用应力［σ］=948MPa，要保证内索卡最大应力σN和外索卡最大应力σW不超过许用应力［σ］。缆道在运行时会使钢丝绳产生激振响应，这种周期性的激振频率f=3.2962Hz［5］。

为了避免共振，设计中要求固有频率与激振频率应相差15%到20%。因此规定一阶固有频率f1和二阶固有频率f2均不超过0.85f或不低于1.15f。综上所述，以内索卡和外索卡的总质量为优化目标，优化方程可以表示为：

式中：x—设计变量组成的向量，共28个元素；xD、xU—变量的下限和上限。

4.2 优化求解

优化方程确立后，需要选择合适的优化算法对方程求解。为了获得高精度的全局最优解，这里选用MIGA（多岛遗传算法）与NLPQL（非线性二次规划）相结合的优化算法［10］。MIGA 是对并行分布遗传算法的改进，具有优良的全局求解能力。同时，NLPQL具有很强的局部搜索能力和搜索效率。

在Isight中将两种算法结合，首先应用MIGA 定位目标极值在设计空间中所处的区域，再应用NLPQL对该区域进行精确寻优，以获得最终优化结果。

优化目标和约束的收敛过程，如图5所示。分为MIGA全局寻优和NLPQL局部寻优两部分。

图5 优化过程收敛曲线Fig.5 Convergence Curve of Optimization

可以看出，优化目标收敛于33.16kg，g1中的σN收敛于947.96MPa，g2中σW的收敛于625.51MPa，g3收敛于-18.87，g4收敛于-19.36。优化过程的初始值和最终结果，如表4所示。

从表中可以看出，经过MIGA求解之后，与初始值相比内索卡应力减少了9.51%，外索卡应力增加了5.54%，一阶固有频率约束增加了40.01%，二阶固有频率约束增加了39.15%，内、外索卡的总质量增加了4.47%，从42.54kg变为44.44kg。经过NLPQL求解之后，与初始值相比内索卡应力减小了8.8%，外索卡应力减小了6.32%，一阶固有频率约束增加了20.42%，二阶固有频率约束增加了19.72%，内、外索卡的总质量减少了22.05%，从42.54kg变为33.16kg，减轻了9.38kg。

将优化后得到的设计变量取值代入有限元模型进行分析，计算仿真结果与优化响应值的相对误差具体，如表5所示。验证优化过程的准确性。可以看出，NLPQL优化结果的相对误差分别为0.21%，5.27%，-0.37%，-0.31%和0.03%。虽然外索卡应力的相对误差偏高，但结果显示，约束g2已经大大远离约束边界，不会因为误差造成约束失效。综上所述，Kriging模型精度较高，优化结果可靠。

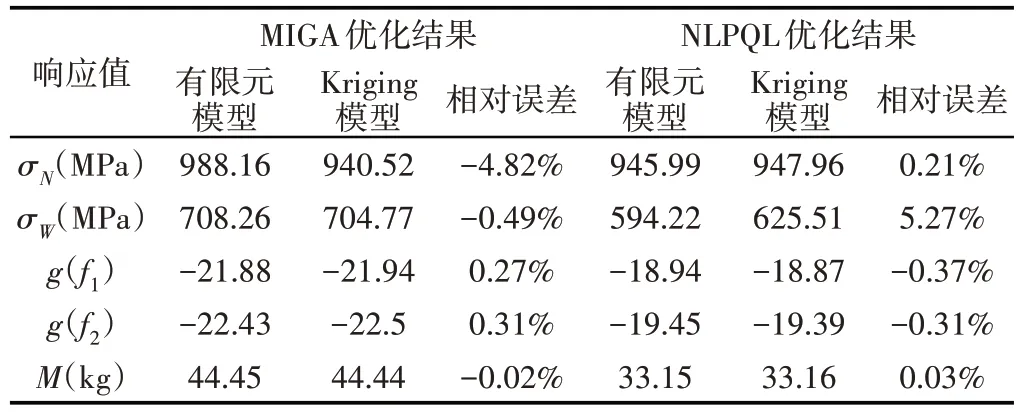
表5 误差分析Tab.5 Error Analysis

5 结论

这里以内索卡和外索卡的总质量为优化目标，通过建立Kriging 代理模型来解决有限元仿真优化效率低的问题，利用MIGA和NLPQL相结合的优化算法来获得高精度的全局最优解。优化结果显示，索卡总质量减轻了22.05%，Kriging模型与有限元模型的最大相对误差为5.27%，说明代理模型可以有效代替有限元模型来解决工程中的优化问题。