基于尺寸优化的电铲斗杆轻量化设计

谭 磊，孙 刚，王永富

（1.矿山采掘装备及智能制造国家重点实验室，山西 太原 030024）（2.东北大学机械工程与自动化学院，辽宁 沈阳 110819）

1 引言

电铲也称机械式挖掘机，是露天煤矿开采的专用设备之一，主要用于采掘矿石和装载工作。斗杆是机械式挖掘机工作装置的主要构件，主要由质量较大的箱型结构组成，并且斗杆也在机械式挖掘机工作装置的前端，其质量对电铲运行性能以及稳定性影响较大，因此斗杆轻量化对于降低生产成本和提高机械式挖掘机的工作效率至关重要[1-3]。

早期的电铲斗杆设计主要是由设计人员根据经验和类比等方法对斗杆进行结构设计，为了提高安全性，设计的斗杆结构材料一般未得到完全充分利用，使得整体质量较大。随着轻量化和CAE技术的飞速发展，电铲斗杆的轻量化主要分为拓扑优化和尺寸优化，其中拓扑优化是对斗杆的形状和材料的空间分配进行优化设计，而考虑到拓扑优化对斗杆质量的减轻不显著，因此在满足设计应力和形变的条件下采用尺寸优化对电铲斗杆的最小质量进行求解从而达到减轻斗杆质量的目的[4-5]。

由于斗杆的外部箱体结构的尺寸以及内部加强筋的尺寸均不一样且对应力的影响较大，故将以上多个尺寸作为设计变量，且对最小斗杆质量的影响是不一致的，有相互约束和相互矛盾的关系，为了实现降低斗杆质量的目标，应运用多目标优化方法对电铲斗杆响应面模型进行优化设计。

2 电铲斗杆的力学模型

2.1 建立斗杆三维模型

电铲斗杆结构的三维模型由UG建立，由于斗杆零部件结构复杂，为了减小有限元出错几率和计算量，在满足斗杆工况的前提下，对斗杆模型进行简化，去掉细小特征如螺纹孔、细小圆角等，简化后的三维模型，如图1所示。

2.2 对斗杆尺寸参数化

一般来说，取的设计变量越多，计算的结果就越准确，但相应的计算的工作量就越大。在实际工作中，设计变量都尽可能的取少，选择斗杆上下钢板厚度为一组，两侧钢板厚度为一组以及内部加强筋厚度为一组进行参数化定义，每组厚度变化保持一致，变化范围为相应厚度初始值的10%。在UG 中通过参数化模块，根据Ansys Workbench 的参数设置识别码“DS_”进行参数化设置。

第一组上下钢板厚度初始值为25mm，参数化DS_P171，变化范围为（22.5～27.5）mm，如图2所示。

第二组两侧立板厚度初始值为25mm，参数化DS_P1601，变化范围为（22.5～27.5）mm，如图3所示。

第三组内部加强筋厚度初始值为12mm，参数化DS_P193，变化范围为（10.8～13.2）mm，如图4所示。

2.3 工况及力学计算

在分析挖掘机工作装置受力时，一般都是针对最危险工况。计算中选用最危险工况是：当动臂处于倾角45°，斗杆中心线和地面平行，此时斗杆正常伸出，挖掘处于推压轴高度的矿岩，满斗遇到障碍物，此时提升力达到最大值，斗杆所受弯矩接近最大值[1]，如图5所示。

图5 斗杆受力图Fig.5 Sketch Map of Stick Under the Force

横向力Ft1是机械式挖掘机处于挖掘状态时，障碍物施加在斗杆上的横向作用力：

式中：Ft1—横向力；M—电铲回转机构中制动器制动力矩；i—从制动器到齿圈的传动比；rm—斗杆回转中心线到推压齿轮与斗杆接触点A的水平距离；rn—推压齿轮与斗杆接触点A与斗杆齿尖水平距离；η1—电铲回转机构的转动效率是0.97。

Ftq是最大提升力，由提升机构提供：

式中：Ftq—最大提升力；J1—提升机构提升电机过载系数；Pl1—提升机构的提升电机最大功率；ηl1—提升机构传动效率；ηl2—天轮传动效率；vls—卷筒钢丝绳速度。

Ft2是由机械式挖掘机推压电机提供的最大推压力，根据式（3）获得：

式中：Ft2—最大推压力；J2—推压电机过载系数；Pl2—推压电机最大功率；ηl3—推压机构传动效率；vts—推压速度。

由斗杆、铲斗以及满斗物料质量可知：

式中：Gi—分别表示铲斗重力、斗杆重力，满斗物料重力，其中i取1、2、3；Mi—表示质量；g—重力加速度。

Ft4是铲斗齿尖法向挖掘阻力，根据水平方向二力平衡可得：

Ft3是铲斗齿尖切向挖掘阻力，Ft5是斗杆推压轴处反力，根据斗杆受力平衡和力矩平衡可得：

式中：F(k)—对A点取距计算时方向为顺时针的第k个力；F(j)—对A点取距计算时方向为逆时针的第j个力；n—对A点取距计算时方向为顺时针力的个数；h—对A点取距计算时方向为逆时针力的个数；rk、rj—A点到F(k)、F(j)的力臂；Ft1—横向力；Ft2—最大推压力；Ftq—铲斗提升力。

式中：F(l)—和Ft5方向相反的第l个力；F(k)—和Ft5方向相同的第k个力；n—和Ft5方向相反的个数；m—和Ft5方向相同的个数；Ft4—法向挖掘阻力；Ftq—铲斗提升力；Gi—分别表示铲斗重力、斗杆重力、物料重力，其中，i取1、2、3。

将已知数据带入式（1）～式（7），得出危险工况下对斗杆需施加的载荷，如表1所示。

表1 斗杆载荷表Tab.1 Load of Stick

3 电铲斗杆的有限元分析

在ANSYS Workbench中的静力学分析模块中直接导入简化后的三维模型，设置斗杆的材料为Q345，材料的主要属性，如表2所示。

表2 材料主要参数Tab.2 Main Parameters of Material

采用四面体法和六面体法对导入的斗杆三维模型进行划分。为了保证工作效率和应力计算，网格大小控制在50mm 左右，对模型网格划分结束后，共有76679 单元，245446 个节点，如图6所示。

图6 斗杆划分网格图Fig.6 Stick Grid Diagram

对斗杆施加边界条件，在实际工作中，铲斗与斗杆之间没有相对运动，故在斗杆与铲斗连接的轴孔处用Fixed support限制所有自由度并按照载荷表1施加载荷，如图7所示。

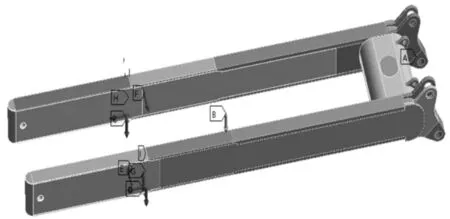
图7 斗杆施加边界条件图Fig.7 Diagram of Stick Applied Boundary Conditions

对斗杆有限元模型施加全约束以及施加载荷后，对模型的总应力和总形变求解，得到结果，如图8 所示。由图8（a）、8（b）可知，在恶劣工况下，斗杆最大应力为207.31MPa，最大变形为49.013mm。

图8 斗杆静力学分析图Fig.8 Stick Statics Analysis Diagram

4 电铲斗杆的尺寸优化

4.1 尺寸优化数学模型

尺寸优化是指在一定的约束和边界条件下，利用一定的算法找到目标函数的最优解的设计方法，一般能够达到减轻质量和节省生产材料的目的。以斗杆静力学分析结果为基础，采用响应面分析法进行斗杆的尺寸优化达到减轻斗杆质量的目的[6-7]。其具体优化流程，如图9所示。

图9 斗杆优化设计过程Fig.9 Topological Optimization Flow Chart

响应面法具有结构简单、计算量小、计算方便、收敛快等特点，选取工程实践中常用的二阶多项式响应面法：

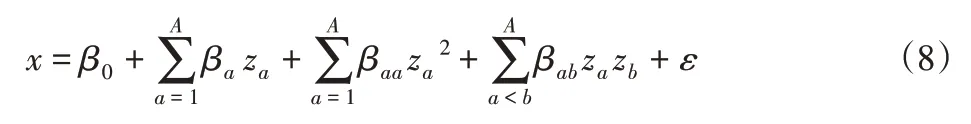
式中：x—响应函数；za，zb—第个设计变量；β0、βa、βaa、βab—回归系数；ε—回归系数；A—设计变量的个数。

斗杆轻量化优化问题，是减少斗杆质量的同时还要保证其承受的最大应力不超过材料的许用应力，是个多目标优化的问题。

多目标最优化法是通过某一约束来寻求多个目标函数的最优解的问题。根据分析云图可知，斗杆的上下钢板厚度，两侧立板厚度以及内部加强筋厚度对最大应力和质量影响较大，故将以上三个参数设置为变量，将斗杆的最大应力设置为约束条件，将斗杆的最小质量设置为目标函数。

综上可得出优化数学模型如下：

式中：f(x)—目标函数，即斗杆质量最小；—设计变量xi的上下限；[σ]—斗杆的材料Q345的许用应力值；σs—最大应力。

4.2 响应面分析法优化

利用Ansys Workbench的RSO模块进行优化，在进行响应面分析前需要定义目标参数、设计变量和约束参数，参数设置完成后，采用Central Composite Design 设计实验点，共生成了15个设计实验点，结合定义的响应面模型的约束参数，进行斗杆轻量化的计算，计算结果，如图10所示。

图10 部分优化设计点计算结果Fig.10 Partially Optimized Design Point Calculation Results

根据优化设计的结果，结合灵敏度分析，可知DS_P1601相较于其他两组设计变量对斗杆的质量影响最大，DS_P171对斗杆最大应力影响最大，如图11所示。为了更好的理解设计变量与目标函数之间的相关性，还可以使用三维响应曲面图分别描述DS_P1601与DS_P171对斗杆质量P16和斗杆最大应力P17的关系，如图12所示。

图11 斗杆灵敏度分析图Fig.11 Stick Sensitivity Analysis Chart

图12 斗杆响应曲面图Fig.12 Stick Response Surface Plot

由斗杆尺寸优化结果可知：电铲斗杆优化后最小质量为19635kg，斗杆最大质量为21338kg。

4.3 响应面分析法优化

通过Workbench软件对斗杆的模型进行仿真优化，优化结束后得到三组候选设计点，如表3所示。对比三组候选点后可知，方案C相较于其他两种方案的最大应力值更小，斗杆质量结果更优。故选择方案C为最优设计方案。

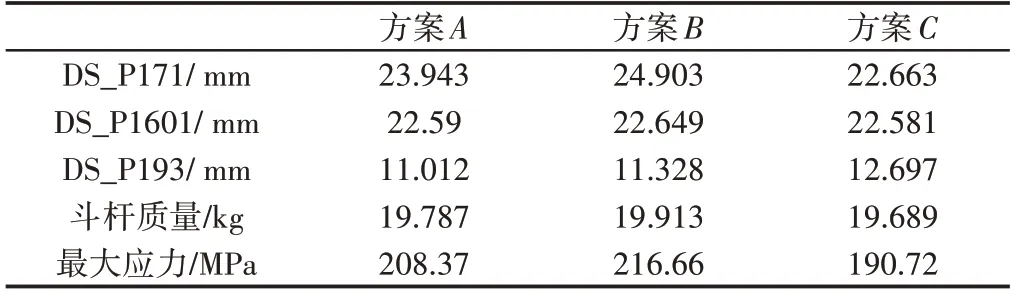
表3 优化设计候选方案Tab.3 Optimize Design Candidates

考虑加工工艺以及材料实际使用规范，对方案C的尺寸进行圆整，圆整后的数据，如表4所示。

表4 圆整后数据Tab.4 Data After Rounding

4.4 电铲斗杆优化后的对比分析

将方案C圆整后的数据作为最优设计点插入，更新设计点之后，其总形变和总应力结果，如图13所示。

图13 优化后斗杆形变量与应力云图Fig.13 Displacement &Stress Cloud Chart of Optimized Stick

分析表5可知，在相同的工况下，优化后斗杆的形变量改变不大，但最大应力和质量都有显著的降低，不仅满足了斗杆的强度等性能要求，而且达到轻量化的目的。

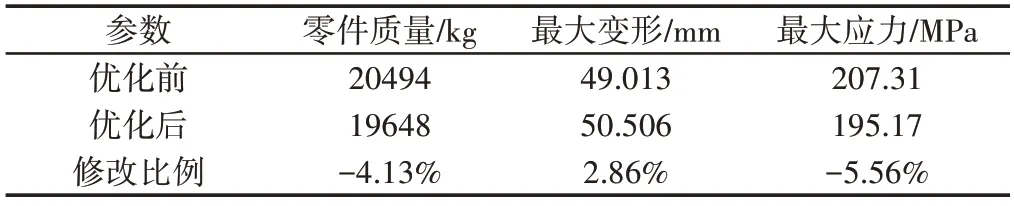
表5 优化结果分析比较Tab.5 Comparison of Previous &Optimized Stick

5 结论

以斗杆为研究对象，运用UG对其参数化建模，确定危险工况并对此工况进行力学计算。采用Ansys Workbench 对斗杆进行静力学分析，得到在危险工况下的应力、形变图。基于静力学分析的结果，采用响应面分析法，以斗杆关键尺寸为设计变量，以斗杆最小质量为优化目标，在得到的15组数据中，得到最优设计方案。最后，在相同的工况下以及满足应力和形变的前提下，将优化前的初始方案和最优方案对比，结果显示轻量化前后斗杆质量分别为20494kg和19648kg，其质量减轻了4.13%，达到了斗杆轻量化的目的，节约了生产成本。