6R模块化机器人逆解算法与误差分析

刘广瑞，孟少飞，王 钊，高建设

（郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

6R机器人是一个集成度很高的机电一体化产品，运动学是其研究的首要前提，包括正逆运动学，而逆运动学求解的精度、泛化能力、实时性等是机器人进行轨迹规划和离线编程的基础，机器人的逆运动学模型是一个多输入多输出系统，其逆运动学方程具有高维、非线性的特点，求解复杂且不易求出。

许多学者对6R 串联机械臂的逆运动学研究做了很大的贡献[1-3]，例如解析法，几何法和数值迭代法等。解析法虽然可以得到全部解，但计算过程较复杂；几何法只能简化某些特殊的结构，通用性较差；迭代法具有通用性，但却无法得到全部的解，且存在迭代时间长和迭代不收敛的情况，进行实时控制时可靠性低。

神经网络作为一种智能算法，能在一个有限的集合内和任意精度下逼近任何非线性函数，影响网络的收敛精度主要有两个因素，训练样本的质量、网络的结构参数。

不少学者运用神经网络对机器人逆运动学求解方面进行了研究工作，训练样本采集主要为运动学正解和实验获取两种途径。

文献[4]采用RBF 网络研究了SCARA 机器人逆解问题，训练样本通过对关节角取等间隔获得，虽取得了满意结果，但精度和泛化能力仍需提高。

文献[5-6]分别采用RBF网络和MFBP网络研究了机器人逆解问题，虽然逆解角度取得了不错的效果，但对样本筛选处理的算法过程过于复杂，由于逆解多解的存在，剔除矛盾样本时人为干扰因素较多，增加了逆解求解的难度和时间周期。

文献[7]采用BP网络研究了自主研发的6R机器人逆解问题，取得了满意的结果，但训练样本通过实验获取，浪费大量精力，且样本容量较小，训练的网络泛化能力较差。

不难看出，单独的用解析法、几何法、数值迭代法进行机器人逆运动学求解具有一定的局限性，虽然神经网络在机器人逆运动学中取得了一定的成就，但由于机器人逆解多解和奇异性问题使得在神经网络求解的精度、泛化能力、筛选训练样本算法的问题上仍有进一步的提升空间。

因此为了提高求解的精度和缩短逆解求解的时间周期，这里采用解析法与BP神经网络相结合的方法求解6R模块化机器人逆运动学，解析法求解前几个关节逆解，其余使用BP神经网络预测求逆解，即（q解析+BP，q=0,1…6）通过使用不同的组合模式，仿真对比发现，3解析+BP组合模型求解精度比其它组合模式具有更高的精度，较强的泛化能力，且缩短了求逆解的时间周期，该求逆解模型为6R机器人求逆解提供了新的思路和方法。

2 6R模块化机器人正运动学分析

2.1 结构参数建模

机械臂正运动学求解是已知机械臂各关节角度，求取机械臂末端手抓在基坐标系下的期望位姿，6R机器人的前三个关节角度确定手腕参考点的位置，后三个关节角度确定手腕的姿态，根据机器人的结构参数和外形尺寸，运用D-H法建立各个关节的坐标系，其结构示意图和各连杆变换坐标系，如图1所示。

相邻两连杆坐标系的齐次变换矩阵为；

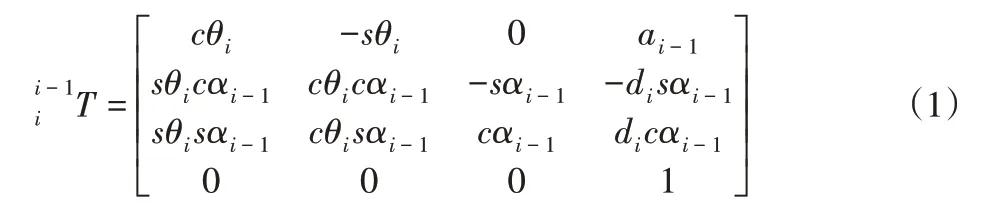
式中：ai-1—连杆的长度；αi-1—扭角；di—偏置；θi—关节角。其中：ci=cos(θi)，si=sin(θi)。

6R模块化机器人的D-H参数表，如表1所示。

表1 6R模块化机器人D-H参数Tab.1 D-H Parameters of 6-R Modular Robot

2.2 正运动学解算

根据相邻连杆坐标的齐次变化矩阵，机器人末端相对于坐标系0的位姿矩阵为：

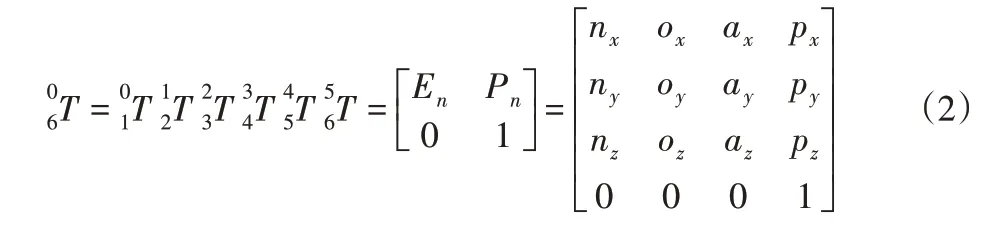
式中：En—机器人末端姿态；Pn—机器人末端位置。

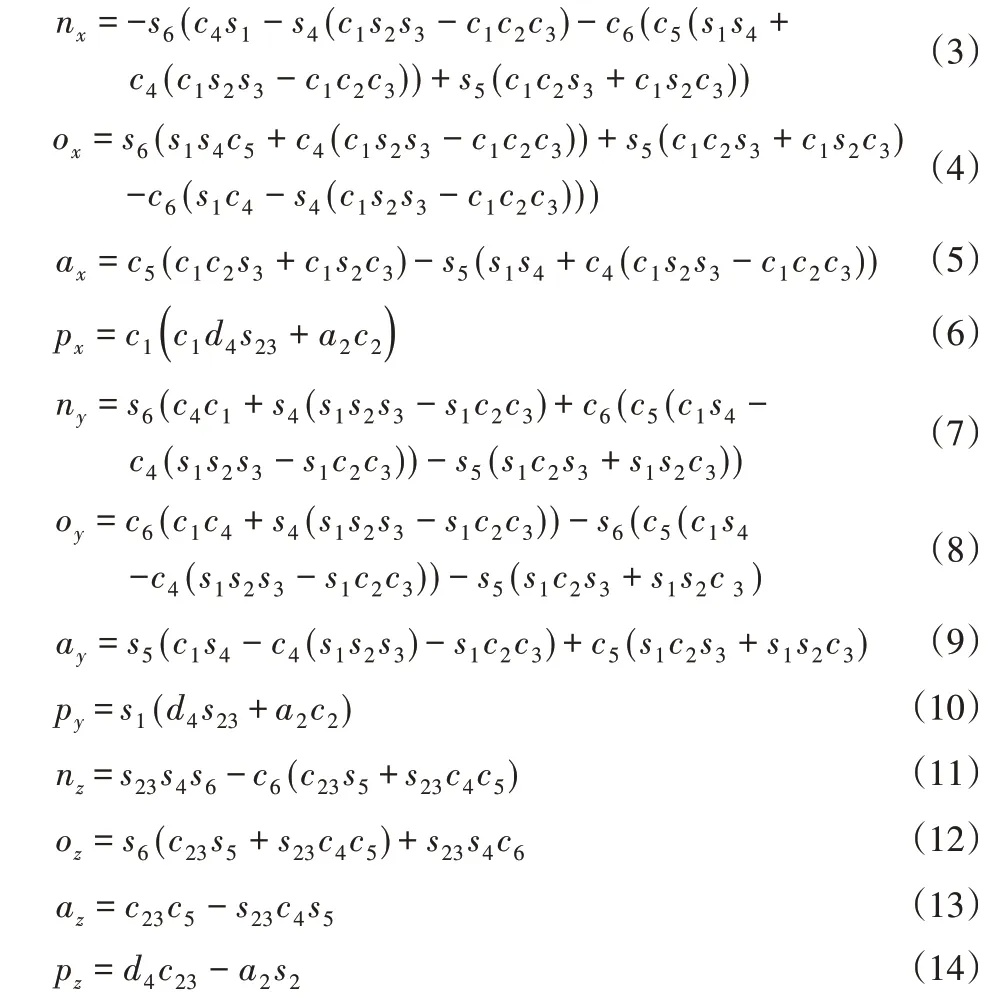
式中：sij=sin(θi+θj)；cij=cos(θi+θj)。

机器人作业时是已知手抓工具末端的位姿矩阵，而求逆解需知机器人末端的位姿矩阵即：

上式对机器人直接求逆是非常困难的，需要对12个非线性方程进行求解，由于神经网络可以预测非线性系统，因此采用解析+BP神经网络相结合的方式求逆解。

网络训练时为了减小网络结构负担，把机器人末端姿态变量En转化为绕固定轴x-y-z变化的RPY角，根据坐标转换原理可得末端姿态En的RPY角为：

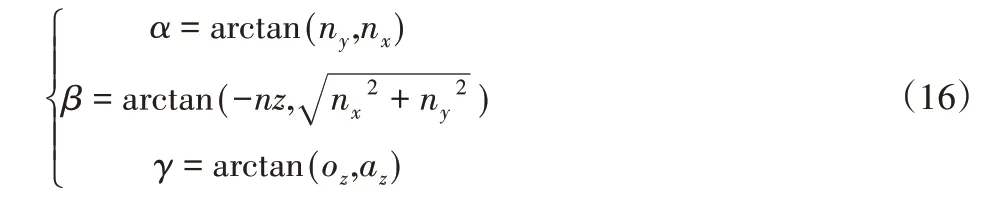
根据文献[8]可知，采用解析法求解时，后一个关节角的求解需在前一个关节角的求解基础之上，随着解析解求关节角度个数的增加，求解算法越来越复杂，前三个关节确定机器人位置，后三个确定姿态，求机器人前三个关节角度比后三个关节角度简单许多，所以qmax=3。

针对大部分6R机器人，如PUMA560、IRB120等，多解一般产生在前三个关节，当q=3时，对神经网络训练样本进行筛选，简化了逆解多解的问题，减少了矛盾样本的容量，从而缩短了筛选样本的时间周期，因此当q=3时，该逆解组合求解模型较优，计算周期最短。以下主要讨论3解析+BP组合模型的求解过程。

3 逆运动学求解

该机器人最后三个关节轴线交于一点，满足Pieper准则，存在封闭解。由于直接求解12个非线性方程组较为复杂，所以根据机器人末端位姿用解析法求前三个关节角度，从而得到的位姿，根据齐次矩阵变换原理得到手爪末端相对于第三个关节坐标的位姿变化矩阵为：

接下来用BP神经网络对后三个关节角度进行预测。

3.1 求解θ1、θ2、θ3

令式（22）两边的（1，4）、（2，4）元素分别对应相等有：

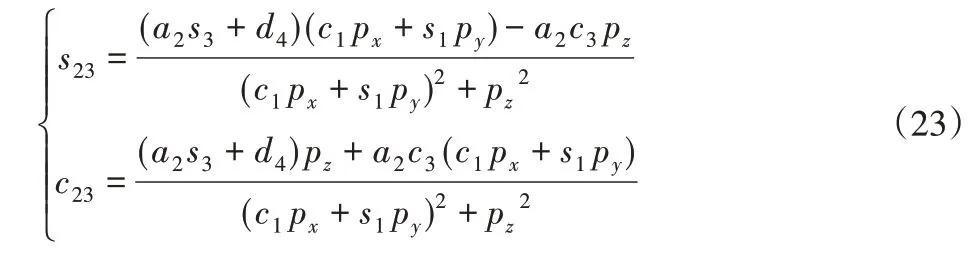
因此求出关节2、3的角度和：

当选中关节3的一组解后，关节2的角度也随之确定，即：

3.2 求解θ4、θ5、θ6

BP 神经网络是一种按误差逆传播算法训练的多层前馈网络，学习规则使用最速下降法，通过反向传播不断调整网络的权值和阈值，使网络的误差平方和最小。网络模型拓扑结构包括输入层，隐含层，输出层，其结构，如图2所示。

网络的输入为机器人手抓末端位姿变量α、β、γ、Px、Py和Pz，网络的输出为机器人各个关节角，网络的输入和输出的关系为：

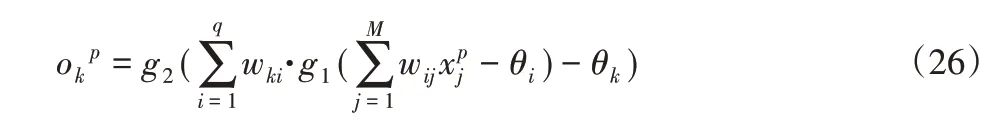
式中：—输入层第j个神经元在样本p作用下的输入(j，p=1，2，3…M)；Wij、θi—输入层到隐含层的权值和隐含层的阈值(i=1，2，3…，q)；g1—隐含层的激活函数；Wki、θj—隐含层到输出层的权值和输出层的阈值。(k=1，2，3…，L)；g2—输出层的激活函数—输出层第k个神经元在样本p作用下的输出。对于每一个样本P的输入模式对的二次型误差函数为：

BP网络的实质就是根据误差Jp函数梯度变换的反方向不断的调整网络的权值和阈值，当网络的全局误差或迭代次数满足设定的条件时，网络停止训练。

训练数据的准备工作是网络设计与训练的基础，数据选择的科学合理性不但影响网络的学习和泛化能力，而且影响网络的精度。

因前三个关节角度由解析法求出，所以训练样本只针对后三个关节角取值，假定选取各个关节角度的间隔为θ，单位为度，可得总的样本容量N为：

选取训练样本时，若取各关节的角度间隔θ=2时，可得N=757666。虽然样本覆盖范围较广，但样本之间可能存在冗余和矛盾样本，因此要对样本进行优选。

许多学者完成了用模糊C均值聚类算法（FCM）对样本数据进行聚类，但该算法存在的严重缺陷是对初始聚类中心敏感且不易收敛于全局最优，因此，这里采用基于核的改进的模糊C均值聚类算法（KFCM）[9-10]对训练样本进行优选。它通过核函数将训练样本映射到特征空间中，求取聚类中心，使得目标函数最小，目标函数为：

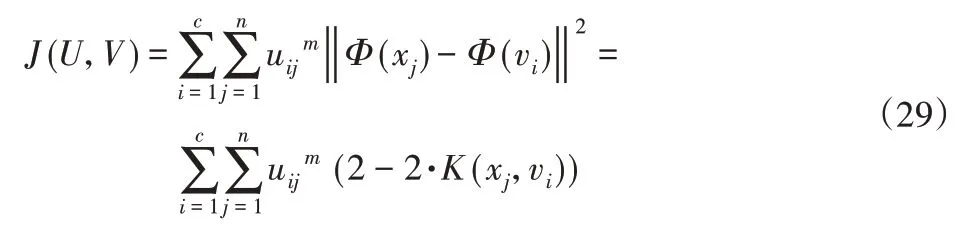
式中：K(xj，vi)—高斯径向基函数。得：

利用拉格朗日的极值必要条件，得出：

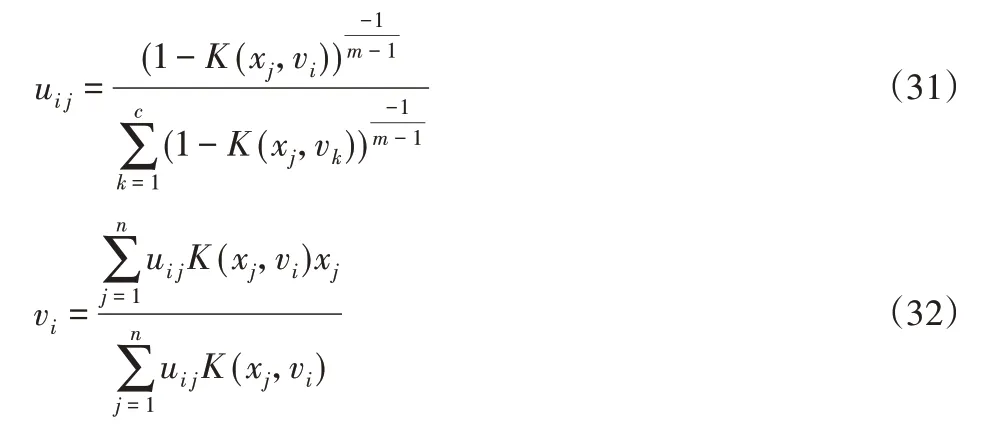
式中：uij—第j个样本属于第i个聚类中心的隶属度；

vi—第i个聚类中心；

m—模糊指数；

δ—径向基函数的参数；

c—聚类个数；

采用上式可得到训练样本数据的聚类中心，接下来用随机抽取算法优选训练样本。算法步骤如下；

（1）确定各个关节角度取值间隔，通过机器人正运动学得出机器人手抓末端工具相对于第三个关节的位姿矩阵样本数据。

（2）对样本数据进行预处理，剔除矛盾样本和冗余的样本，以减少样本容量。

（3）设迭代次数k=0，算法最大迭代次数为maxiter，收敛精度ε，用FCM算法初始化中心矩阵V(0)。

（4）用式（31）、式（32）计算Uk+1，Vk+1，令k=k+1。

（5）重复步骤④，直到满足如下终止条件；k≥maxiter或或存在i(1 ≤i≤c)使得。

（6）采用随机抽取算法对聚类后的样本进行选取，得到优选的网络训练样本。

由于网络的输入数据常常具有不同的物理意义和量纲，为防止因净输入的绝对值过大而使神经元输出饱和，需对训练样本进行归一化处理，归一化后的样本参数范围在(0，1)，归一化的公式为：

式中：xi-输入/输出数据；xmin-数据范围的最小值；xmax-数据范围的最大值。

根据以上算法步骤，在机器人的工作空间范围内约选出2000个训练样本，对手抓末端位姿经式（16）变换，然后经式（33）进行归一化处理，参考文献［11］中方法，对BP神经网络进行训练。

经过训练后的关节角度是（0～1）之间的数，需要进行反归一化处理，即：

4 6R机器人轨迹仿真

4.1 运动轨迹

为了验证该逆解模型方法的正确性，根据该6R模块化机器人的结构参数，用Matlab软件的Robotics工具箱建立机器人连杆模型，并使机器人手抓末端仿真一段圆弧曲线，如图3所示。

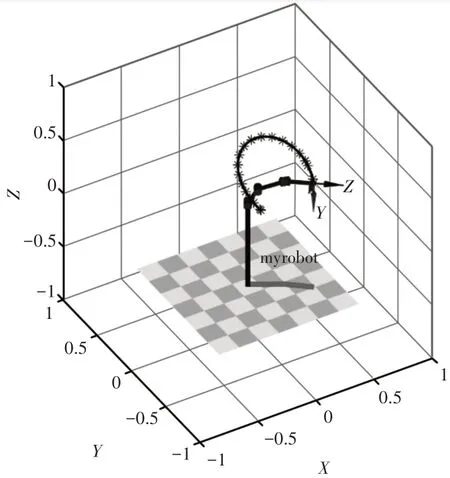
图3 机器人作业轨迹图Fig.3 Robot Operation Trajectory Diagram

随机取20个点作为预测点，并确立这些点的末端姿态，由式（15）、式（16）得到20组α、β、γ、Px、Py和Pz，经归一化后作为BP神经网络的测试数据，得到20组网络预测输出值，并由式（34）反归一化处理。

4.2 逆解模型效果评定

为了验证该逆解模型方法的有效性，采用以下两个指标绝对误差和均方根误差进行评价，即：

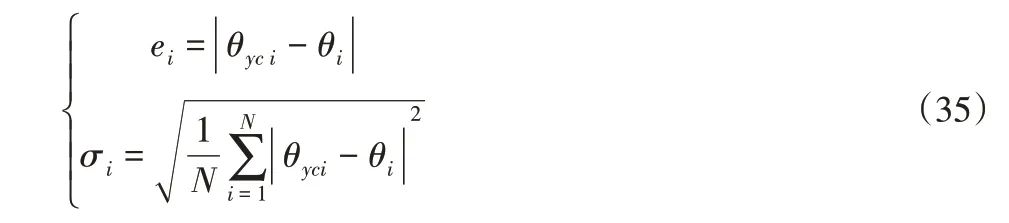
式中：θyci—第i个关节的逆解角度；θi—第i个关节角度的理论值；N—测试样本数，N=20。

由于采用解析解+BP神经网络求逆解，逆解存在多解，为了更好评定网络预测的效果，逆解只选取与20个位置点关节角的理论值相对应的角度。20个作业位置的关节角度理论值、逆运动学求解值、关节角预测误差值，如表2所示。求得后三个关节角在20个作业位置的绝对误差值，如图4所示。

表2 6R机器人20个作业位置的逆解Tab.2 Inverse Solution of 20 Working Positions of 6R Robot

图4 后三个关节角绝对误差值Fig.4 Absolute Error of the Angle of the Last Three Joints

从表2和图4中看出，前三个关节角的绝对误差和均方根误差均为0，证明了该正运动学模型建立和解析法求解的正确性。后三个关节角求解的绝对误差最小值为6.8212e-8，绝对误差最大值为2.0922e-4，均方根误差最小值为1.1812e-5，均方根误差最大值为1.2218e-4。通过以上数据可以看出，基于前三个关节解析法+BP神经网络的逆解预测模型具有很高的求解精度。

为了客观的评价该算法的求解精度和可行性，用和该算法类似的求解步骤分别建立不同组合的数学模型(qmax=3)；0 解析+BP、1解析+BP、2解析+BP。

根据表1中6R机器人关节转角限制范围任取两组关节角，对以上建立的不同组合模型进行逆解求解精度的对比，结果，如表3所示。

通过表3 对任取两组关节角逆解求解的结果得出，0解析+BP求解的绝对误差最小值为0.0474，绝对误差最大值为0.2972，均方根误差为0.1623，1 解析+BP 求解的绝对误差最小值为0.0000，绝对误差最大值为0.1344，均方根误差为0.0653，2解析+BP求解的绝对误差最小值为0.0000，绝对误差最大值为0.0928，均方根误差为0.0402，3 解析+BP 求解的绝对误差最小值为0.0000，绝对误差最大值为0.0001，均方根误差为6.4550e-05。通过对比以上数据的绝对误差值、均方根误差值，3解析+BP组合模式的误差均小于其它的求解组合模式，说明该求逆解组合方式不但模型更优、计算周期短，而且具有较高的求解精度、泛化能力和鲁棒性。

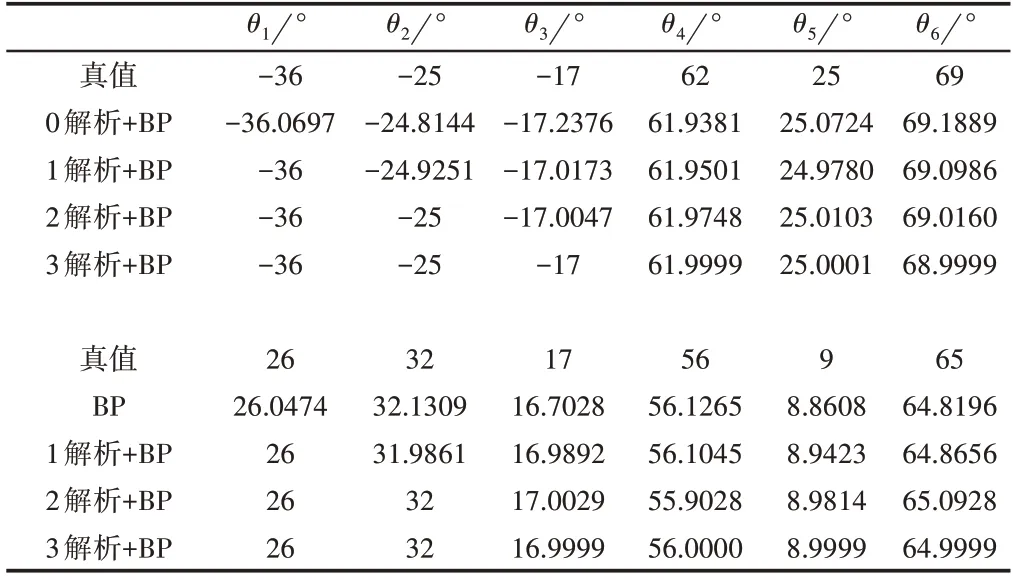
表3 6R模块化机器人不同组合模式的逆解Tab.3 Inverse Solution of Different Combination Modes of 6R Modular Robot

5 结论

（1）提出了一种解析法+BP神经网络相结合求解6R机器人逆运动学的方法，并以6R模块化机器人为例进行逆运动求取，通过运动学轨迹仿真验证了该方法的有效性与可行性。

（2）通过对q解析法+BP神经网络相结合求逆解的4种组合模式进行仿真误差精度对比，结果显示随着q值的增大逆解模型的求解精度逐渐提高，且进行神经网络训练时矛盾样本的容量逐渐减少，缩短了样本筛选的时间周期，即当q=3时，该逆解模型最优。

（3）3解析法+BR神经网络建立的求逆解模型可广泛用于其他一般的6R机器人，获得较高的逆解精度、较短的计算时间周期并能准确的进行轨迹规划。