最优共振频带提取的高速列车轴承故障诊断

刘玉婷，林建辉，李艳萍，赵值正

（1.西南交通大学牵引动力国家重点实验室，四川 成都 610031；2.四川省冶金设计研究院，四川 成都 610081）

1 引言

滚动轴承作为各种机械设备的关键部件，在高速列车上得到了广泛的应用，但轴承易发生故障，引起工程事故，因此对轴承故障的准确识别至关重要。

当滚动轴承存在元件局部缺陷时，该故障区域与元件其它工作表面接触，在轴承运行过程中产生冲击。

由于故障冲击信号振动强度及频域覆盖范围较大，可能激发轴承、轴承座等振动系统的固有频率[1]，因此，为了实现轴承的故障识别，识别并提取振动加速度数据中的故障冲击信号，常采用共振解调技术，计算最佳共振频带内的信号包络谱。峭度可作为信号冲击脉冲度量指标[2]，有效识别共振频带；在此基础上，文献[3]提出了新的指标谱峭度（Spectral Kurtosis,SK），文献[4-5]分别提出了基于短时傅里叶变换与基于有限脉冲响应（FIR）滤波器组的谱峭度计算算法，后者大幅减少了谱峭度的计算时间，并提出了快速峭度图（Fast Kurtogram），极大地拓展了谱峭度的应用范围。

文献[6]提出了基于包络谱峭度的频带选择方法，并在飞机发动机振动信号中得到了有效的应用。但在实际工程中，由于采集的振动信号信噪比较低，并存在周期脉冲干扰，准确检测共振带仍然是轴承诊断中的挑战性问题。针对以上方法的不足，文献[7]在2016年提出了新的故障信息评判指标HSI，即谐波有效指数，并将其应用于轴承故障信号的共振频带识别。

该方法有效地利用了轴承的先验知识，提出了改进的谐波乘积谱（IHPS），寻找振动信号中引起故障冲击的调制源。在文献[7]的基础上，这里对谐波有效指数进行了改进，建立了新的评判指标，并结合完整的频域分割框架得到最优振动频带；引入经验小波变换（EWT）建立滤波器，进行最佳共振频带的提取，最后对通过滤波器后的分量信号进行Hilbert变换，解调得到轴承的故障特征频率。通过仿真与实验数据验证，该方法在一定程度上降低了噪声的干扰，精确提取出轴承故障特征频率及其谐波成分，实现轴承的故障诊断。

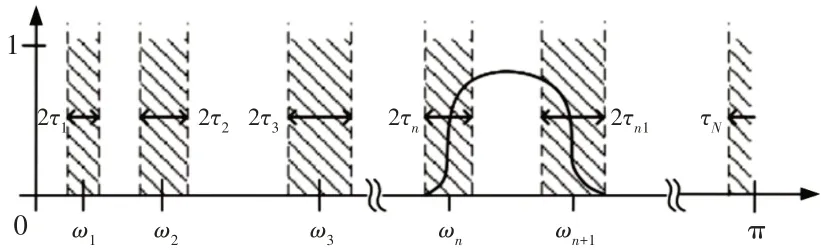
图1 Fourier谱分割图Fig.1 Fourier Spectrum Segmentation Diagram

2 理论基础

2.1 经验小波理论

首先对故障信号进行FFT分析，根据Shannon准则的要求，在分析过程中把信号的Fourier频谱定义在[ 0,π ]范围。

构造经验小波的方法与传统小波变换相同，细节系数与近似系数可由下式得到：

2.2 故障特征指标HSI

轴承故障产生的冲击信号可用幅度调制信号进行表示，其包络谱由轴承故障频率分量及多次谐波组成。考虑到轴承故障信号的包络谱特性，文献[7]引入了语音信号中谐波频谱结构识别[8-9]的谐波谱（Harmonic Product Spectrum，HPS），改进后将其应用于轴承故障识别。语音信号的谐波谱定义如下：

式中：F(w)—信号包络谱在频率w处的取值；K-计算的谐波最大次数。在这里，取K=3。

在此基础上，文献[7]进一步提出了谐波显着性指标以量化诊断结果，减少了信号噪声及计算次数K对计算结果的影响，通过归一化建立了故障指标的物理意义。

无量纲的谐波谱定义如下：

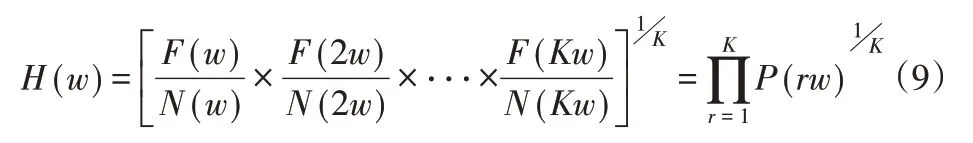
式中：N(w)—频率w附近的信号噪声，可由移动平均滤波器进行计算；P(rw)—频率w附近信号与噪声的幅值之比，反映了频率w处信号显著性。

为了对列车轴承的故障程度进行判断，将轴承的外圈、内圈及滚动体等故障频率wf代入式（9）进行计算[10]，可得到故障特征指标HS（IHarmonics Significance Index）。在列车实际运行中，考虑到转速波动及轴承滑动的影响，轴承实际故障频率与计算理论值存在差异，这里取频率波动值Δw=3Hz，实际故障频率波动范围为[wf-Δw，wf+Δw]进行计算。

2.3 频域分割框架

根据轴承的振动机理，故障信号频谱存在形成以共振频率为中心频率，故障频率为间隔的边频带。

为了得到最优共振频带，文献[10]基于粒子群最优算法对中心频率与频率带宽进行了计算，但计算时间较长；文献[6]根据边频带宽度，首先确定了带宽，再通过包络谱峭度值大小对最佳中心频率进行寻找；文献[11]考虑到轴承外圈、内圈、滚动体及保持架故障频率与轴承转速的计算关系，建立了频率带宽与轴承转速之间的倍数关系，具有一定的自适应性。

考虑到计算的谐波最大次数K=3，fBPFI为轴承内圈故障频率，定义频带宽度为：

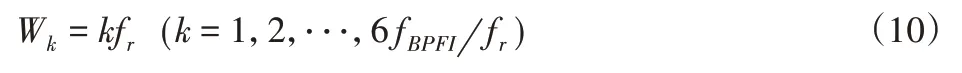
对应的中心频率Fk为：

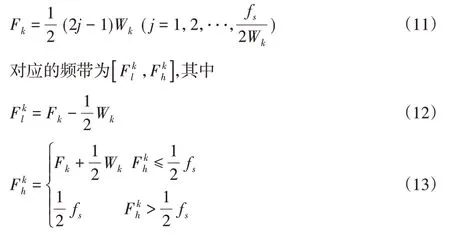
3 最优共振频带提取

计算频带过窄时，频带包含的故障谐波少，对应的包络谱故障频率幅值能量低[6]，难以与噪声区分；计算频带过宽时，提取的频带与原始频谱差异较小，在噪声的影响下，特征频率难以凸显。因此，将频带宽度作为频带包含故障信息的影响参数，对故障特征指标HSI进行改进，得到新的判断指标HSIB，其定义，如式（14）所示。

因此，故障信号最优共振频带提取的具体步骤为：

（1）计算轴承故障频率，根据频域分割框架得到不同宽度的频带；

（2）计算各带宽下频带的故障指标HSIB；

（3）取各中心频率处HSIB的最大值作为该频率点的故障特征值，通过三次样条插值得到HSIB在频域的分布趋势；

（4）计算HSIB的极大值，以该点对应的频率与带宽作为最优共振频带；

（5）通过经验小波变换提取频带，计算信号分量包络谱。

基于最优共振频带提取的高速列车轴承故障诊断流程，如图2所示。

4 仿真验证

为了验证提出的最优频带提取方法的有效性，建立了轴承外圈故障模型进行验证。

考列车轴承实际运行中，受到随机噪声及周期谐波的影响，提出的信号模型，如式（15）所示。

式中：s1(t)—轴承外环故障信号，故障频率fBPFO=161.5Hz；A—故障冲击幅值，A=0.5；fn—系统共振频率，fn=2500；β-冲击衰减系数，β=1000；T—冲击时间间隔，T=1/fBPFO；u(t)-单位阶跃函数，冲击次数N=1000；s2(t)—周期谐波干扰；fr=20Hz；n(t)—高斯白噪声，信噪比为0dB。设置采样频率为10000Hz。

仿真信号s(t)的时域波形，如图3所示。

图3 仿真信号时域波形Fig.3 Time Domain Waveform of the Simulated Signal

计算各频带故障特征值，得到HSIB在频域的分布趋势，如图4所示。

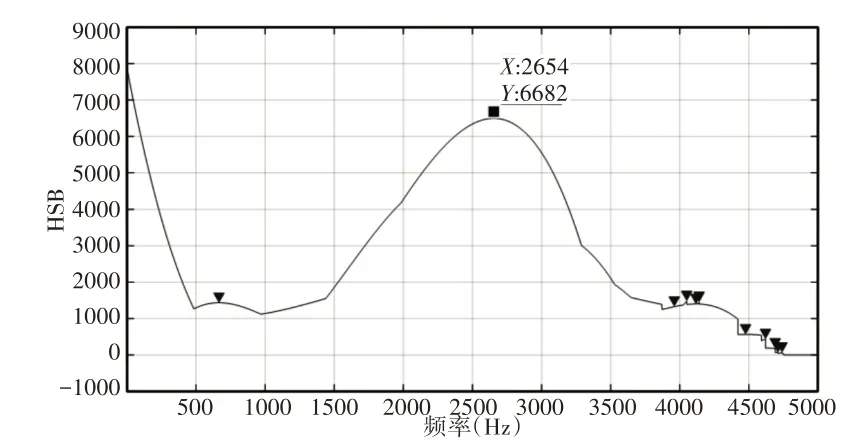
图4 仿真信号HSIB分布趋势Fig.4 HSIB Distribution Trend of the Simulated Signal

可得HSIB 峰值处频率值为2654Hz，频带宽度为980Hz，对应的共振频带为［2164Hz，3144Hz］，如图5所示。

图5 仿真信号最佳共振频带Fig.5 Optimal Resonant Frequency Band of the Simulated Signal

虚线包含的频率即为计算得到的最佳共振频带。通过经验小波变换中的滤波器组对判别的最佳共振频带进行提取，可得信号分量的时域波形，如图6所示。

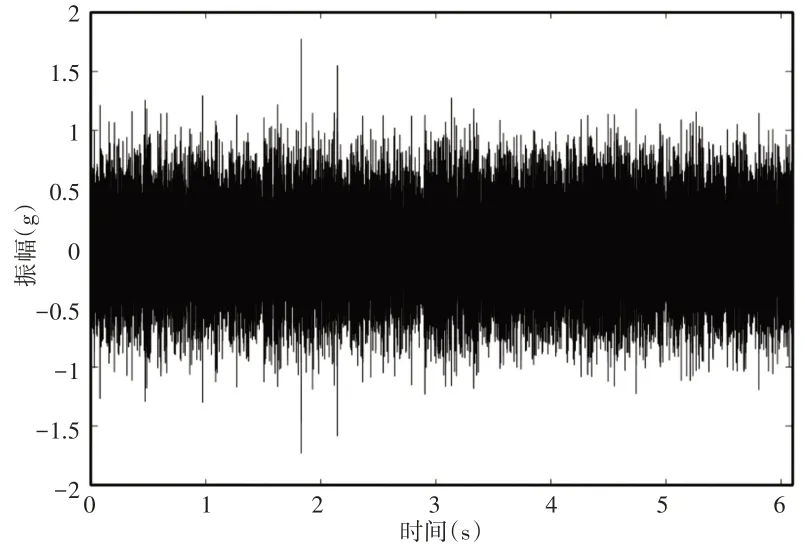
图6 仿真信号故障频带时域波形Fig.6 Time Domain Waveform of the Fault Band

对提取的信号分量做Hilbert变换，得到包络谱，如图7所示。仅显示了（0～1000）Hz的频率信息。

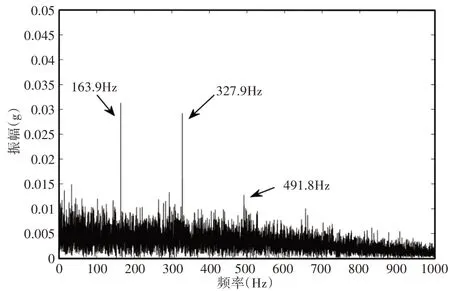
图7 仿真信号故障频带包络谱Fig.7 Fault Band Envelope Spectrum of the Simulated Signal

根据已知的轴承仿真信号外环故障频率，可以得到故障频率及其二次、三次谐波，实现轴承故障的准确判断。

5 实验验证

5.1 实验数据获取

利用实际工程信号来验证算法的有效性，测试对象为CRH380A齿轮箱输入轴圆锥滚子轴承，被测试轴承的部分参数，如表1所示。信号采样频率为10000Hz，采样周期20s，主轴的转速为3195 r/min，轴承的回转频率为f=53.25Hz。

表1 CRH380A齿轮箱输入轴圆锥滚子轴承基本参数Tab.1 Basic Parameters of CRH380A Gearbox Input Shaft Tapered Roller Bearings

轴承外圈故障频率fo可由式（16）计算得到。

结合式（15）和表1，可计算出轴承外圈故障频率为271.3Hz。

5.2 轴承外圈实验数据验证

故障信号时域图，如图8所示。由图中可以看出，轴承外圈发生故障时，轴承振动的幅值、波动性非常大，很难分析故障中包含的成分。根据算法计算得到各频带的特征值HSIB 的分布趋势，如图9所示。选取极大值点x=4100处的中心频率与带宽作为最佳共振频带，其在频域上的分布，如图10所示。

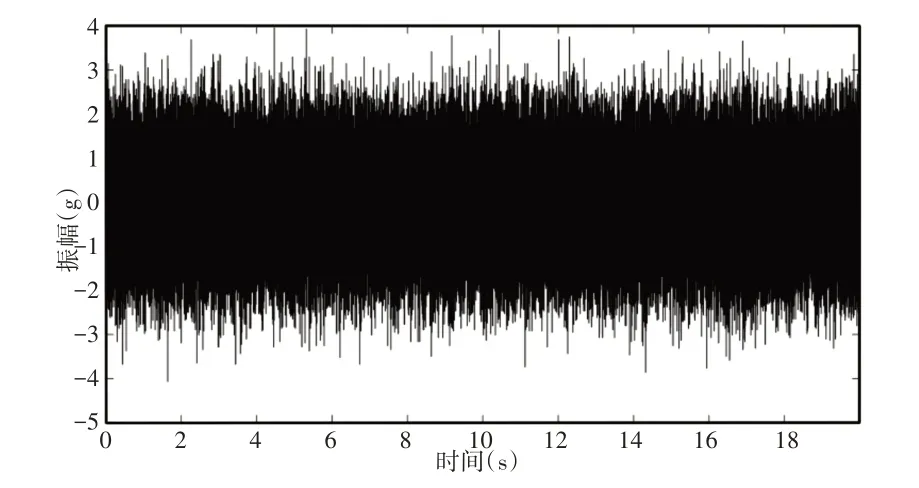
图8 故障信号时域波形Fig.8 Time Domain Waveform of the Fault Signal

图9 故障信号HSIB分布趋势Fig.9 HSIB Distribution Trend of the Fault Signal

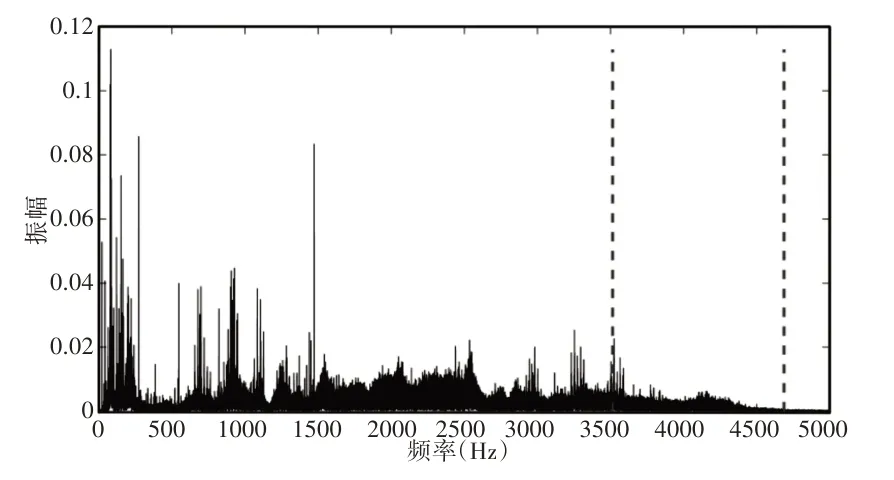
图10 故障信号最佳共振频带Fig.10 Optimal Resonant Frequency Band of the Fault Signal

将频带对应的分量信号通过滤波器组，可得时域波形，如图11 所示。解调后信号分量的频谱，如图12 所示。仅显示了（0～1000）Hz的频率信息。由图可得分量中外圈故障频率较为明显，且包含了故障频率的二倍频，可以判断该轴承具有外圈故障。对齿轮箱进行拆解，齿轮箱轴承外圈存在明显磨损，实际故障情况与判断结果相符。

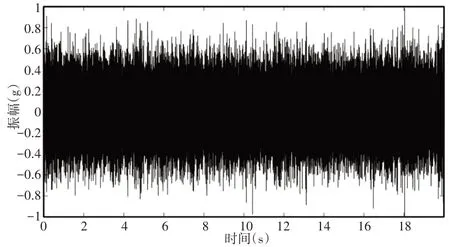
图11 故障信号故障频带时域波形Fig.11 Time Domain Waveform of the Fault Band

图12 故障信号故障频带包络谱Fig.12 Fault Band Envelope Spectrum of the Fault Signal

为了进一步说明提出的共振频带识别方法的优越性，将故障信号通过传统的快速峭度图方法进行分析，得到快速峭度图，如图13所示。

图13 故障信号快速峭度图Fig.13 Fast Kurtogram of the Fault Signal

预设分解层数N=4，该方法识别的最佳共振频带为［0，833.33Hz］，由先验知识可得，轴承振动系统固有频率较高，轴承故障引起的共振中心频率通常大于2000Hz，该判定频带与动力学知识不符。将判定的频带信号通过生成的EWT滤波器组，解调得到信号的包络谱，如图14所示。由图可得，轴承外圈故障频率幅值不明显，仅从频谱频率特征无法得到故障信息，难以实现设备故障诊断。与传统的峭度图方法相比，改进后的方法能够更好的反映频带的故障信息容量，对共振频带进行准确的识别，从而实现故障信息的有效提取。

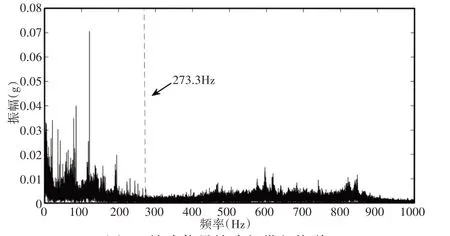
图14 故障信号故障频带包络谱Fig.14 Fault Band Envelope Spectrum of the Fault Signal

6 总结

针对基于峭度的传统共振频带提取方法在噪声干扰下的缺陷，这里提出了一种改进的最佳频带提取方法，并通过仿真信号与实验数据验证了该方法的有效性与优越性。

与传统的共振频带识别方法相比，该方法基于滚动轴承的先验知识，提出了新的故障信息判定指标HSIB。HSIB将轴承故障信号频谱的分布特征转换为可以进行比较的特征值，对噪声以及周期脉冲干扰均有较好的稳定性。与传统的共振解调方法相比，该方法引入了经验小波变换中的滤波器组，对提取的频带信号进行带通滤波。实验结果说明，故障信号在被强烈的非高斯噪声和背景严重污染时，提出的方法也可以识别信号的最敏感频段，并产生明显的故障频率分量及其倍频分量，实现准确的故障诊断。