擦玻璃机器人的自适应阻抗控制研究

尹恒健，倪受东

（南京工业大学机械与动力工程学院，江苏 南京 211800）

1 引言

随着社会的不断发展，高楼建筑越来越多，玻璃幕墙因采光好、美观的特点被广泛的使用，同时清洗高空玻璃的工作变得复杂。一般情况下，清洗高空玻璃的工作有两种方式：人工清洗和升降机清洗。人工清洗会带来一定的危险性[1]，升降机清洗成本较高以及容易出现清洗的死角。为了解决这些顾虑，有些学者也在研究。例如最近几年，文献[2]提出的“基于涵道推力式擦玻璃机器人”的研究，虽然在自由行走时可以克服摩擦，保证机器人不会滑落，但此类擦玻璃机器人结构复杂且成本较高；文献[3]提出的“一种轮足组合式擦玻璃机器人”，大大提高清洗的稳定性，缺点就是自带的水箱重量大，无法实现长时间的清洗。综上，难以解决的两大问题就是清洗时机器人末端的作业位置以及输出的末端接触力是否被外力所干扰。

早在1985年，文献[4]提出的“阻抗控制”这一概念，将位置和力纳入一个动态框架，从补偿性的角度解决了机器人在运动时易受外界干扰的问题，但由于对机器人模型的精确度要求极高，在作业中很难达到预期的效果。后来Seul提出的“自适应阻抗控制”，是在Hogan研究的基础上，增加了延时模块，拥有了较好的鲁棒性[5]。最近几年，自适应阻抗算法多运用于医疗领域，例如基于下肢康复机器人、上肢辅助外骨骼机器人、可穿戴机器人等等，这些机器人的产生，一定程度上减轻了老人以及在事故中受伤的残疾人士的痛苦[6]。与此同时，随着工业领域的需求不断增多，自适应阻抗控制算法的优越性逐渐显示出来。

本研究提出的擦玻璃机器人是在传统工业机器人的基础上，引用了自适应阻抗算法，在机器人处于未知环境时，对机器人末端的位置和力进行一定的规划，减小外界的干扰，确保玻璃达到预期的清洁效果。

2 机器人平台搭建

这里研究的擦玻璃机器人模型平台包括PUMA560机器人、末端清洁器、支撑板，如图1所示。末端清洁器主要由小型驱动器、力传感器以及清洁海绵构成；支撑板水平放置，主要是为了减少机器人在工作工程中左右晃动的现象。当机器人末端的位置和接触力达到预期的数值，玻璃的清洗工作就可以正常进行。

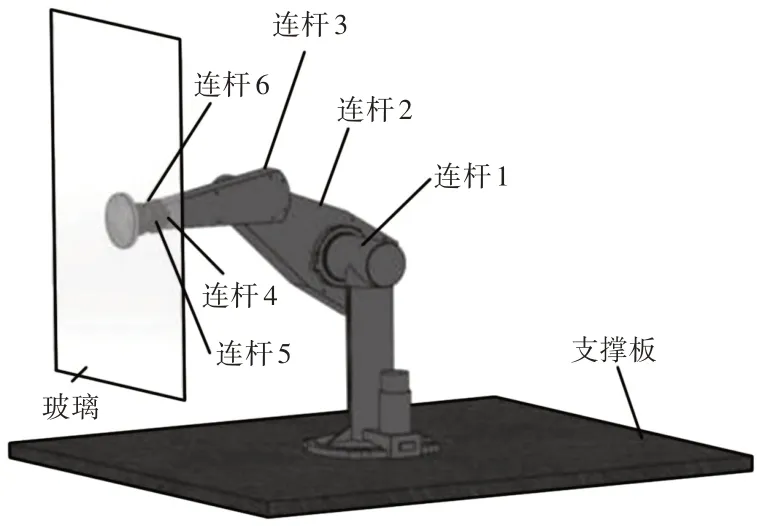
图1 擦玻璃机器人的主要结构Fig.1 Main Structure of the Glass Cleaning Robot

2.1 PUMA560机器人模型的建立

为了完成擦玻璃的任务，选择的理想机器人应具有简便和易于操作的特点，而PUMA560机器人是工业生产中较为常见的机器人，符合这项任务的需求。它有六个转动关节，前面三关节控制了大体的运动方向，后面三关节确定末端的具体位置，这样可以展开六自由度的作业。如表1所示，在D-H 表中，∂i表示扭转角，ai表示横距，di表示连杆长度，θi表示关节角，利用MATLAB中的robotics 工具箱画出PUMA560 机器人的三维模型，如图2所示。

表1 PUMA560机器人的D-H参数Tab.1 D-H Parameters of PUMA560 Robot

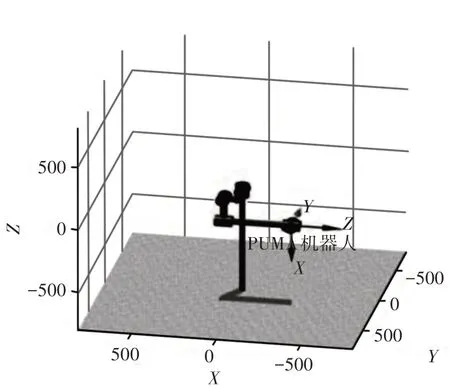
图2 三维空间中的PUMA560机器人Fig.2 PUMA560 Robot in the Three-Dimensional Space

为了便于下面的研究，从输出力矩的角度考虑，取连杆2和连杆3构成两连杆机械臂进行深入的研究，如图3所示。两连杆机械臂的坐标表示，得出末端机械臂的坐标表示为：

图3 两连杆机械臂坐标系Fig.3 Two Link Manipulator Coordinate System

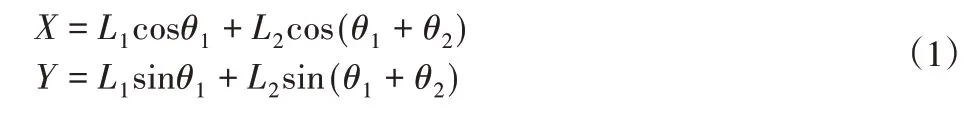
式中：θ1—关节角1；θ2—关节角2；L1和L2—机械臂的长度。

根据雅可比矩阵的定义，末端的坐标值对θ1，θ2分别求偏导，由此推出雅可比矩阵为：

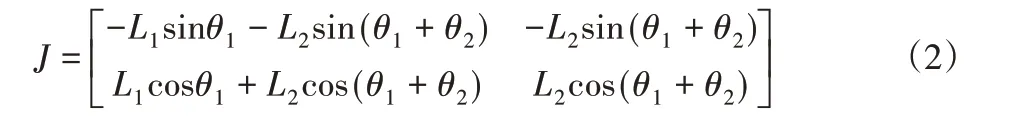
2.2 拉格朗日动力学分析

在工业机器人研究领域，拉格朗日方程为：

式中：L—拉格朗日函数；τi—广义力；θi—变量；—变量的一阶导数。根据前面建立的两连杆机械臂的坐标表示，分别建立整个系统动能和势能的表达式[7]，得出拉格朗日函数：

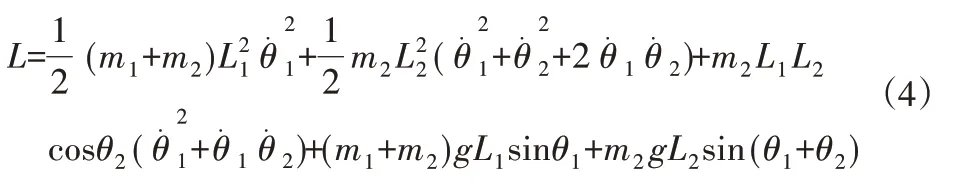
n自由度的机器人动力学方程为：

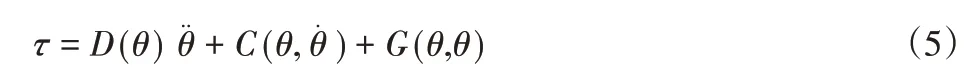
式中：D(θ)—惯性矩阵；C(θ,)—离心力 哥氏力矢量矩阵；G(θ,θ)—重力矢量矩阵。由上面两式结合，得出：

3 自适应阻抗控制器的设计

与传统的阻抗控制算法相比，自适应阻抗控制算法在位置环境下表现出一定的适应性，及时地对力反馈信息进行处理。

更重要的是，自适应阻抗算法不需要对机器人建立精确的模型，在实际的工业生产中表现出良好的鲁棒性，能够把机器人与环境之间的接触力和实际的位置稳定在期望值范围内。

3.1 自适应阻抗算法控制器的原理

在外部环境作用下的n自由度机器人的动力学表达式如下：

在传统阻抗控制的基础上，建立新的阻抗的关系式如下：

式中：Fe—机器人与环境的接触力；Fd—期望力；M，B，K—惯性矩阵、阻尼矩阵、刚度矩阵；E—期望位置Xd和实际位置X之差。

式中：为了后续研究的简便，将参数Fd，Fe，M，B，K对应为fd，fe，m，b，k。

由于在实际的过程当中，自由空间下的状态是不存在的，所以只考虑接触空间这类情况。

仿真中没有传感器，所以将刚度系数设置为零，在力控方向上假设：

式中：ke—环境刚度。

其中，考虑到实际的工作环境，要对环境位置有个大概的估计值Xe，设e′=e+δXe。

为了保证力误差的稳定性，自适应阻抗方程为：

由式得出，自适应阻抗算法的框架，如图4所示。

图4 自适应阻抗原理框图Fig.4 Adaptive Impedance Schematic Diagram

3.2 自适应阻抗算法的仿真研究

假设两连杆机械臂的两关节长度都为1m，质量都为1kg得出：

故特征值下界ρ为0.172，由于估计矩阵且0 ＜α＜2ρ，所以得出：0 ＜α＜0.344。为了方便后续与粒子群算法优化后的仿真结果作对比，下面仿真只针对X方向上的接触力（允许有0.01的误差），自适应阻抗控制仿真模型，如图5所示。

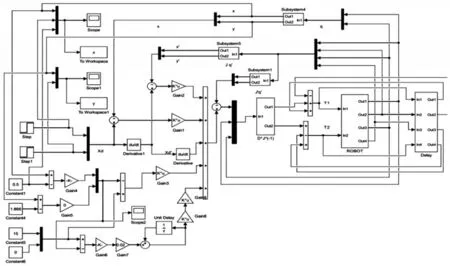
图5 自适应阻抗算法的simulink仿真模型Fig.5 Simulink Simulation Model of Adaptive Impedance Algorithm

仿真模型中，6个S函数分别表示笛卡尔空间内X，Y的坐标、、ROBOT模块（输入总力矩，求出逆解得出角度和角速度）、延时模块，根据图中的原理框图依次搭建好simulink模块。

其中延时模块的内部结构，如图6所示。

图6 延时模块Fig.6 Delay Module

根据图7 所示，在X，Y方向上加入阶跃信号分别为Xd=0.51,Yd=1.866，将期望力控制在15N，环境信号（规划的位置）X=0.5，Y=1.866，仿真模型中三个阻抗参数分别设置为：

图7 机械手的初始位置Fig.7 Initial Position of Manipulator

图8 X方向上的位置Fig.8 Position in the X Direction

图9 X方向上的力Fig.9 Force in the X Direction

由上图可以看出，X方向的位置始终在误差范围之类，最大的实际的接触力达到25.5364N，经过1.618s，接触力稳定在15N。综上分析，采用自适应阻抗算法设计控制器，不仅能有效地实现位置控制，对机械臂末端的接触力有明显的控制效果。

4 粒子群算法优化参数

在这里，采用粒子群算法主要是优化自适应阻抗算法中的M，B，K三个参数，不断的更新粒子的速度和位置，从而使整个自适应阻抗算法达到理想的效果[10]。适应度函数决定粒子的优劣采用的函数如下：

式中：μ1—力误差，表示位置误差；ρ—常数，范围是（0～1）。

4.1 搭建粒子群算法（PSO）自适应阻抗控制平台

Fcn模块力包含适应度函数，u1表示期望位置和实际位置的差，u2表示期望力和实际力的差，p为一个0到1的常数，Out表示适应度值的输出，如图10所示。

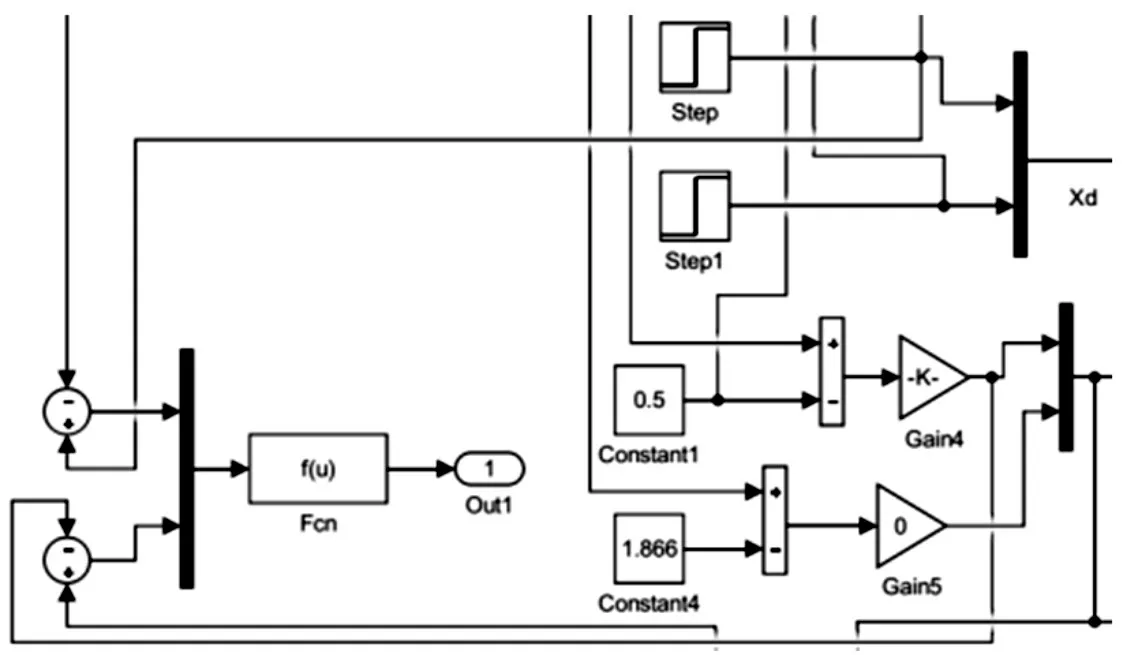
图10 粒子群算法优化的自适应阻抗控制器Fig.10 Particle Swarm Optimization Adaptive Impedance Controller

为了让粒子群算法中的主函数和适应度函数连接起来，需要用到以下脚本语句：

将粒子群算法生成的粒子通过Assignin函数赋值给仿真模型中的M，B，K三个参数，进行离线运算。在算法的主程序中，粒子的维数设置为3，粒子数目为20，迭代次数为100，加速参数都为2，惯性参数为0.6，粒子的速度为[-1，1]，粒子上下限分别为[0，40，500]，[2，100，70]。结果，如图11所示。

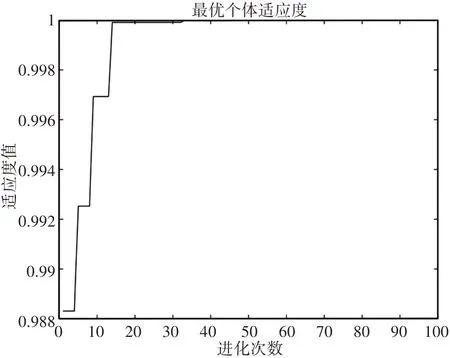
图11 适应度值迭代曲线Fig.11 Fitness Value Iteration Curve

由上图可以看出，迭代次数达到32时，适应度值完全收敛，此时选取的M，B，K的值为最优值，分别为1.0292，87.7710，595.9844。X方向上的力，如图12所示。

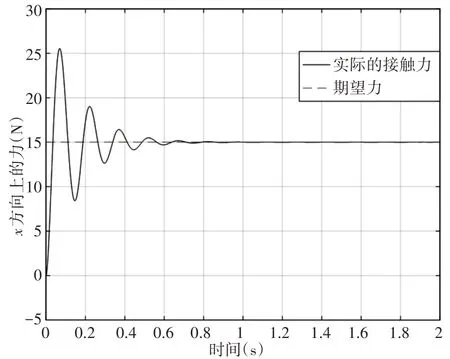
图12 粒子群算法优化后的X方向上的力Fig.12 Particle Swarm Optimization in the X Direction of the Force

和前面的自适应阻抗仿真模型相比（因为两者都能使X方向上的位置稳定在误差之内，故不作讨论），PSO优化后的结果是经过1.163s，接触力稳定在15N，提前了0.455s。这表明经过粒子群优化后的自适应阻抗控制器稳定时间缩短，起到了明显的优化效果。

4.2 测量PSO-自适应阻抗控制器承受的范围

上文中的接触力15N显然不是PSO-自适应阻抗控制器承受的最大极限值，为了进一步研究此控制器，将15N的力慢慢叠加，过程中出现了两个关键的节点数据，分别是23N和500N时候机器人末端的位置和力的控制情况，如图13、图14所示。仿真结果表明，在一步步增大期望力的时候，期望力在（0～23）N时，机器人末端位置和接触力都能被有效的控制；期望力超过500N时，仿真过程中开始报错，即控制器最大承受力为500N，但位置无法被限制误差范围之内，超过理想位置约0.2m。

图13 两种情况下X方向上的力Fig.13 The Force in the X Direction in the Both Cases

图14 两种情况下X方向上的位置Fig.14 The Position in the X Direction in Both Cases

因此，在现实的玻璃清洗过程中，对一些刚度较小且清洁度要求高的玻璃（例如住宅区的装饰玻璃），通过将此控制器的期望力设置在（0～23）N之内，可以起到好的效果；对一些刚度高且工作量大的玻璃（例如玻璃幕墙），可以将此控制器的期望力设置在（23～500）N之内，此控制器都可以满足相应的需求。

5 结论

这里采用自适应阻抗算法研究擦玻璃机器人，在未知的环境下，有效地对机械臂末端的位置和接触力进行控制，在实际的擦玻璃工作中可以有效减少了外界的干扰。

通过引入了粒子群算法，对自适应阻抗参数进行优化。尤其是测量控制器模型承受的最大期望力，在实际生活在中有较大的应用价值。

但研究的过程中仍存在许多不足：针对擦玻璃机器人输出力矩较大的连杆2、3进行研究，对比于6自由度机器人而言，达不到最理想的结果；未立足于实际条件来考虑到关节之间的摩擦因数；没有对粒子群算法进行改进，粒子群易容易陷入局部最优。在今后研究过程中，笔者将重点研究多自由度机器人的研究，立足于实验，对干扰擦玻璃机器人作业的实际因数进行更多的探讨。