求解可分解强凸优化问题的FISTA-Barzilai-Borwein算法
李 星,邓康康, 李 超
(1.福州大学 数学与计算机科学学院,福建 福州 350100;2.武夷学院 数学与计算机学院,福建 武夷山 354300)
近年来,结构凸优化模型及其算法已经成为机器学习研究的热点,尤其是非光滑优化技术。更好地利用非光滑项的结构对于一个算法获得良好的性能是至关重要的。考虑如下形式的可分解强凸优化问题

其中E为欧氏空间。通篇假设:
(a)f:E → (-∞,∞]是强凸函数,dom (f)=Rn,即存在 σ>0,

且在E上梯度▽f是利普希茨连续的,即存在一个常数 Lf,使得
‖ ▽ f(x)-▽ f(y)‖ ≤ Lf‖ x-y‖ ,∀ x,y∈ dom (f);
(b)g:E→(-∞,∞]是闭凸(不一定可微)函数,且dom (g)⊆ int(dom (f));
(c)问题(1)的最优解集Ω*是非空的,最优值记为Fopt。
临近梯度算法[9]是求解各种非光滑优化问题的常用方法之一,具有计算成本低、收敛性强和步长选择广[4,5,6]等优势。该算法具有如下迭代格式:
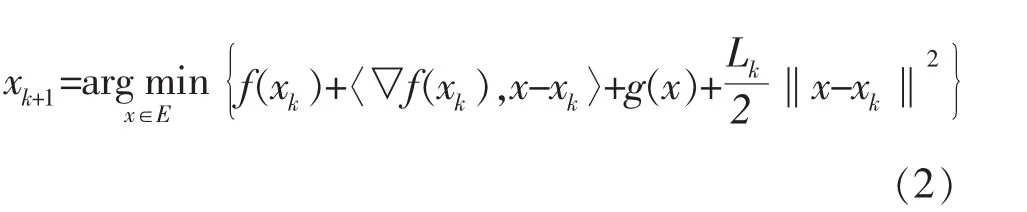
其中▽ f(xk)是 f在 xk处的梯度。
经过简单运算,并省略常数项,可将式(2)改写为
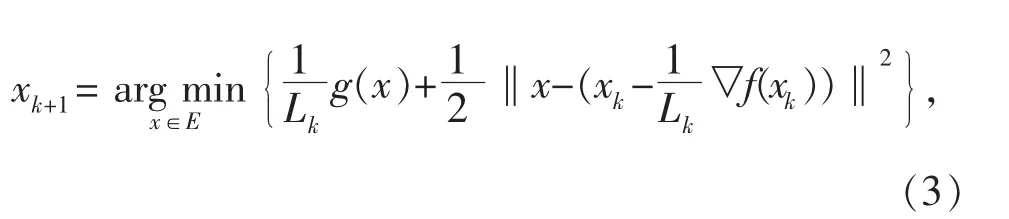
采用临近点算子,式(3)写为
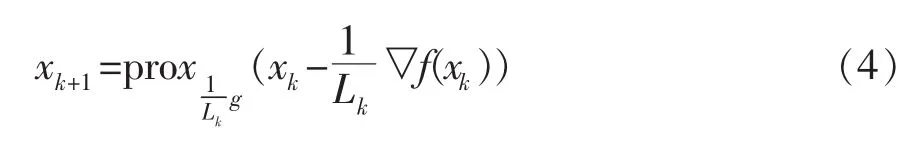
临近梯度算法仅具有O(1/k)的收敛速率,这里k是迭代次数。Beck和Teboulle[2]提出了一种快速临近梯度(简称FISTA)算法,并证明算法的全局收敛性和目标函数值的的收敛速率。虽然FISTA算法[7,8]可以保证目标函数值具有O(1/k2)的收敛速率,但在实际应用中,由于它的局部震荡性,实验效果往往并不理想。为了克服FISTA算法的缺陷,Chambolle和Dossal[3]提出了快速迭代收缩/阈值(简称FISTA-CD)算法,通过对参数更新规则的修正,提高了算法的实现效率,并证明算法仍具有的收敛速率。2017年,Beck[1]总结了大量的一阶优化方法,详细地介绍了不同的可分解优化问题,给出许多有效的求解算法模型,同时证明了算法的全局收敛性和O(1/k2)的收敛速率。
算法1:FISTA-CD算法
初始化:给定 x0∈Rn,t0=1,令
执行下列步骤:

4)令 k=k+1,返回 1);
直到收敛.
Barzilai-Borwein算法[4]是求解大规模无约束优化问题的重要方法之一,该方法在计算当前迭代步长时充分利用前一步的信息,尝试用一个标量矩阵γkI逼近Bk,使Bk=γkI满足拟牛顿公式,达到较好逼近目标函数在xk处的Hessian阵的效果。BB步长具有如下形式

其中 sk=xk-xk-1,yk=▽ f(xk)-▽ f(xk-1)。
受文献[1,3]的启发,提出一种与BB算法相结合的快速临近BB(简称FISTA-BB)算法,主要有两个目的:一是采用BB步长作为FISTA-CD算法中的步长因子,使其有一个好的初始选择;二是选择合适的更新准则,加快算法的收敛速度。
全文结构如下:第1节描述了求解可分解强凸优化问题的FISTA-BB算法,并证明该算法具有全局收敛性和0(1/k2)的收敛速率;第2节通过与当前高效算法进行详细的收敛性能数据比对,从而验证本文所构造的算法的有效性;最后,第3节对全文进行总结。
1 算法描述及收敛性分析
首先定义临近梯度算子

针对问题(1),我们提出一种FISTA-BB算法,具体框架如下:
算法2:FISTA-BB算法
S0)初始化:给定 x0∈Rn,令 y0=x0,kmax>0,ε>0,t0=1,L0>0,ρ∈[0,1],0<q<(2-p)2,μ>1,令 k=0;
S1)计算 xk+1,即
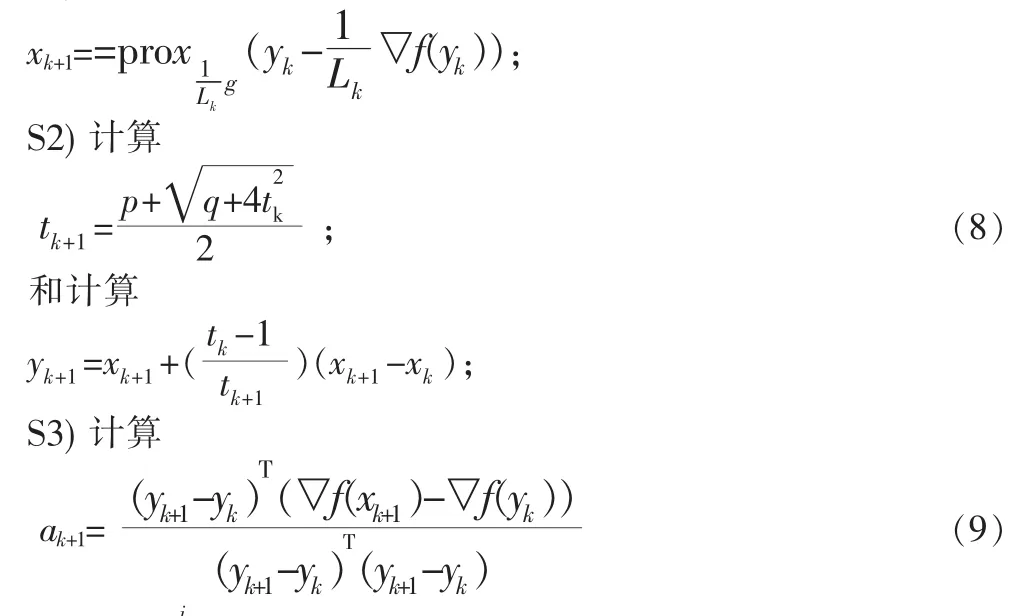
令Lk+1=μkak+1,这里的ik是满足下述条件的最小非负整数,即

S4)当k>kmax或‖ yk+1-yk‖ <ε 时,停止迭代;否则令k=k+1,返回 S1).
为了证明算法的收敛性,先给出如下3个引理:
引理 1:假设 f和 g 满足(a)和(b),对于任意的x∈ E,y∈ int(dom (f)),且 L>0 时,满足
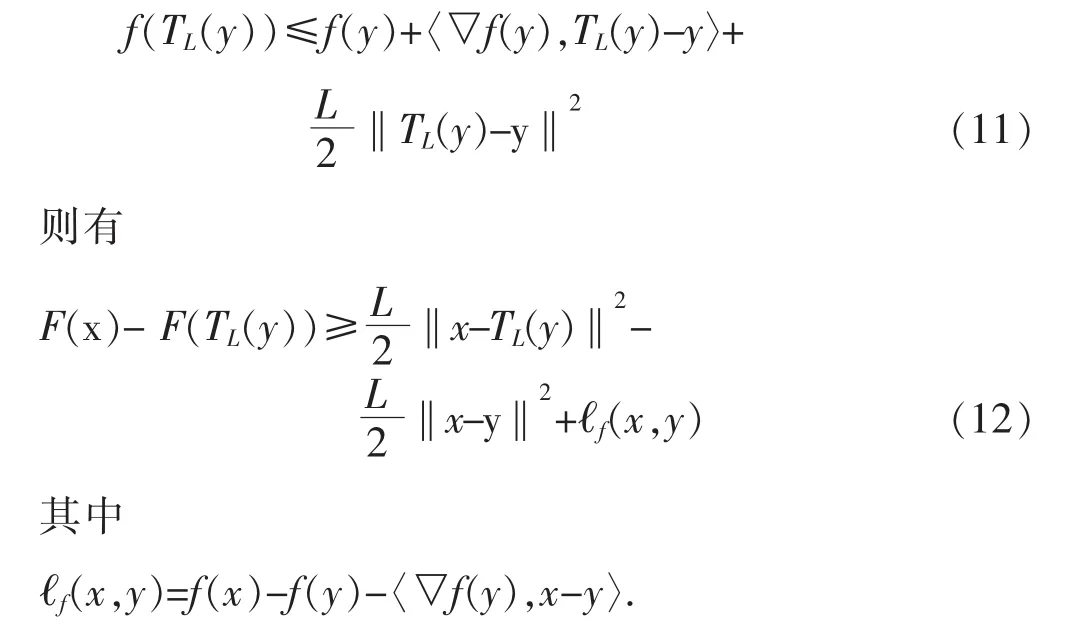
证明:见文献[1]中第281页的定理10.16。
引理 2:假设f是强凸函数,且满足

则对于任意的k≥0,是Lk有界的,即
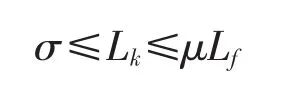
其中 σ>0,μ>1。
证明:由于f是强凸函数,且Lk≥ak>0,则有

从而得到Lk≥σ.
为了证明Lk≤μLf,根据假设中函数f的光滑性,得到
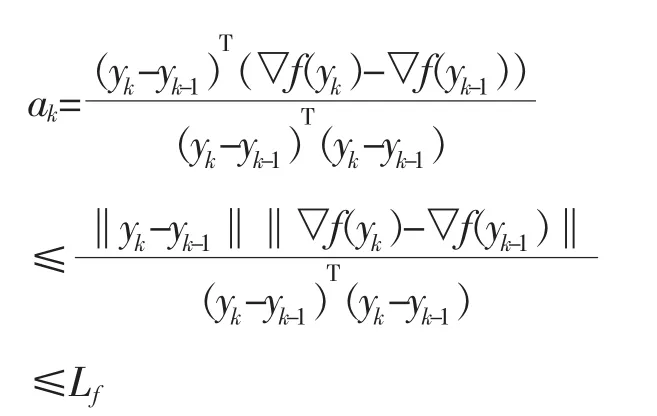
用反证法,假设Lk>μLf,等价于μikak>μLf,于是有μik-1ak>Lf,根据假设中函数f的光滑性有


对式(20),根据 y0=x0,得到

2 数值实验
为了说明算法的有效性,下面对本文所提出的FISTA-BB算法进行初步的数值实验。测试问题均选自文献[1],算法的程序采用Matlab R2016a编制,且所有实验在笔记本为 CPU 1.90GHz,RAM 6.00GB 上运行实现。
算例 3.1[1]:求解如下问题

设计如下实验参数:
终止条件:‖ yk+1-yk‖<ε;
参数设定:ε=1.0e-6,t0=1,L0=2,μ=2,kmax=104,在FISTA-CD算法中取d=2,在FISTA-BB算法中取p=0,q=4;
实验数据:算例 3.1 中,令 λ=0.002,初始点为 x=ones(n,1),x=(1:n/4)=0,b=A*x;算例 3.2 中,初始点为x=zeros(n,1),B=rand(n,n),b=rand(n,1),这里两个算例均取A为对称正定矩阵,定义如下

通过使用MATLAB编程运算得到下面的测试结果,表1和表2均列出了在不同的维数下,分别对算例3.1和算例3.2进行求解,统计FISTA-CD算法和FISTA-BB算法的迭代次数(iter)和运算时间(cput以秒为单位)的结果。

表1 算例3.1的数值结果Table 1 Numerical results of example 3.1
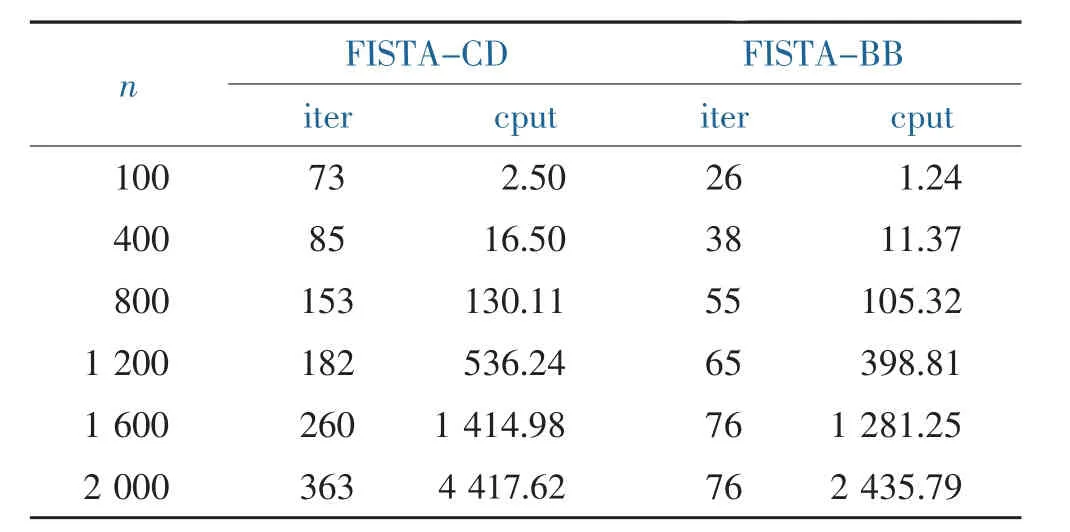
表2 算例3.2的数值结果Table 2 Numerical results of example 3.2
根据上述的数值实验结果可以看出:FISTA-BB算法能够有效求解本文所考虑的相关问题,同时在不同维数的情况下,该算法的迭代次数和运算时间明显优于FISTA-CD算法。
3 结论
本文提出了求解可分解强凸优化问题 (1)的FISTA-BB算法,与文献[3]给出的FISTA-CD算法相比,FISTA-BB算法从很大程度上减少了迭代次数和降低了运算时间.本文证明了FISTA-BB算法具有0(1/k2)的收敛速率,初步数值实验表明了算法的可行性和有效性。

