自然梯度盲源分离加速收敛的衡量依据
陈国钦,陈以勤,詹仁辉
(1.福建技术师范学院电子与机械工程学院,福建 福清 350300;2.福建通信信息报社有限责任公司,福建 福州 350000;3.福建师范大学光电与信息工程学院,福建 福州 350117)
自然梯度算法作为自适应算法中非常重要的方法,由Yang[1]理论上证明了其有效性.算法的稳态误差与步长成正比,收敛时间与步长成反比,因此采用固定步长时,使得收敛速度和稳态误差特性不能同时满足.采用变步长是固定步长不能同时兼顾收敛速度和稳态误差问题的解决方向,即学习率从某一固定步长值开始按倒数递减,但这些应与神经网络输出之间的分离状态相关才具备有效性[2-4].目前盲源分离在许多领域均得到应用[5-10],因此进一步探讨盲源分离加速收敛的有效性问题具有现实意义.
所有信号均有既定的峭度累积量,一个混合信号完成盲源分离时,分离信号的峭度累积量将达到一个既定的累积量,因此峭度累积量是一个与分离状态紧密相关的物理量.该物理量是构造有效变步长自然梯度盲源分离的有效参考物理量[3],同时也是本文探讨自然梯度盲源分离稳定加速方法有效性的观察点.基于该观察点,针对构成自然梯度盲源分离变步长稳定加速方法的有效性衡量问题,结合仿真实验分析探讨一种衡量依据.
首先,观察固定步长自然梯度盲源分离时,在各种不同步长的稳定分离收敛过程,分离信号的峭度累积量随步长迭代的前后之差e(k)遵循一定的变化规律,不同步长的变化曲线相似,只是变化集中范围随步长大小有所不同,并存在一个开始迭代阶段为0的状态,且步长越大该开始段越小;此外,存在一个支持稳定分离收敛的有限步长范围0<η0≤ηmax.其次,再观察明显有效加速方法的变步长盲源分离时,存在以下规则:其一,要保证有稳定分离收敛过程的特征前提是除了变步长应该与分离信号的状态紧密相关,而且分离信号峭度累积量的e(k)也遵循上述相似的变化规律;其二,也存在一个与固定步长自然梯度盲源分离同样的支持稳定分离收敛的有限步长范围0<ηk≤ηmax.
据此得到的结论是,在混合信号的自然梯度盲源分离存在的能保证兼顾分离稳定性和收敛的步长允许范围内,从分离信号的峭度累积量观察,可衡量自然梯度盲源分离稳定收敛提速的因素,存在于分离信号峭度累积量随迭代(固定步长迭代或变步长迭代)变化量e(k)的相似变化特征中,即e(k)变化率为0的开始迭代阶段和变化部分的集中程度两个重要观察指标.因此,当衡量构成与自然梯度盲源分离输出程度紧密关联的稳定加速方法的有效性时,该特征指标就是一个参考依据.
1 固定步长自然梯度盲源分离算法的收敛速度分析
1.1 与分离输出状态相关的峭度累积量
分离信号的峭度累积量是一个与分离状态密切相关的物理量.当输出变量是统计独立的,输出的互信息为0时,分离达到稳定状态,而这时输出的边缘负熵达到最大.假设概率密度函数是对称的,则边缘负熵近似为四阶边缘累积量.四阶边缘累积量k4(i)的归一化计算称作信号的峭度,用于衡量信号偏离高斯的程度.所以可以通过计算分离信号边缘负熵总和代替互信息[3]:
(1)
在盲源分离过程,Jall(k) 是非负的,且从小到大变化,最后达到稳定值(固有的“预设值”).因为不同类型的信号具有不同的固有峭度值,混合信号在达到完全分离时,每个信号将达到其固有的峭度值(实际情形是达到一个很小稳定误差下分离时的峭度值),则各个分离信号峭度的累积量也就达到了稳定值[3].
1.2 峭度累积量反映的固定步长取值范围
自然梯度算法依赖于学习率选择是否得当,如果选择不当而出现稳定性变差,将破坏分离过程的收敛[2-3].以下的仿真实验也验证了这个结果,因此混合信号自然梯度盲源分离中步长存在一个合适取值范围.
实验条件:图1是超高斯的5个语音信号(16 kHz采样率/16 bit,15 000个数据点,通过电脑声卡采集得到的数字信号,φ(yk)= tanh(y)).
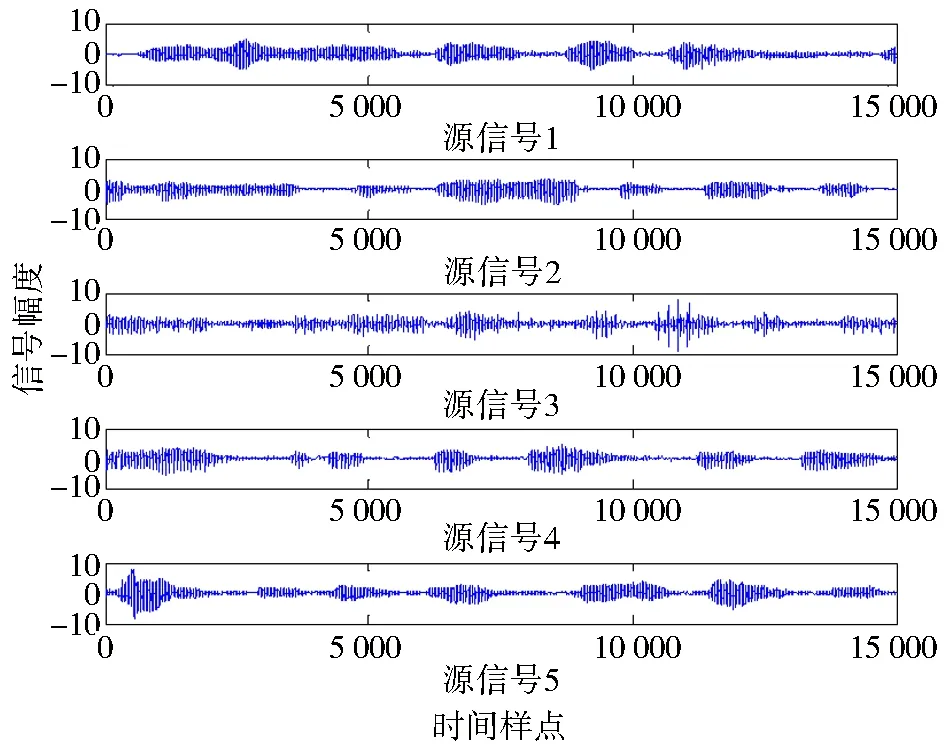
图1 实验的超高斯信号源
实验以随机混合矩阵A对源信号混合.为评价盲分离算法的性能,以“串音”误差为评价指标[3]:
(2)
C是一个置换阵,C=WA,其中cij为C的第i、j个元素,PI表示算法的分离性能,其值越小表示分离的性能越好,当PI=0 时表示信号完全分离.一般情况下,完成分离是达到一个理想的很小值,称为串音误差.
结果分析:图2峭度变化曲线表明,语音混合信号在固定步长大于0.85时就明显地破坏了分离过程的收敛,实际在大于0.8步长时就开始出现不稳定振荡状态.
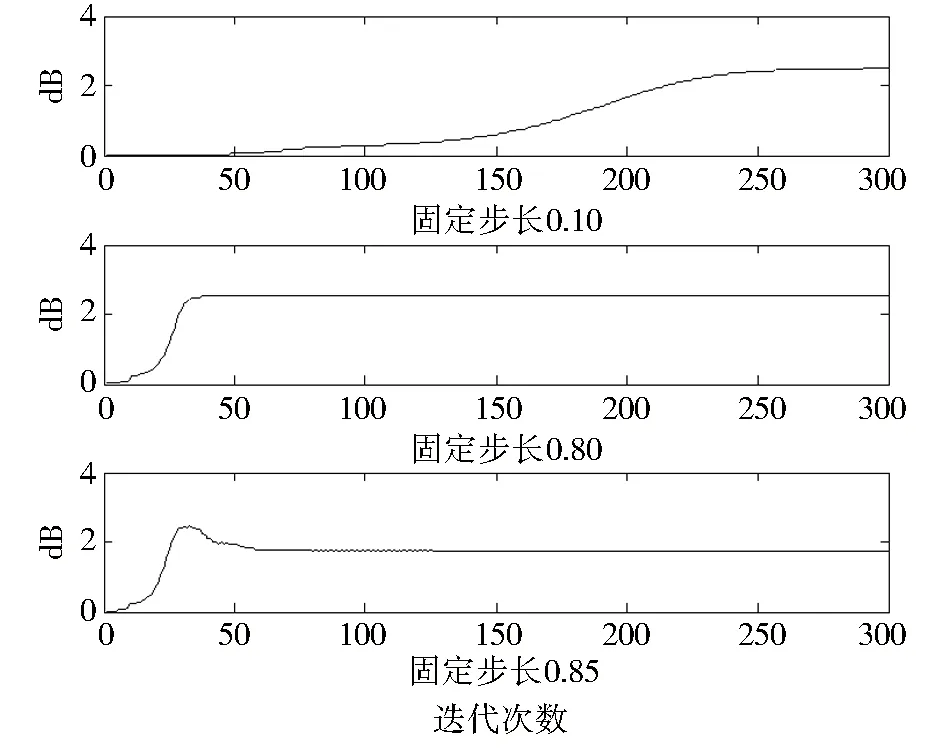
图2 不同固定步长的峭度累积量变化曲线
1.3 峭度累积量反映的稳定收敛变化
若两次迭代之间的取固定步长值η0,则在两次迭代之间,累积量Jall(k) 是从小于1的值不断增大,越接近完成分离而越趋于隐藏的固有“预设值”,最后完成分离.因此,若取两次迭代之间的峭度累积量之差值e(k)来观察,e(k)随迭代的变化状态(以下简称e(k)曲线)将从另一个侧面反映盲源分离的变化规则.变化值e(k)可以用(3)式表示:
e(k)=Jall(k)-Jall(k-1).
(3)
历经N次迭代的过程相当于对e(k) 的积分过程,当累积量等于“预设值”时,分离也达到完成:
(4)
完成分离时的累积量Jall(k)都等于相同的“预设值”.从上述语音混合信号分离过程得到的图2的峭度累积曲线说明,固定步长在允许最大值时都达到最快的分离速度(迭代次数最少),小于最大允许值的步长时,取值越小分离完成得越慢(迭代次数增加).因此,根据(4)式可知e(k)在越少的迭代次数里,将有更大的变化值,即步长越大者,其e(k) 变化斜率和变化值域值越大,反之相反.为了观察e(k) 在取不同固定步长值时的变化趋势,进行以下的仿真实验.
仿真实验:在固定步长0.1、0.4和0.8时,对混合语音信号进行固定步长自然梯度盲源分离实验.峭度累积量Jall(k)两次迭代之间的e(k) 变化曲线分别如图3所示,e(k) 相关变化参数如表1所示.
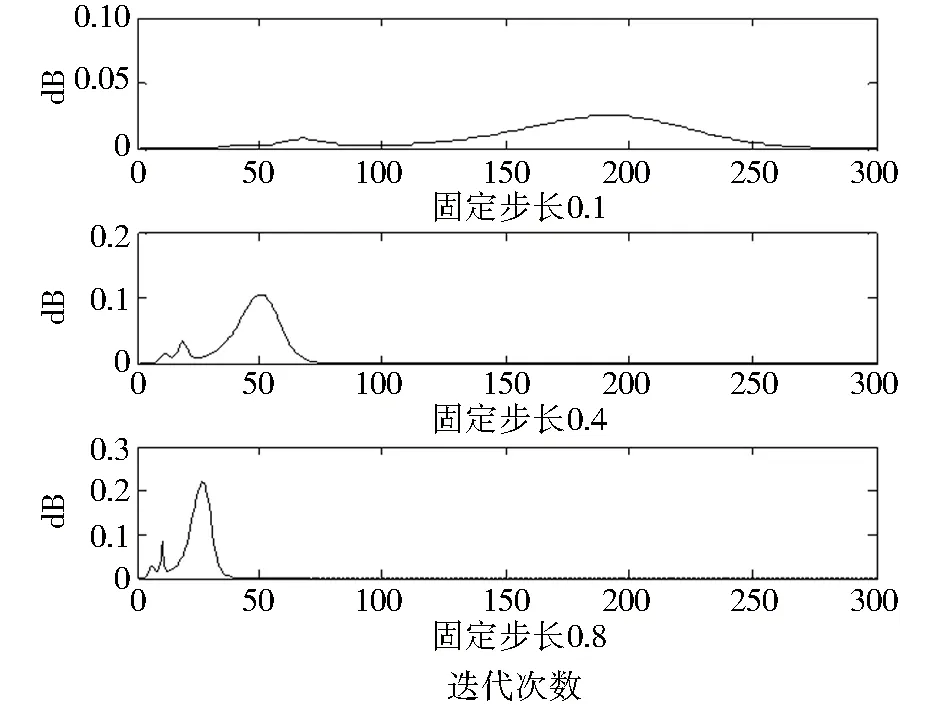
图3 固定步长0.1、0.4和0.8的e(k)变化曲线
结果分析:①从图3可见,几种情况的曲线下面积就是(4)式的结果.以峰值为界,峰值前是峭度累积量的增量变化趋于加速的过程,峰值后阶段是峭度累积量的增量变化趋于减小直至达到“预设值”的过程.步长取值0.1、0.4和0.8的e(k) 曲线是相似的,但步长值越大的e(k)曲线 ,其整个变化将在更短的时间内完成,且e(k) 曲线的值域变化范围和变化斜率(变化速度)也越大.②从表1也可见,步长越小时,迭代计算的分离速度也越低,e(k)曲线的变化值域就越小,尤其在开始阶段,e(k) 曲线几乎无变化率的迭代次数将越多,而此后e(k)曲线明显变化阶段的变化值域和变化斜率也越小,因此根据(4)式完成分离的迭代次数将越多.

表1 固定步长取0.1~0.8时,e(k)等变化参数
综合上述,固定步长自然梯度盲源分离存在以下结论:在混合信号自然梯度盲源分离保证兼顾分离稳定性和正常收敛的允许步长范围内,从e(k) 曲线观察,反映了稳定分离收敛过程,分离过程时间的长短取决于e(k) 曲线无变化率的开始段和集中变化的曲线段.它也是影响收敛速度的两个主要特征.
2 基于峭度累积量微分变步长预测的加速收敛分析
在盲源分离算法中,峭度累积值随分离程度提高而增大,达到完全分离时的稳定值相当于既定的预设值,而分离过程的峭度累积值相当于输出反馈.并且注意到分离信号的峭度累积量是由小到大直至稳定的单向变化过程,而变步长的目的是稳定地加速这个过程.
据此,由于在自动化PID(Proportion Integral Differentiation)算法中,其中利用预设值和输出反馈值间的差值,比例项P是把调节器的输入偏差乘以一个系数,作为调节器的输出;加大比例值可以减少从非稳态到稳态的时间.微分项D是根据差值变化的速率(预测误差的变化趋势),提前给出相应的调节动作.因此,首先,若以初始步长作为比例项,以迭代前后输出的峭度累积量之差相对于步长的变化率作为近似微分项,构成PD(Proportion Differentiation)控制的变步长学习率,则可以在比例作用基础上,给出一个提前预测调节;其次,由于该变步长算法与分离程度紧密相关,则可加快分离收敛速度的基础上又兼顾了稳定性[2-3],图4为基于峭度累积量的PD闭环控制.
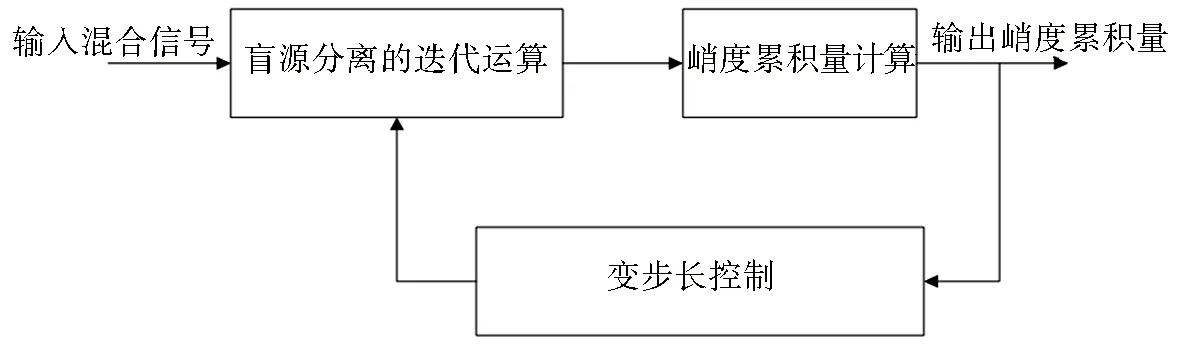
图4 基于峭度累积量的PD闭环控制
下面对该与分离输出程度紧密相关的变步长算法做进一步讨论,说明如何影响上述决定收敛速度的两个特征因素.
2.1 提高微分预测作用因素
因为分离过程是分离信号峭度累积量逐步增大到固有值的过程,因此取与分离过程相关的e(k)变化值相对于步长的比值,近似作为微分预测值,提供相应的变步长增量.利用e(k) 变化值构造预测加速的步长增量:
(5)
显然,随e(k) 变化值将得到合适的步长增量.构造PD变步长学习率:
(6)
为了进一步验证该与分离输出程度紧密相关的变步长盲源分离过程,如何影响上述e(k)曲线两个影响收敛速度的两个特征,根据(6)式采用超高斯信号进行仿真实验.
仿真实验:分别取初始步长为0.1~0.8,在作用系数λ取不同值时,对混合语音信号采用(6)式进行仿真实验,对于不同初始步长取得最大作用系数值时,e(k)曲线相关变化参数如表2所示.其中取初始步长0.1的变步长分离和0.1固定步长分离的峭度累积量的e(k)曲线分别如图5所示.
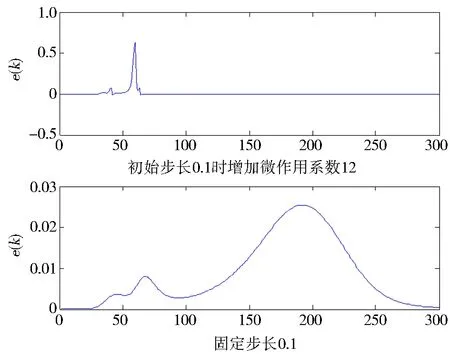
图5 取0.1固定步长和变步长时的e(k)曲线
结果分析:由表2和图5可以看到:分别取初始步长0.1~0.7,并且(6)式作用系数λ取得最大值(无产生不稳定的振荡)时,e(k)曲线具有与上述相似的变化特征,但e(k)曲线开始阶段的变化率现象也保持不变,即迭代次数与表1结果是一样的,只对e(k)曲线出现明显变化率的阶段进一步集中(加速),达到提速效果.最后,当大于0.8初始步长后,开始出现收敛不稳定的状态.
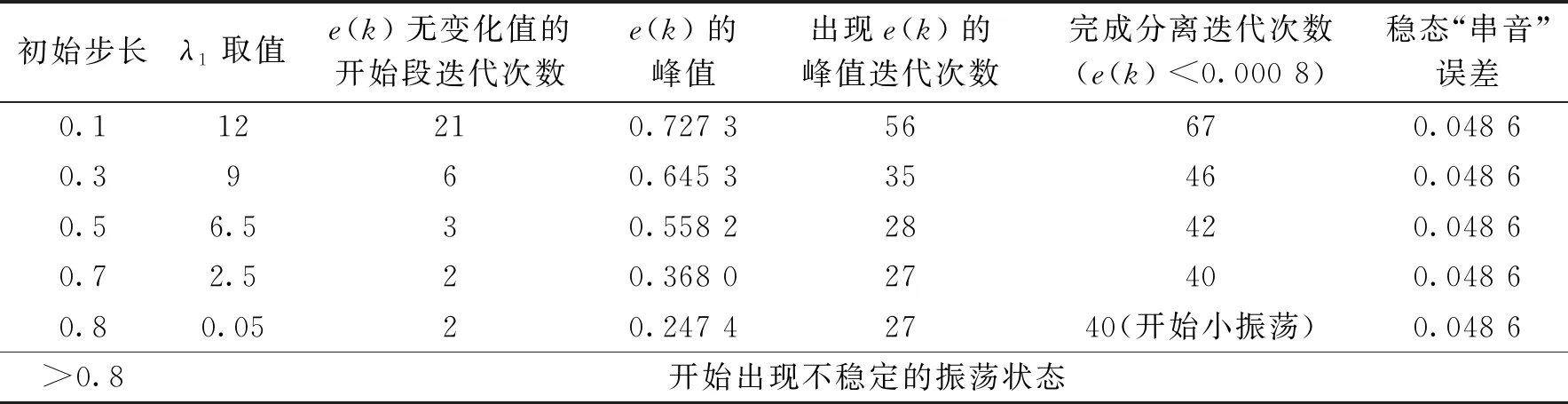
表2 初始步长取0.1~0.8时,(6)式的λ1取得不同最大值时的e(k)等变化参数
综合上述,变步长自然梯度盲源分离存在以下结论:在混合信号自然梯度盲源分离保证兼顾分离稳定性和正常收敛的允许步长范围内,对直接采用(6)式的加速过程, 仅仅影响了e(k) 曲线的变化部分,使变化部分的曲线趋于更集中,由此达到加速效果.而且该实验中微分作用系数取值也达到了可保证稳定分离的上限,因此取各种初始步长下也已经达到加速的上限.
由此说明,若要使整个e(k) 变化曲线往前移动,获得与图5较佳状态相近的e(k)曲线,那么对e(k) 曲线开始阶段的影响是进一步的改造空间.
2.2 改善分离开始阶段的e(k) 变化率
因为注意到分离信号峭度累积量随迭代步长变化的过程,迭代计算前后的e(k)变化值只要有很小的变化,那么e(k)变化值相对于迭代中的峭度累积量Jall(k)也会有较明显变化,并且随着施行加速的开始是个较明显的值,随着收敛过程趋于稳定而趋于0.因此,可以用来改变开始阶段的分离速度,构造新的PD 变步长学习率如下:
g(k)=e(k)/Jall(k),
(7)
(8)
仿真实验:针对混合语音信号源进行两个实验,其一,语音混合信号取固定步长0.1进行自然梯度盲源分离,取得g(k)和e(k)变化曲线如图6所示.其二,语音混合信号在初始步长取0.1以上的值实现(8)式的变步长分离,在取合适(只是一组合适取值,非最佳)的λ1和λ2作用系数时,取得e(k)等变化参数如表3所示;其中由初始步长0.1取得e(k)变化曲线也如图6所示.

表3 初始步长取0.1~0.8时,式(8)的λ1和λ2取不同合适值(非最佳)时的e(k)等变化参数

图6 固定步长0.1分离的e(k)和g(k)曲线;(8)式初始步长0.1分离的e(k)曲线
结果分析:表3结果表明,在混合信号的盲源分离能保证兼顾分离稳定性和收敛的允许步长范围内,采用(8)式进行变步长分离,并在λ1和λ2取合适参数时,e(k)曲线保持上述相似的变化规则.但开始段变化的变化率明显提高了,无变化的开始迭代次数下降到2-3次,整个e(k)曲线前移了,而且e(k)曲线的峰值基本出现在25-33次迭代之间,完成分离的迭代次数(收敛速度)更接近一致的40次左右,均接近较佳的收敛速度.
图6也说明,固定步长分离时,在迭代开始段g(k)一开始就随迭代步长上升到最大的变化率,此后随分离趋于完成逐渐下降,直至完成而降到0.恰如预期,g(k)变化特征与e(k)相反,确实有助于改善e(k) 曲线开始段的状态.
综合上述,(8)式同时有效地影响了e(k)曲线的几乎无变化的开始段和集中变化的阶段,因此整个e(k) 变化曲线前移了,得到更接近固定步长分离时较佳状态的e(k)曲线.此外,当取大于0.8初始步长后开始出现收敛不稳定状态,说明同样存在一个保证兼顾稳定性和正常收敛的允许步长范围.
3 结论
无论是固定步长盲源分离还是变步长加速的自然梯度盲源分离,在不同混合信号盲源分离保证兼顾稳定性和正常收敛的允许步长范围内,对于构成与分离输出状态紧密相关的变步长算法时,从分离信号峭度累积量变化的角度看,衡量自然梯度盲源分离稳定加速收敛的观察指标存在于分离信号峭度累积量随步长(固定步长或变步长)迭代变化量曲线e(k)的变化特征中,即e(k)变化率为0的开始迭代阶段和变化部分的集中程度是两个重要观察指标.当衡量构成与自然梯度盲源分离输出程度紧密关联的稳定加速方法的有效性时,该特征指标就是一个参考依据.

