一种非线性变步长LMS自适应滤波算法

仝喜峰，陈卫松，钱隆彦，肖梦迪

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241000)

0 引言

自适应主动噪声控制技术被认为是一种有效的噪声控制方法，并且在低频噪声控制领域取得了许多实际应用[1]。在自适应主动噪声控制系统中，多采用最小均方LMS算法[2-5]， LMS算法步长因子选取较大值时，算法可以获取较快的收敛速度，但是稳态误差较大；当步长因子选取较小值时，算法可以获取较小的稳态误差，但收敛速度较慢。固定步长值的固有缺陷无法合理协调收敛速度和稳态误差，各种变步长LMS算法陆续出现，其原理是在算法收敛过程中动态地改变步长值。文献[6]提出将步长值μ随算法迭代次数增大而减小，达到变步长调整的目的，但是这种步长调整规则仅适用于非时变的系统。文献[7]提出了一种基于Sigmoid函数的变步长SVSLMS算法，通过在步长和误差信号之间建立非线性关系，有效解决了文献[6]中面向系统的问题，但该算法在误差较小时，步长调整幅度较大导致算法不能保证较小的稳态失调。文献[8]在SVSLMS算法的基础上提出一种新的算法，解决了误差较小时步长调整过快的问题。

虽然变步长LMS算法种类繁多，但是对步长调整的原则大致相同。即在误差值大时(初始收敛阶段)，为了算法获得较快的收敛速度，步长取较大值；当误差小时(收敛完成阶段)，为了获取小的稳态误差，步长取较小值，以此来提高整个算法的性能[9-12]。本文在现有变步长LMS自适应滤波算法的理论基础上，通过引入步长因子与误差信号的非线性关系,提出了一种新的变步长LMS算法，并将其应用在电脑风扇低频噪声控制中。经仿真实验得知，针对电脑风扇噪声控制具有较好的效果。

1 变步长LMS算法

1.1 LMS自适应滤波算法

自适应滤波器结构[13]如图1所示。其中，x(n)为n时刻的输入信号，y(n)为自适应滤波器的输出信号，d(n)为n时刻的期望信号，通过期望信号d(n)与滤波器输出信号y(n)作差运算得到n时刻的误差信号e(n)，自适应滤波器根据误差信号的变化来自适应调节滤波器参数，直到自适应滤波器的输出信号y(n)无限接近期望信号d(n)。

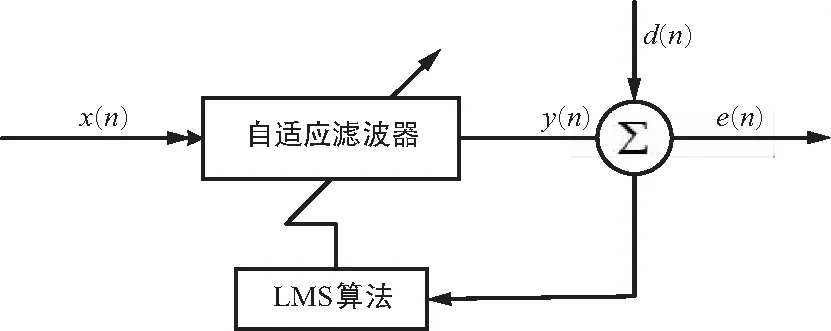
图1 自适应滤波器结构

LMS自适应滤波算法的基本步骤如下：

y(n)=WT(n)X(n)，

(1)

e(n)=d(n)-y(n)，

(2)

W(n+1)=W(n)+2μe(n)X(n)，

(3)

式中，μ为步长因子。

1.2 SVSLMS自适应滤波算法

在众多类型的变步长算法中，由覃景繁等人基于Sigmoid函数提出的变步长LMS算法是最为经典的一种，SVSLMS算法变步长函数表达式为[7]：

(4)

式中，变步长μ(n)为e(n)的sigmoid函数，α为控制函数形状的常数，β为控制函数取值范围的常数。通过在误差信号和步长之间建立新的非线性函数关系，克服了LMS算法收敛速度与稳态误差之间的矛盾。变步长函数μ(n)可以满足在算法收敛初期选取较大步长，在算法已经完成收敛状态，选取较小步长保证较小的稳态误差。使得算法可以在获得较快收敛速度的前提下，保证较小的稳态误差，并在跟踪能力上有了较大的提升。但SVSLMS算法在变步长函数设置上仍然存在一定的缺陷，在误差e(n)接近零处时，变步长函数变化太大，不具有缓慢变化的特性，使得SVSLMS算法在自适应稳态阶段仍具有较大的步长变化。基于此，文献[8]提出了一种改进的SVSLMS算法，步长调整函数为：

(5)

1.3 非线性变步长LMS算法

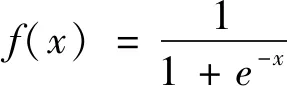
(6)

图2为sigmoid函数及调整过程中的非线性函数曲线，其中曲线1为Sigmoid函数曲线，曲线2为Sigmoid函数求导曲线，曲线3为曲线2翻转后的曲线，将曲线3向上平移0.5个单位长度得到最终的曲线4。

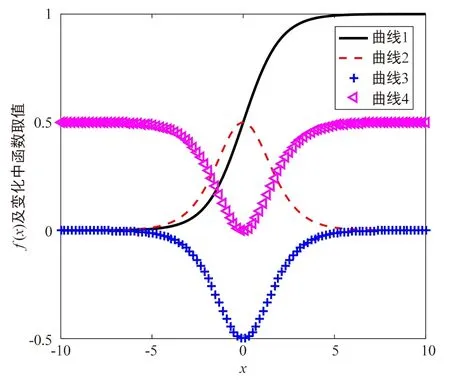
图2 sigmoid函数及调整过程中的非线性函数曲线

随着自变量的增大，函数的斜率呈现先增大后减小的特点，将其导函数取反得到曲线3，呈现先减小后增大的规律，向上平移得到最终函数曲线4。从图2可以发现曲线4满足非线性变步长函数的调整原则，在初始收敛阶段步长保持较大取值，在收敛完成阶段选择较小步长取值，并且在误差接近零处时，步长调整节奏缓慢。式(6)可以看做是一种新型的非线性变步长函数模型，为了更好地对其形状进行控制，本文将参数α，β引入公式中[14]，得到改进的非线性函数模型：

(7)

式中，参数β主要控制函数取值范围；α，β共同控制函数的形状。

1.4 3种算法对比分析

为了更加直观地对本文列举的3种算法变步长函数进行对比，图3(a)和图3(b)分别为3种算法的变步长函数与误差关系对比图和局部对比图，从图中可以看出，3种算法的迭代步长函数都能保证在误差较大的算法收敛初期提供较大的步长，提高算法的收敛速度；在误差较小(接近于0时)的算法收敛阶段提供较小的步长，保证算法收敛状态的稳定性。

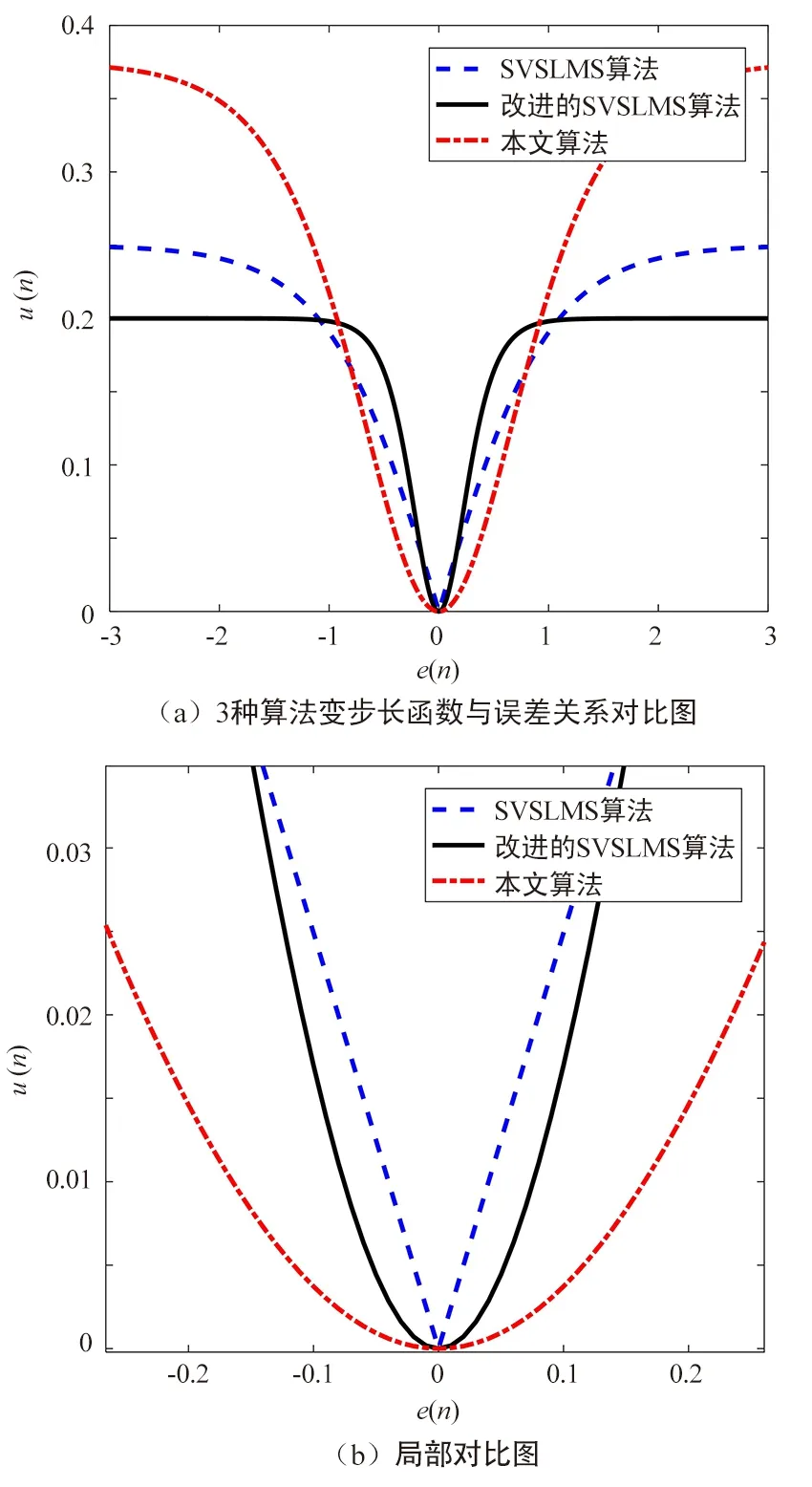
图3 3种算法对比图

从图3(a)可以看出，当算法初始收敛阶段(误差较大时)，本文算法的步长取值在3种算法中最大，确保了算法的收敛速度。对比3种变步长函数曲线可以看出，改进的SVSLMS算法和本文算法在误差信号趋于零时，步长变化相对较缓慢，确保算法可以获得较好的稳定性，本文变步长函数表现更优。

为了更好地分析本文提出的变步长函数中参数α，β的作用以及取值，下面分别讨论参数α，β对函数模型性能的影响，并分析其适当的取值范围。图4和图5分别为β相同、α不同，α相同、β不同2种情况下，变步长函数μ(n)与误差信号e(n)之间的关系曲线。

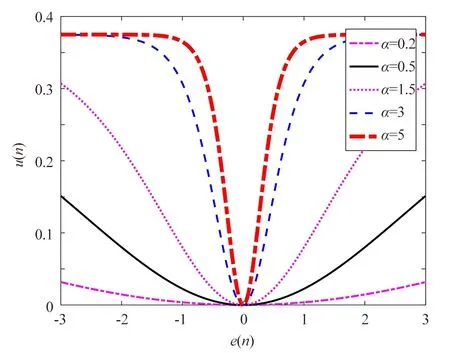
图4 μ(n)与e(n)的关系曲线(β相同、α不同)

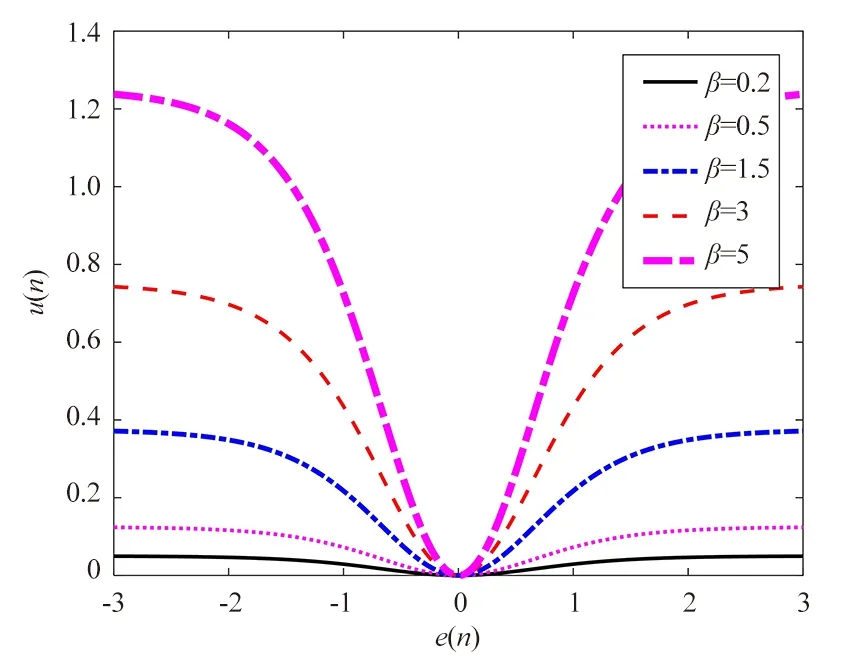
图5 μ(n)与e(n)的关系曲线(α相同、β不同)

图4为β取1.5时，α分别取0.2，0.5，1，3，5的步长因子与误差的函数曲线。图中多数曲线均能满足变步长取值的原则，在误差值大时(初始收敛阶段)，为了算法获得较快的收敛速度，步长取较大值；当误差小时(收敛完成阶段)，为了获取小的稳态误差，步长取较小值来提高整个算法的性能。此外，稳态误差与步长取是密切相关，当误差接近零处时，为了算法可以平稳收敛，保持较小的稳态误差，此时步长选取较小值，并且变化幅度较为平缓。显然图4中多数曲线均能满足这一点要求。

由上分析可见，α值越大，模型性能越优。但太大的α会使步长因子在误差较大时减到一个较小的值，从而使系统的收敛速度变慢。当α越小时，在稳态阶段算法可以获得较小的步长值，保证算法的稳定性，但在误差较大时却不能提供较大的步长值来加快算法的收敛速度。综合以上因素，α值宜在2.8～3.2范围内选取，本文选定α=3，此时算法在误差较大时,步长因子取值较大，保证了算法收敛速度较快，而在误差接近零时步长曲线也逐渐贴近零刻度线，并且变化幅度较为平缓，算法获得更高的稳定性。

图5为α取3时，β分别取0.2，0.5，1.5，3，5的步长因子与误差的函数模型曲线。从迭代步长与参数β关系图可以看出，对于相同的的初始误差，β取值越大，初始收敛阶段算法的收敛速度越快。若β取值过大，虽然收敛速度得到提高但是算法收敛后|e(n)|对应的步长μ(n)也较大，造成较大的稳态误差。如果在实际应用中对收敛速度的需求较高，则可以选用较大的β值；如果对稳态误差的需求较高，可选取较小的β值。但应当注意的是，当β取值过小时，步长μ(n)迭代变化区间较小，此时变步长LMS算法也就近似退化为固定步长LMS算法，收敛速度不会有较大提高。为分析方便，本文取α为定值3，β为变参数，μ(n)与β成正比，根据实际需求决定参数β的最优取值。

2 算法模拟仿真分析

为了检验本文算法的收敛速度和稳态误差性能表现，对算法进行仿真实验，并选取2种具有代表性的变步长LMS自适应滤波算法作为对比。

图6为3种算法的最小均方误差(MSE)变化曲线对比，从图中可见，在信噪比SNR分别为5,10,15三种噪声背景下，SVSLMS算法的收敛速度最慢，本文提出的算法在不同噪声环境下均能表现出较快的收敛速度。图6(a)在SNR=5低信噪比背景下，本文算法迭代80次左右就已经完成了算法的收敛过程，而SVSLMS算法及改进的SVSLMS算法完成整个收敛过程则需要迭代次数达到200次和150次。当信噪比较大时，本文算法提高收敛速度的优势将进一步扩大。

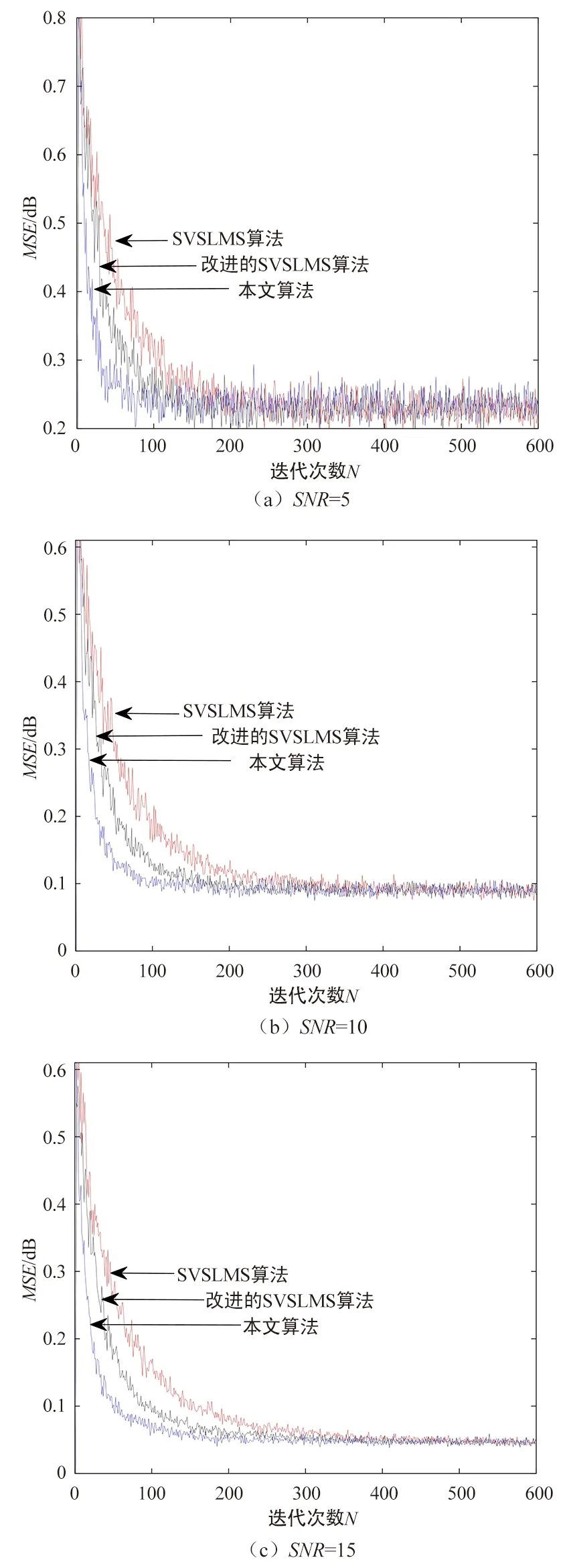
图6 不同信噪比背景下3种算法MSE对比

为了进一步检验算法在面对时变噪声背景时跟踪收敛能力的表现，仿真条件在算法迭代到500次时，未知系统发生时变，图7分别为不同信噪比背景下3种算法跟踪收敛能力的曲线对比。

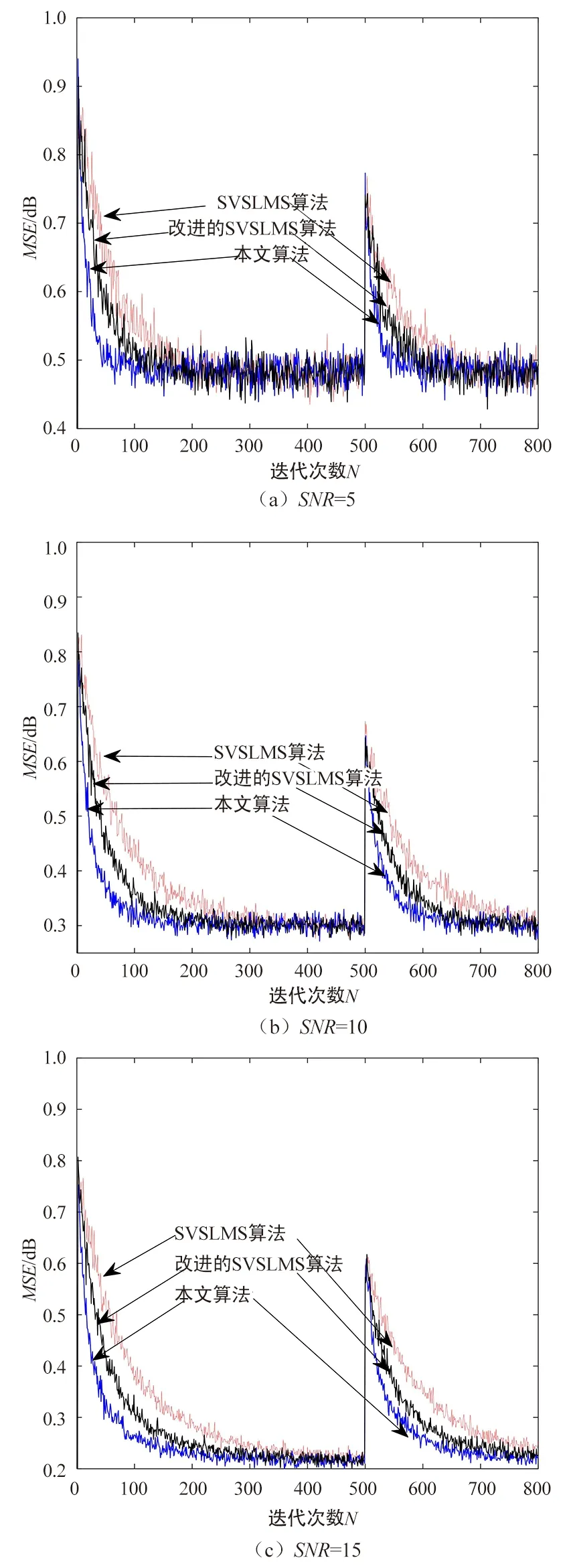
图7 3种算法跟踪收敛效果对比图

由图7 可以看出，当未知系统发生时变时，3种算法均能保持较好的跟踪能力。本文算法在3种算法中表现最优，并且随着信噪比的增加，这一优势也逐渐拉大。

为了分析本文提出算法在实际噪声环境中的应用效果，录制了一段电脑风扇噪声并导入Matlab程序，采用本文算法对噪声进行有源噪声控制。在实际仿真中设置信噪比SNR=5 dB，滤波器长度为8。

图8为3种算法作用下电脑风扇残余噪声时域图。从图中可以看出,SVSLMS算法完成收敛需要迭代120次，改进SVSLMS算法则需要80次，而本文算法在迭代50次左右就已完成收敛。除此之外，本文算法的鲁棒性也明显的优于其他2种算法。

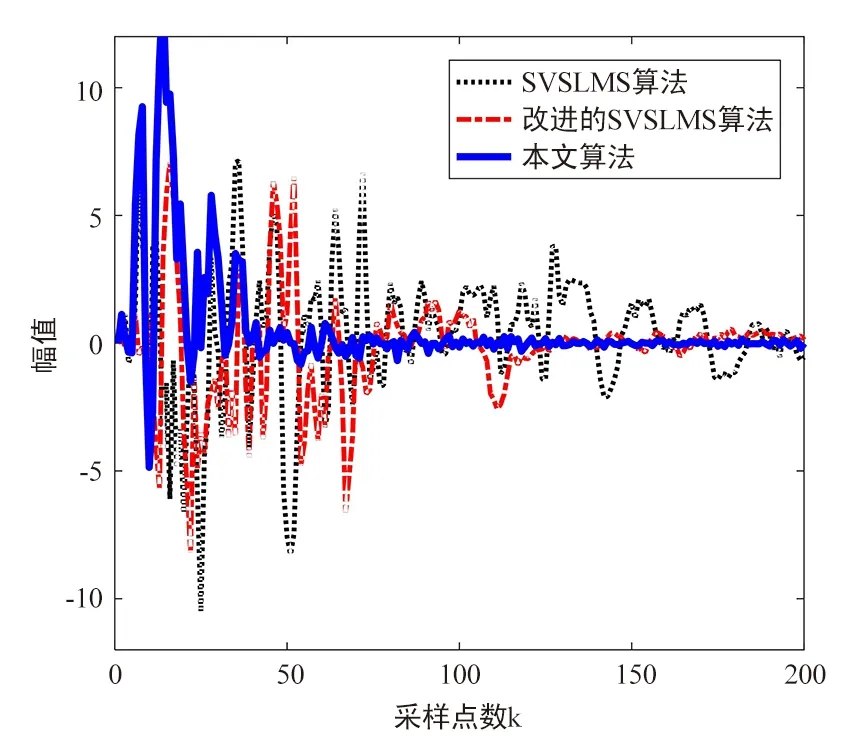
图8 电脑风扇残余噪声时域图

3 结束语

通过在误差信号与步长之间建立另一非线性关系，本文提出了一种新的变步长LMS自适应滤波算法，达到了动态改变步长大小的目的，并且分析了变步长函数中参数α,β对算法收敛的影响以及取值原则。实验仿真结果表明，本文算法有效克服了SVSLMS算法在收敛阶段步长变化过快的弊端，与改进的SVSLMS算法相比，虽然计算量有所增加，但可以获取更好的收敛效果。该算法在后期需要在算法复杂度方面进行优化，减小算法的计算量。