复Hessian矩阵性质及复正定性的研究

张宋传

（武夷学院 数学与计算机学院，福建 武夷山 354300）

考虑复变量优化问题：

其中，优化变量z取值范围是复数域，目标函数为复变量实值函数。不同于实变量优化问题，问题(1)中目标函数在非常值情形下，不满足柯西-黎曼条件[1]，因此传统的复变函数微分理论无法应用于复变量优化问题的算法设计和理论分析上。早在20世纪初，Writinger便提出了一种扩展的复变函数微分理论[2]。直到上世纪80年代，随着复变量优化问题在工程应用领域的广泛出现，Writinger微分理论逐渐成为复变量优化问题研究的一个重要理论工具[5-9]。Brandwood首次引入复梯度的概念[3]，A.van den Bos进一步给出复Hessian矩阵及复域上泰勒展开式[4]，Kreutz-Delgado系统总结了前人的成果，将Writinger微分理论命名为R-微分，而将传统的复变函数微分理论称为C-微分，二者统称CR微分[10]。

问题(1)中目标函数复Hessian矩阵的相关性质，尤其是复Hessian矩阵的复正定性研究非常有意义，例如，使用复Hessian矩阵的复正定性可以判断函数凸性与否，即问题(1)是否可收敛到局部/全局的最优解。此外，复Hessian矩阵的复正定性在判断优化算法可行性时非常有用。关于复变实值函数的复Hessian矩阵定义最早出现在文献[4]中，文献[10]指出复Hessian矩阵的定义是不唯一的，复Hessian矩阵相关性质的研究可以参考文献[9-12]。在已有的研究基础上，进一步讨论复变实值函数复Hessian矩阵的一些性质，并给出复Hessian矩阵复(半)正定与Hermite(半)正定的一些充要条件。

1 预备知识

本文中，用 Cm×n与 Rm×n分别表示 m ×n 复矩阵集与实矩阵集，(·)T，，(·)H分别表示矩阵或向量的转置，共轭及共轭转置，Re(·),Im(·)分别表示复值对象的实部和虚部。n维复向量z与其共轭向量定义如下:

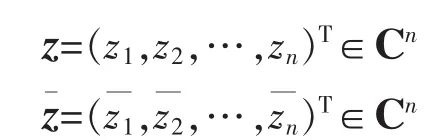
其中，zi=xi+j yi，i=1,2,…,n，j为虚数单位，即或者，z=x+j y,z=x-j y

其中，

则v=J w，辅助矩阵J定义为

其中，In表示n阶单位阵。显然，J是可逆阵，有JH，因此，w=

R微分中，考虑复变实值函数_的导数与微分时，形式上将复变量z∈Cn与它的共轭z认为是两个独立的变量。

定义 1[10]设函数 g（z）:Cn→ C ，g（z）关于 z与 z的R导数与R导数分别定义为:

定义 2[10]设函数 g（z）:D⊆ Cn→ C，设 c是 D 的一个内点，如果存在 c 的一个球邻域 B（c），B（c）中任一点的R导数与导数都存在，并且c点的R导数与导数在c点上连续，则称函数g（z）在点c上是R可微的；如果D是Cn中的开子集，函数g（z）在D上任一点上都R可微，则称g（z）在D上是R可微的。

定义3[10]设D是Cn中的开子集，则函数g（z）:D→C，在D上二阶R可微当且仅当R导数与导数在D上是R可微的。

定义 4[10]设函数g（z）:D⊆Cn→C在D内关于z与z的二阶导数R与导数存在，则g（z）的复Hessian矩阵定义为

注 1:g（z）的复Hessian矩阵定义是不唯一的，最早出现在文献[4]_中，其v的结构定义为

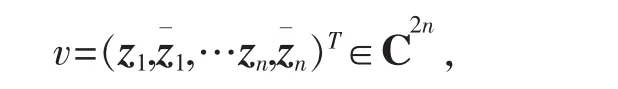
这在实际应用中不是很方便。 Kreutz-Delgado在文献[10]中给出另一个定义，

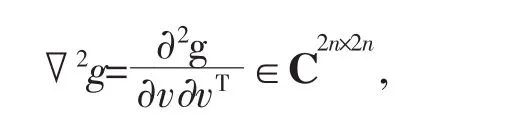
和定义4的最大不同只表现在g（z）的二阶泰勒展开式的不同。为了讨论方便，本文只采用定义4中的形式。

R 微分中，g（z）常常写作 g（z，z）。另一方面，g（z）也可视为实变函数g（x,y），其中z=x+j y，习惯上我们使用不同的函数名予以区分，此处使用 f（x,y）或 f（w）表示，同时记▽2f∈ R2n×2n为 f（x,y）的实 Hessian 矩阵。

定义 5[13]设 A∈ R2n×2n，如果对任意非零 ξ∈ Rn，都有ξHAξ≥0，则称A为实半正定矩阵。若上式取严格不等号，则称A为实正定矩阵。

定义 6[13]设 A∈ Cn×n，如果对任意非零 ξ∈ Cn，都有Re（ξHAξ）≥ 0，则称A 为复半正定矩阵。若上式取严格不等号，则称A为复正定矩阵。

易知，如果 A∈ Rn×n，则 A 为复（半）正定矩阵当且仅当A为实（半）正定矩阵。

定义 7[13]设A∈Cn×n，AH=A，如果对任意非零ξ∈ Cn，都有 ξHAξ≥ 0，则称 A 为 Hermite半正定矩阵。若上式取严格不等号，则称A为Hermite正定矩阵。

显然，Hermite（半）正定矩阵是复（半）正定矩阵。

引理 1[14]若A为复（半）正定矩阵，对任意同阶可逆阵P，PHAP为复（半）正定矩阵。

2 主要结果

定理 1 设函数 g（z）:D⊆Cn→R在 D 内关于 z与 z的二阶R导数与导数存在，则f（x,y）在实域~D内关于x与y的二阶偏导数存在，且

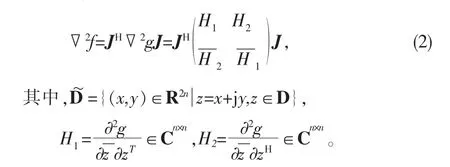
证明见文献[11]命题4，事实上，证明中仅用到二阶导数与导数存在这一事实，因此本文定理1将原结论条件由“函数 g（z）:D⊆Cn→R在D上二阶 R可微”减弱为“函数 g（z）:D⊆ Cn→R 在 D 内关于 z与的二阶R导数与导数存在”。

定理 2 设函数g（z）:D⊆Cn→R在D 上二阶R可微，则进而▽2g=（▽2g）H，即▽2g 是Hermitian阵，同时，▽2f为实对称阵。

证明：由于函数 g（z）:D⊆Cn→R在D上二阶R可微，根据 Hessian 矩阵对称性定理[15]，∀ i，k∈ ｛1,2,… ,n｝有再由定理1易知结论成立。

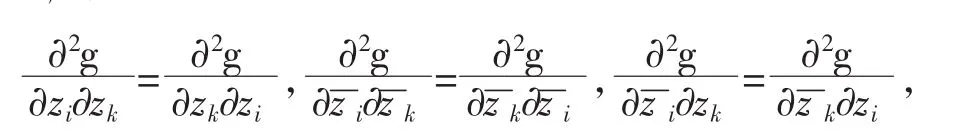
定理 3 设函数g（z）:D⊆Cn→R在D 内关于z与的二阶R导数与导数存在，▽2g是复(半)正定当且仅当▽2f是实(半)正定。

证明：J为可逆阵，且▽2f=JH▽2g J，由引理1得。

定理 4 设函数g（z）:D⊆Cn→R在D 内关于z与的二阶R导数与导数存在，▽2g是复半正定的当且仅当

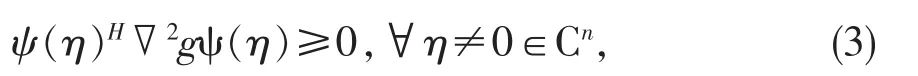
证明：不失一般性，我们仅考虑复半正定的情形。如果▽2g是复半正定的，∀η≠0∈Cn，由定义6可得Re（ψ（η）H▽2gψ（η））＝ψ（η）H▽2gψ（η）≥ 0，(3)式成立。

反之，如果(3)式成立，∀ ξ∈ R2n，且 ξ≠ 0，由定理1，有 ξH▽2fξ=ξHJH▽2g Jξ，因为

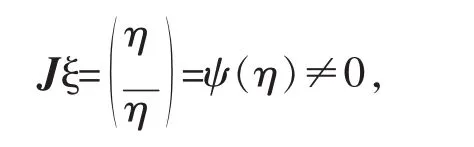
故有 ξH▽2fξ=ψ（η）H▽2gψ（η）≥ 0，即▽2f是实半正定的，由定理3知，▽2g是复半正定，证毕。

考虑到

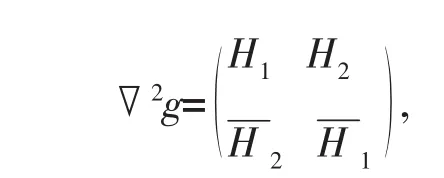
进一步有：

推论1▽2g是复半正定的当且仅当

Re（ηHH1η）+Re（ηHH2≥ 0,∀η≠ 0∈ Cn；▽2g是复正定的当且仅当上式不等号严格成立。

结合定理2，我们有

推论 2 设函数g（z）:D⊆Cn→R在D 上二阶R可微，▽2g是Hermite半正定矩阵当且仅当

（ηHH1η）+Re（ηHH）≥ 0,∀ η≠ 0∈ Cn；▽2g是Hermite正定矩阵当且仅当上式不等号严格成立。

3 例子

考虑如下复变量优化问题：

其中,b∈ Cm，A∈Cn×n是行满秩的。文献[11]提出一种复值拉格朗日神经网络算法解该类优化问题，若▽2g是复正定的，则复值拉格朗日神经网络是李雅普诺夫意义下全局渐进稳定的，输出轨迹全局收敛到问题的最优解。本节给出两个具体的复变量优化问题，目标函数的复Hessian矩阵的正定性判定将应用第二节中的主要结果，并通过复值拉格朗日神经网络算法求解，实验进一步证实上述结果的有效性。

例 1 考虑 g（z）=Re（zHMz）+Re（qHz），其中 q∈ Cn,M ∈ Cn×n是复正定矩阵，计算得

由推论1可知，▽2g是复正定矩阵。任取初始点，求解该问题的复值拉格朗日神经网络是李雅普诺夫意义下全局渐进稳定的，输出轨迹全局收敛到问题的最优解。图1展示了一数值实验中，任取10个随机初始点，输出解的目标函数值 g（z（t））的收敛过程。

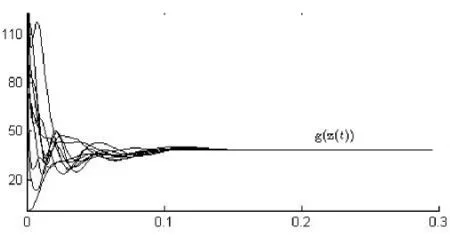
图1 复值拉格朗日神经网络输出解的目标函数值的收敛过程Figure 1 Transientbehaviors of g（z(t)）based on the complex-valued Lagrange neural network

例2考虑

∀ η≠ 0∈ Cn，易证得

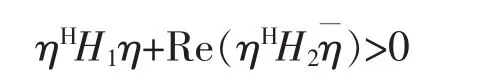
由推论2可知，▽2g是Hermite正定矩阵。图2展示了任取10个随机初始点，求解该问题的复值拉格朗日神经网络输出解z（t）的收敛过程。

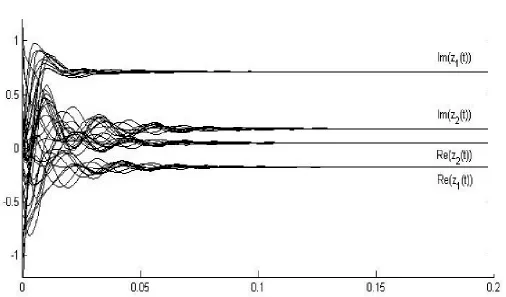
图2 复值拉格朗日神经网络输出解的收敛过程Figure 2 Transientbehaviors of z(t)based on the complex-valued Lagrange neural network