一类蜘蛛树的(k,d)-优美标号

张明军

(兰州财经大学 信息工程学院，甘肃 兰州 730020)

一类蜘蛛树的(k,d)-优美标号

张明军

(兰州财经大学 信息工程学院，甘肃 兰州 730020)

(k,d)-优美标号因为参数k,d可以取很多值，从而使得一些优美图是(k,d)-优美标号的特例.本文给出了(k,d)-优美标号的概念，定义了T(n+1,m)-蜘蛛树，并证明了T(n+1,m)-蜘蛛树不同情形下的(k,d)-优美标号．

(k,d)-优美标号；蜘蛛树；边标号

随着计算机的发展, 图的标号在网络和通讯等领域中的应用越来越广泛[1-2], 而图的各种标号已发展到许多种[3-7], 其中(k,d)-优美标号因为参数k,d可以取很多值，从而使得一些优美图是(k,d)-优美标号的特例，所以研究(k,d)-优美标号就变得重要而有意义.本文讨论了一类蜘蛛树不同情形下的(k,d)-优美标号.本文涉及的图均为有限、无向、简单图．文中没有定义的术语和符号均采用文献[3]．为了叙述简便，记一个有p个顶点，q条边的连通图为(p,q)-图.本文中用记号[m,n]表示非负整数集{m,m+1,m+2,…,n}, 其中m和n均为整数.

对于一棵树T，如果存在一个映射f:V[T]→[0,k] ，使对不同的顶点x,y∈V(T) ，有f(x)≠f(y) ，并且每条边uv分配标号f(uv)=|f(u)-f(v)| ，且使得边标号互不相同，则称f是T的一个正常标号．树T的顶点、边标号分别记为f(V(T))={f(u)|u∈V(T)} 和f(E(T))={f(u)|uv∈E(G)}．如果树T只有一个顶点ω满足dT(ω)≥3，且对任意v∈V(T){ω}，有dT(v)≤2，那么这棵树T称为蜘蛛树，顶点ω为蜘蛛树T的中心.

定义1[1]如果一棵n个顶点的树T有一个正常标号f:V[T]→[0,n-1]，使得边标号集合{f(uv)|uv∈E(T)}=[1,n-1]，则称T为优美树，f是T的一个优美标号．

定义2[2]设G是(p,q)-图，若存在映射f:V(G)→[0,k+(q-1)d]，使得边标号集合f(E(G))={k,k+d,…,k+(q-1)d}，则称f是G的一个(k,d)-优美标号．

下面给出本文的研究对象：以v0为顶点，有n+1条腿，且腿长(除腿vv0)为m的蜘蛛树称为T(n+1,m)-蜘蛛树， 如图1所示.

图1 T(n+1,m)-蜘蛛树Fig.1 T(n+1,m)-spider tree

主要结果及证明如下：

定理1T(n+1,2)-蜘蛛树是(k,d)-优美标号．

证明给出T(n+1,2)-蜘蛛树的标号：f(v)=0 ；f(v0)=k+2nd；f(vi,1)=id, (i=1,2,3,…,n)；f(vi,2)=k+(2i-1)d, (i=1,2,3,…,n)．

下面证明T(n+1,2)-蜘蛛树是(k,d)-优美标号：

(1)由上面标号可知f最大为f(v0)=k+2nd，最小为f(v)=0；所以f(V(T))=[0,k+2nd]．

(2)在T(n+1,2)-蜘蛛树的边标号中没有相同的标号.

f(v0v)=f(v0)-f(v)=k+2nd；

f(e1)=f(v0)-f(vi,1)=k+(2n-i)d；

f(e2)=f(vi,2)-f(vi,1)=k+(i-1)d.

下面分三种情形证明.

情形Ⅰ.T(n+1,2)-蜘蛛树中没有与腿v0v相同的边标号.

因为f(v0v)-f(e1)=id≠0 (i=1,2,…,n)；

f(v0v)-f(e2)=(2n-i+1)d≠0(i最大为n)，(i=1,2,…,n).

所以T(n+1,2)-蜘蛛树中没有与腿v0v相同的边标号.

情形Ⅱ.T(n+1,2)-蜘蛛树的同一条腿上没有相同的边标号.

因为f(e1)-f(e2)=(2n-2i+1)d≠0(i最大为n)，(i=1,2,…,n).

所以T(n+1,2)-蜘蛛树的同一条腿上没有相同的边标号.

情形Ⅲ.T(n+1,2)-蜘蛛树的任意两条不同腿上没有相同的边标号.

在T(n+1,2)-蜘蛛树的不同腿上任取两点i,j∈V(T)，(i,j=1,2,…,n;且i≠j)，则

|f(e1)-f(e2)|=|i-j|d≠0 (i≠j)；

或

|f(e1)-f(e2)|=|2n+1-i-j|d≠0 (i+j最大为2n)，(i,j=1,2,…,n).

即T(n+1,2)-蜘蛛树的任意两条不同腿上没有相同的边标号.

综上所述,在T(n+1,2)-蜘蛛树的边标号中没有相同的标号, 即

f(E(T))={k,k+d,…,k+2nd}.

故T(n+1,2)-蜘蛛树是(k,d)-优美标号．

图2、图3是解释定理1的两个例子.

图2 T(3+1, 2)-蜘蛛树Fig.2 (k-d) graceful labelling of T(3+1,2)-spider tree

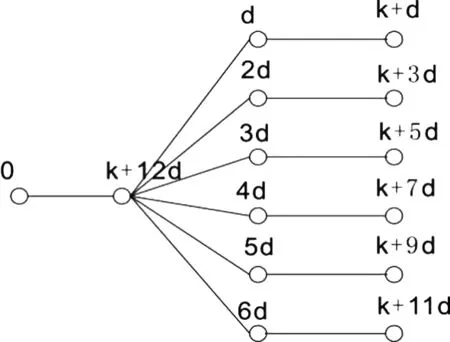
图3 T(6+1, 2)-蜘蛛树的Fig.3 (k-d) graceful labelling of T(6+1,2)-spider tree

定理2T(n+1, 3)-蜘蛛树是(k,d)-优美标号．

证明给出T(n+1,3)-蜘蛛树的标号：f(v)=0 ；f(v0)=k+3nd；

f(vi,1)=id, (i=1,2,3,…,n)；f(vi,2)=k+(n+2i-1)d, (i=1,2,3,…,n)．

f(vi,3)=(n+i)d, (i=1,2,3,…,n)

下面证明T(n+1,3)-蜘蛛树是(k,d)-优美标号：

(1)由上面标号可知f最大为f(v0)=k+3nd，最小为f(v)=0；所以f(V(T))=[0,k+3nd]．

(2)下面证明在T(n+1,3)-蜘蛛树的边标号中没有相同的边标号.与定理1相同，本题也分三种情形证明.即

情形Ⅰ：T(n+1,3)-蜘蛛树中没有与腿v0v相同的边标号；

情形Ⅱ：T(n+1,3)-蜘蛛树的同一条腿上没有相同的边标号.

情形Ⅲ.T(n+1,3)-蜘蛛树的任意两条不同腿上没有相同的边标号.(只证明情形Ⅲ)

在T(n+1,3)-蜘蛛树的不同腿上任取两点i,j∈V(T)，(i,j=1,2,…,n;且i≠j).

f(ei)=f(v0)-f(vi,1)=(3n-i)d

或f(ei)=f(vi,2)-f(vi,1)=k+(n+i-1)d

或f(ei)=f(vi,2)-f(vi,3)=k+id；

f(ej)=f(v0)-f(vj,1)=(3n-j)d

或f(ej)=f(vj,2)-f(vj,1)=k+(n+j-1)d

或f(ej)=f(vj,2)-f(vj,3)=k+jd.

则|f(ei)-f(ej)|=|i-j|d≠0 (i≠j)

或|f(ei)-f(ej)|=|k-(2n-i-j+1)d|≠0(i+j最大为2n)

或|f(ei)-f(ej)|=|k-(3n-i-j)d|≠0 (i+j最大为2n)， (i,j=1,2,…,n).

即T(n+1,3)-蜘蛛树的任意两条不同腿上没有相同的边标号.

综上所述, 在T(n+1,3)-蜘蛛树的边标号中没有相同的标号, 即

f(E(T))={k,k+d,…,k+3nd}.

故T(n+1,3)-蜘蛛树是(k,d)-优美标号．

图4、图5是解释定理2的两个例子

图4 T(3+1, 3)-蜘蛛树是(k,d)Fig.4 (k-d) graceful labelling of T(3+1,3)-spider tree

图5 T(6+1,3)-蜘蛛树Fig.5 (k-d) graceful labelling of T(6+1,3)-spider tree

定理3T(3+1,m)-蜘蛛树是(k,d)-优美标号．

证明给出T(3+1,m)-蜘蛛树的标号：f(v)=0 ；f(v0)=3md；

f(v1,j)=(1.5j-0.5)d,(j=1(mod2))；

f(v1,j)=k+(3m-1.5j-2)d, (j=0(mod2))；

f(v2,j)=(1.5j+0.5)d, (j=1(mod2))；

f(v2,j)=k+(3m-1.5j)d, (j=0(mod2))；

f(v3,j)=(1.5j+1.5)d, (j=1(mod2))；

f(v3,j)=k+(3m-1.5j+2)d, (j=0(mod2)), (j=1,2,…,m).

(T(3+1,m)-蜘蛛树是(k,d)-优美标号的证明与定理1、2类似，此处证明略)．

图6、图7是解释定理3的两个例子.

图6 T(3+1, 6)-蜘蛛树是(k,d)-优美标号Fig.6 (k-d) graceful labelling of T(3+1,6)-spider tree

图7 T(3+1 , 9)-蜘蛛树的边对称树的强优美标号Fig.7 (k-d) graceful labelling of T(3+1,9)-spider tree

[1] BLOOM G S， GOLOMB S W. Applications of numbered graphs[J]. Proceedings of the IEEE, 1977,65(4):562-570.

[2] Gallian J A. A Dynamic Survey of Graph Labelling [J].The Electronic Journal of Combatorics , 2009,12:42-43.

[3]YAO B, CHENG H， YAO M. A Note on Strongly Graceful Trees[J]. Ars Combinatoria, 2009,92: 155-169.

[4]周向前，姚兵，陈祥恩.探讨奇优美树猜想[J].山东大学学报(理学版)，2012(12):31-36.

[5]ZHOU X Q, YAO B，CHEN X E. Every Lobster Is Odd-elegant[J]. Information Processing Letters, 2013,113(1/2):30-33.

[6]姚明，姚兵，杨思华.关于树的二分优美标号[J].兰州大学学报(自然科学版)，2014,50(6):875-880.

[7]张明军，赵喜杨，姚兵.(2m+1,1)-p-树的二分强优美性和二分强奇优美性[J].应用数学学报,2016,39(3):419-428.

(k,d)-gracefulnessofspidertree

ZHANG Ming-jun

(School of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou 730020, China)

(k,d)-graceful labeling’s parametersk,dcan be taken to a lot of values. It makes some graceful graphs is special cases of (k,d)-graceful labeling. This paper presented the concept of (k,d)-graceful labeling， definedT(n+1,m)-spider tree，and proved (k,d)-graceful labeling in different situations ofT(n+1,m)-spider.

(k,d)-graceful labelling; spider tree; edge label

2017-01-11

国家自然科学基金项目(61662066)；兰州财经大学高等教育教学改革研究重点项目(LJZ201707)；甘肃省高等学校科研项目(2017A-047)

张明军，男，zhangmjlz@163.com

1672-6197(2018)01-0061-03

O157.5

A

(编辑：姚佳良)