一种新型积分滑模控制器在PMSM驱动的PEV调速系统中的应用

张 鹏，张 宏，倪振松

(福建师范大学 福清分校电子与信息工程学院，福建 福清，350300)

纯电动汽车拥有良好的节能、环保和低排放潜力，近几年得到工业界和学界的普遍重视。纯电动汽车有两个重要性能指标，分别是可靠性和精度控制[1]，而这两个性能指标的提高依赖于其驱动技术的发展。永磁同步电动机(permanent magnet synchronous motor，PMSM)具有转矩密度高、控制精度高、机械能转换效率高等优点，因而其广泛应用于纯电动汽车驱动系统中[2]。当前纯电动汽车驱动系统大多采用基于PID控制的矢量控制系统，然而矢量控制对被控系统的参数变化比较敏感，当被控系统参数发生变化时，那么就会破坏原有的解耦关系，从而使得矢量控制下的系统偏离预先设定目标。同时，PMSM是一个具有多个变量、参数时变、强耦合的非线性系统[3]，因此对于包含这种复杂的非线性对象的纯电动汽车使用PID控制结合矢量控制只能在特定范围内满足控制需求。然而当系统受到外界不确定因素干扰或者当系统固有参数发生变化时，此时采用PID控制结合矢量控制并不能满足高性能控制需求。针对传统的采用PID控制结合矢量控制的不足，学者提出各自的改进方案。文献[4]将电机矢量控制调速范围分为两个区间，分别是低速区间和高速区间，针对不同区间的电机电气特性，电流环采用不同控制算法。文献[5]将SVPWM调制策略和DPWM调制策略结合起来，在电机低调制比阶段运用SVPWM调制策略，而在电机高调制比阶段运用DPWM调制策略；并提出一种基于零矢量分配的过渡策略，使得两种调制方式可以平滑的过渡。文献[6]采用单神经元 PID 控制器和模型参考自适应相结合的控制策略，其中单神经元的输入是给定转速和估算转速之差，利用神经元的学习特性对PID参数进行在线学习。文献[7]提出一种基于分数阶PI控制器来改善电机调速性能。文献[8]提出了一种基于自适应粒子群算法的模糊PI速度控制器的参数优化的方法，在模糊PI控制器中，PI参数的优化是通过自适应粒子群算法对模糊隶属函数的优化来实现的。文献[9]利用遗传算法优化鲁棒H∞控制器中的加权函数，从而使得电动汽车调速系统获得较小的干扰波动和卓越的车速跟踪性能。文献[10]设计了状态相关黎卡提方程(SDRE)控制方法，并应用泰勒级数法进行了解算，该方案不仅可以减少速度控制稳态误差，还能提高系统的响应速度。

根据目前电动汽车对其驱动调速系统的要求是运行稳定可靠、调速快这些要求，同时结合纯电动汽车包含PMSM这种非线性、多变量、强耦合、变参数的复杂对象，调试系统引入滑模控制(Sliding Mode Control)。滑模控制隶属非线性控制，由于基于滑模控制器的被控系统的“结构”是变化的、不固定的，因此滑模控制也被称为变结构控制。滑模控制器能够根据被控系统此刻的状态不断调整控制器结构，一旦系统偏离预定轨迹，即预先设定的“滑动模态”，那么系统将被“拉回”到滑动模态上运动。由上述滑模控制的特性，可知滑模控制器的设计与被控对象的参数无关，同时滑模控制能够克服外界对系统的干扰，能够使得系统按照预定轨迹运动。同时滑模控制器物理实现相对较简单、动态响应性能良好等优点[11]。

本论文尝试在PMSM驱动的PEV速度环控制器中引入滑模控制，同时将速度误差信号的积分导入到滑模控制器中，从而增强系统的抗干扰能力；提出一种新型的趋近律，有效地抑制了滑模固有的抖振现象；采用基于改进的函数切换控制的滑模控制方案，根据误差大小来决定是否引入切换控制，在一定程度上降低抖振。仿真结果表明，基于积分滑模控制的控制系统具有良好的动态、稳态性能以及较强的鲁棒性，与传统PID控制器相比，具有更快的起动响应速度，更精确更快速地跟踪速度。对于实际控制系统的设计和实现提供了一定的理论基础，具有一定的工程参考价值。

1 数学模型

1.1 PMSM的数学模型

由于PMSM是一个多变量，且多变量之间高度耦合的非线性系统，针对耦合的非线性系统，通常采用解耦控制。目前最常用的解耦控制是采用id=0的转子磁场控制。在该控制策略下，永磁同步电机输出转矩的大小只和定子电流有关，从而使得控制永磁同步电机转矩也像控制直流电动机一样简单方便。被控对象数学模型的建立，通常要抓主要因素影响，因此在不影响电机控制性能的前提下，忽略电机内部涡流损耗以及电机内部磁滞等次要因素影响，建立PMSM在d-q轴下的数学模型[12]：

(1)

id=0

(2)

(3)

电磁转矩公式为：

Te=3npLmdIdfiq/2

(4)

id、iq分别为定子电流d、q轴分量,uq为定子电压q轴分量,Rs为定子电阻,Lq为定子q轴电感,ωr为转子机械角速度,Lmd为d轴的互感,Idf为d轴等效磁化电流,np为极对数,Te为电机输出电磁转矩,Tl为电机负载转矩,Bm为电机摩擦系数,J为电机转动惯量。

从上述数学模型，可以看出电机输出电磁转矩Te正比于q轴电流，这样就可以通过控制q轴电流来控制电机输出电磁转矩，从而实现了电机的解耦控制。

(5)

(6)

结合电机系数的不确定性，状态方程转化为如下形式：

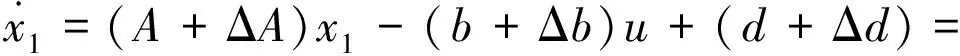
(7)

1.2 电动汽车及驱动系统的数学模型

要对纯电动汽车调速系统进行控制研究，首先需要确定的是被控对象纯电动汽车的数学模型。国内外很多学者研究纯电动汽车建模，提出相应数学模型[13-14]，根据他们提出的数学模型，结合汽车在行驶过程中存在力的平衡，即可得出如下方程：

Ft=∑F

(8)

其中等式中Ft为驱动力，∑F为行驶阻力之和。把公式(8)代入驱动力方程、总阻力方程、行驶方程、转速方程，最终得到如下方程：

(9)

其中，CD为大气阻力系数，r为车轮半径，V为汽车行驶速度，A为迎风面积，Te为电机转轴输出转矩，ig为变速器传动比，ma为电动汽车总质量，g为地球重力加速度，io为主减速器传动比，ηT为传动系统效率，f为滚动阻力系数，α为行驶道路坡度角，δ为电动汽车旋转质量转换系数，n为电机输出转速。

io=(0.377nmaxr/igVmax)

(10)

依据上面公式，在MATLAB/simulink中对电动汽车进行建模，电动车的仿真模型如图1所示，车速与电机转速关系如图2所示。

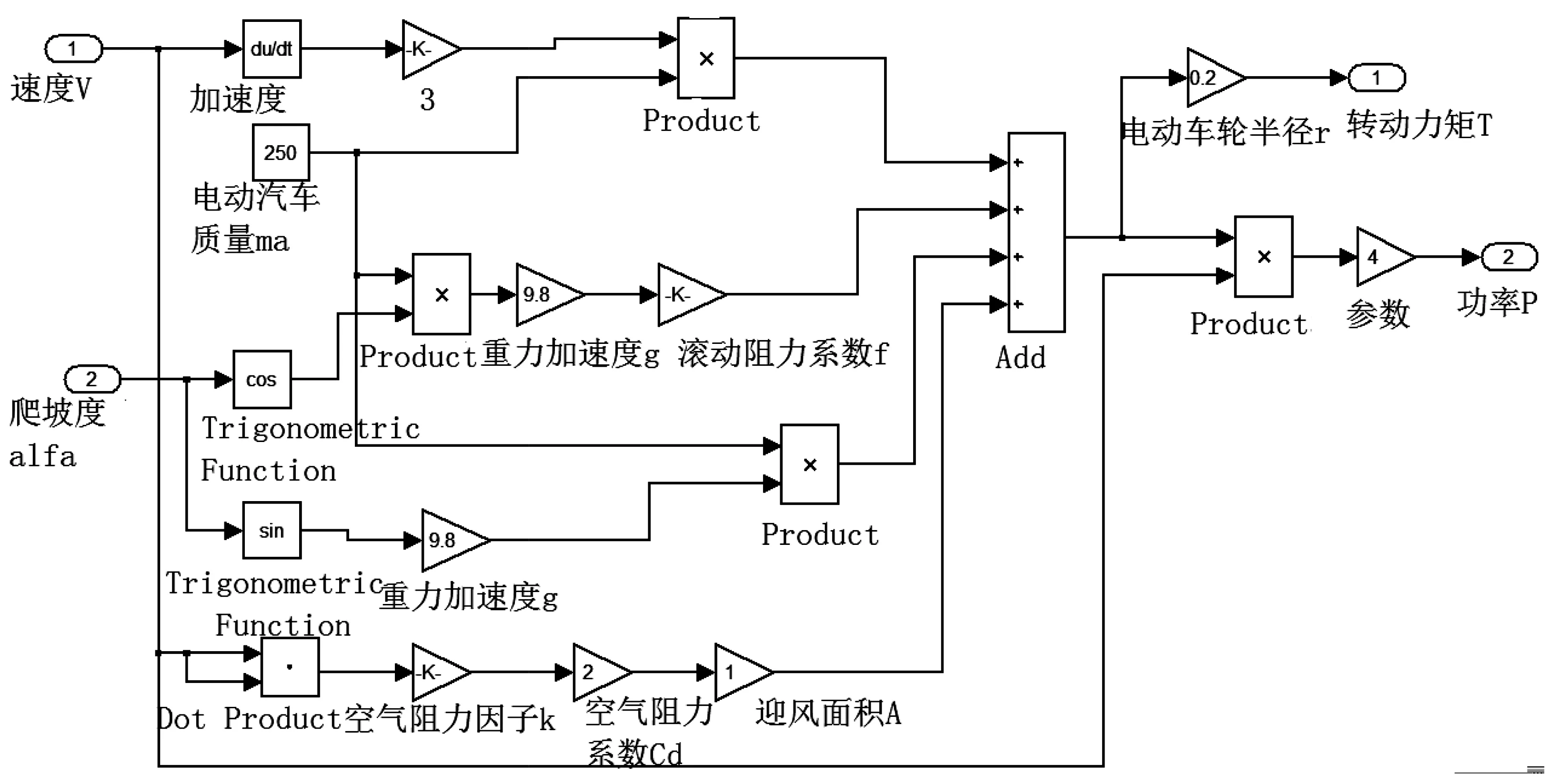
图1 纯电动汽车仿真模型Fig.1 The simulation model of pure electric vehicle

图2 车速和电机转速关系模型Fig.2 The relation model between car speed and motor speed

2 新型积分滑模控制器的设计

设计滑模控制器主要有两个步骤[15]：一是设计切换函数，二是设计滑动模态控制率。

切换函数的作用在于针对系统设计的滑动模态能够保证系统渐进趋于稳定，同时渐进过程具有良好的动态性能；滑动模态控制律主要作用在于使系统在有限的时间内到达并保持在滑动模态切换面上。

(1)确定切换函数S(x)。

积分滑模具有削弱滑模控制产生的抖振、降低稳态误差，平滑电机输出转矩以及提高滑模控制器的稳定性等优点，因此通过在切换函数中引入积分滑模来确保系统的滑动模态具有良好的动态品质和渐进稳定性。

积分滑模控制器切换函数S(x)的基本形式如下：

(11)

其中c为正常数，c值的大小直接影响着被控系统趋于稳定的时间。c值越小，系统趋于稳定的时间越长，反之，c值越大，系统趋于稳定的时间越短，然而过大的c值会加剧滑模控制所产生的抖振。因此c值的选取需要依据实际需求情况来确定。

(2)确定滑模控制律u±(x)。

通过在系统中引入改进型积分滑模控制中的函数切换控制，来缩短被控系统状态到达滑动模态切换面的时间。改进型函数切换控制的数学表达式为u=ueq+η*ud，该数学表达式分为三个部分。第一部分为滑模等效控制ueq，其作用为使被控系统状态保持在滑模面上；第二部分为滑模切换控制ud，该部分能将偏离滑模面的系统状态变量拉回滑模面并最终稳定下来；第三部分为切换控制开关η，当系统状态在距离滑模面很近或者在滑模面上，则关闭切换控制，即η=0，这样就可以避免因为很小状态误差引起的频繁切换控制，在一定程度上抑制了抖振。

2.1 滑模控制律等效控制部分的确定

滑模控制等效控制部分通常是在忽略被控系统环境外加干扰项d和系统的不确定项ΔD的情况下设计的，此时被控系统的状态方程化简为如下形式：

(12)

被控系统在滑模面上滑动时有

(13)

并将式(13)代入式(12)，可以得到

(14)

2.2 滑模切换控制部分的确定

由上节可知，滑模控制中的等效部分是基于忽略外加干扰d和系统的不确定项ΔD的情况下设计，然而外加干扰d和系统的不确定项ΔD的存在会使得被控系统状态偏离预先设定的滑模面，因此在本节中通过滑模控制中的切换控制部分来克服外加干扰d和系统的不确定项ΔD的影响，滑模控制中的切换控制能够增强被控系统对外界干扰和系统本身不确定性的鲁棒性。

从物理角度看，切换控制的过程就是被控系统状态变量不断趋近于滑模面的运动，因此可以通过切换控制中引入趋近律进而改善趋近运动的动态品质[16]。常用有经典指数趋近律，其数学表达形式如下：

(15)

表达式中：S为滑模面，-kS为指数趋近项，-εsgn(S)为等速趋近项。其中指数趋近项的运动特征是一开始趋近速度比较快，后面趋近速度渐渐缩小到0。当S接近于0时，此时等速趋近项趋近速度为ε，而指数趋近项趋近速度为0，此时由于趋近速度ε的存在，使得系统状态能够在有限的时间内到达滑模面。因此在切换控制中，指数趋近项和等速趋近项这两者缺一不可。然而指数趋近律也有其固有缺点，其中一点是采用指数趋近律，系统状态变量在滑模面来回穿梭形成一个带状的切换带，同时由于系统固有惯性，系统状态无法在滑模面上，只能在滑模面上下做切换运动，这个上下切换运动就是所谓的抖振。由于抖振会激发被控系统中高频成分，这就会影响到滑模控制性能。为此，在系统中引入一种新型指数趋近律并用于滑模切换控制部分，其数学表达式如下：

(16)

其中：sat(S)为饱和函数，用其来替代理想滑动模态中的符号函数sgn(S)。其中Δ称为“边界层”。饱和函数的实质为：在边界层外，采用切换控制；在边界层内，采用线性化反馈控制。采用饱和函数能进一步削弱到达原点前状态变量运动轨迹的抖振。通过在引入被控系统状态变量绝对值|x1|的幂函数，使得系统趋近滑模面的速度与状态变量有关。当被控系统状态变量离滑模面比较远时，即|x1|较大，此时趋近速度由两项组成，分别是变速趋近律ε·sat(S)|x1|α和指数-ηS两种速率叠加而成，因此趋近速度较快。而当被控系统状态变量靠近滑模面时，S趋近0，指数项-ηS基本不起作用，此时变速项ε·sat(S)|x1|α起主要作用，随着切换函数将状态变量拉回滑模面并趋于原点，在这个过程中变速项ε·sat(S)|x1|α由于随着|x1|的不断减小而减小，最终系统状态变量稳定于原点，这样滑模控制中的抖振现象就得到抑制，克服了常规指数趋近律的不足。

通过上面的分析，可以推导出滑模控制的切换控制部分ud的数学表达式如下式所示：

(17)

2.3 滑模控制律的确定

由式(14)和式(17)可知，滑模控制器的控制律函数如下：

(18)

3 系统仿真

基于MATLAB/Simulink建立永磁同步电机驱动纯电动汽车的速度-电流双闭环控制系统的仿真模型如图3所示。

图3 PMSM驱动PEV的调速控制系统的仿真模型Fig.3 The simulation model of speed control system of PEV driven by PMSM

仿真系统的控制对象所采用的主要参数如表1所示。

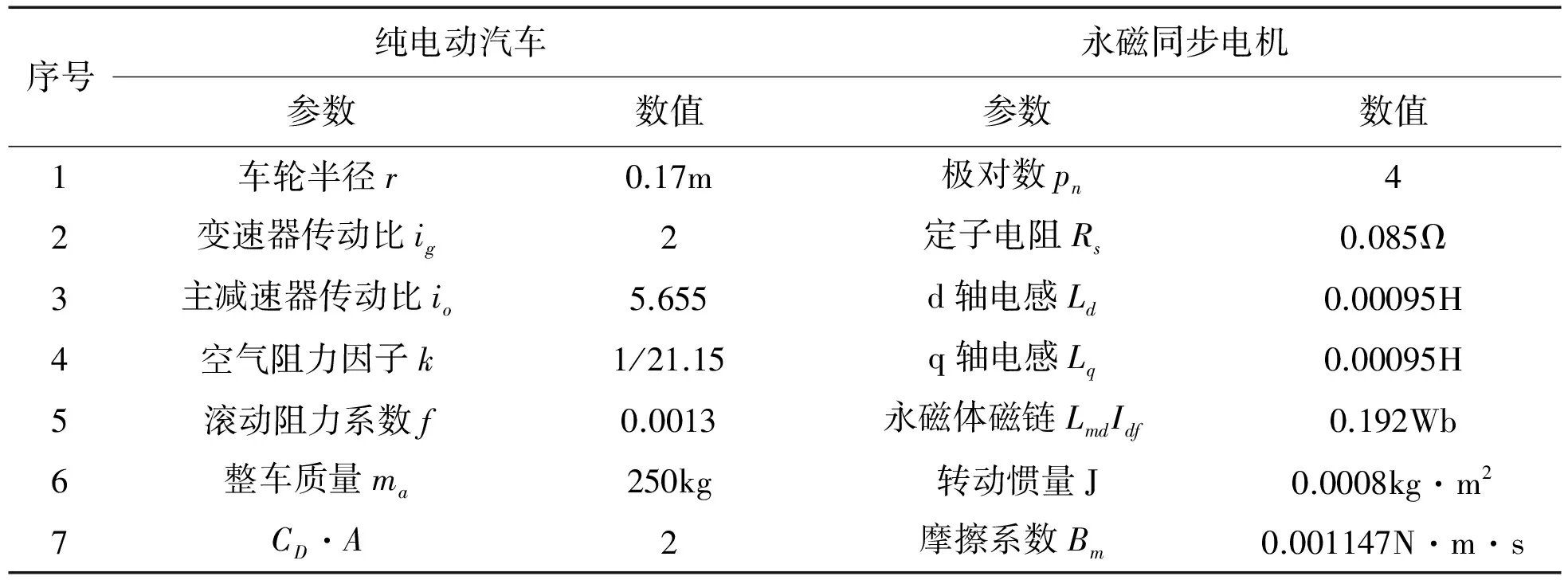
表1 纯电动汽车和永磁同步电机的主要参数

积分滑模控制器所采用的主要参数如下：c=2，α=0.5，k=0.09，ε=0.5，Δ=0.2；PID控制器所采用的主要参数如下：kp=0.2，ki=3，kd=0.01。

为了验证该控制系统的调速跟踪性能，初始给定车速18.15km/h，根据车速与电机输出转速方程(10)，此时需要电机输出转速为1500r/min，接着在0.5s指定车速变为24.2km/h，即电机需输出转速为2000r/min.对上述过程进行仿真，仿真结果如图4、图5所示。

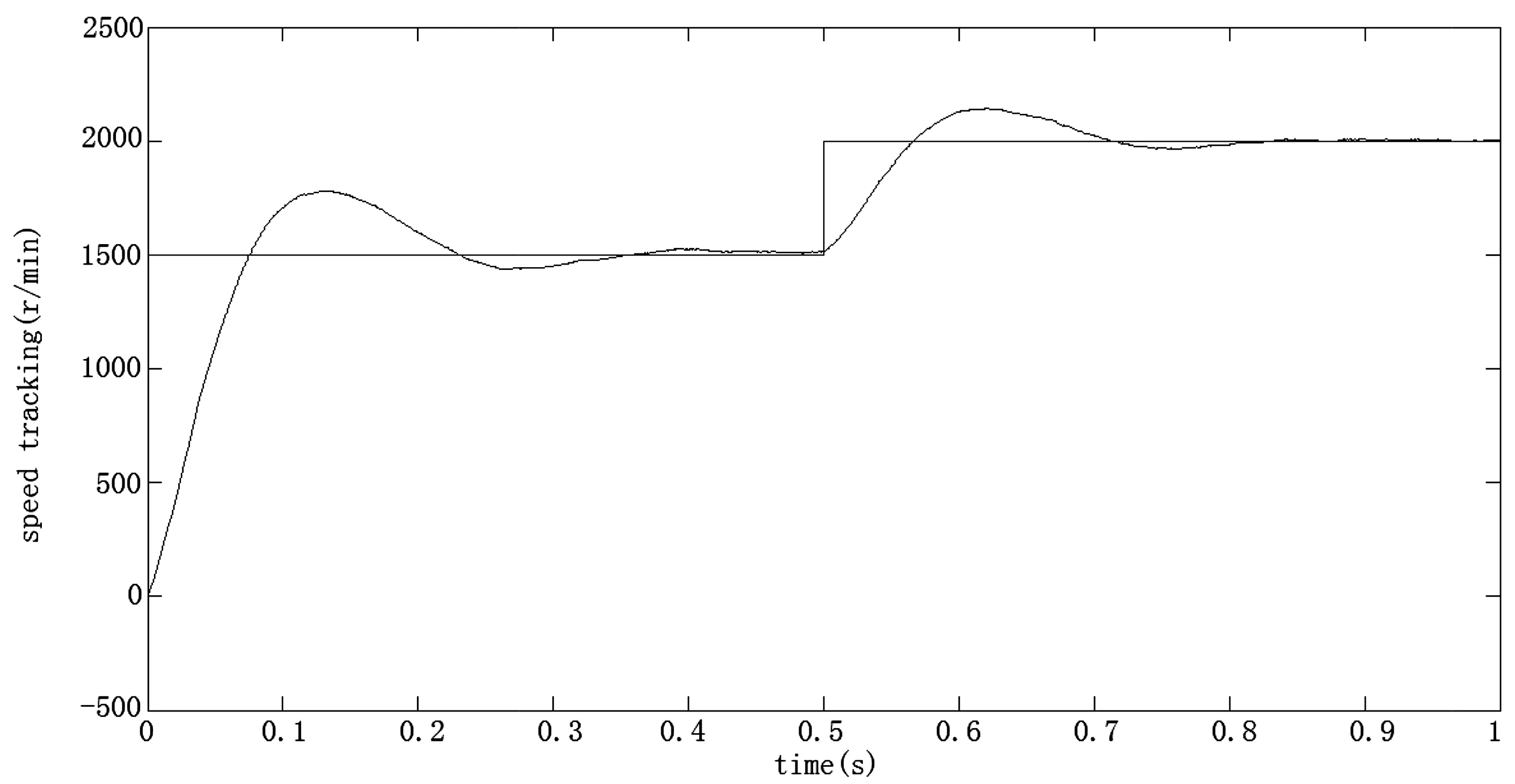
图4 基于传统PID控制器的PMSM输出转速图Fig.4 The speed figure of PMSM based on the traditional PID controller

图5 基于新型积分滑模控制器的PMSM输出转速图Fig.5 The speed figure of PMSM based on the novel SMC controller

仿真结果表明：采用新型积分滑模控制器的PMSM驱动的PEV调速系统相对于采用传统的PID控制器的PMSM驱动的PEV调速系统具有更快的响应速度，系统调整时间更短，超调量更小，稳态误差更小，同时速度追踪响应时间更短。

4 结论

目前电动汽车对其驱动调速系统的要求是运行稳定可靠、调速快，根据这些要求结合PMSM自身特点，将具有增强抗干扰能力的积分滑模控制器应用于被控系统的速度环控制器中，同时提出一种新型的趋近律，有效地抑制了滑模固有的抖振现象；同时在滑模控制方案中提出了一种新型函数切换控制律，并根据误差大小来决定是否引入切换控制，在一定程度上降低了抖振。仿真结果表明，基于新型积分滑模控制器的PMSM驱动的PEV调速控制系统与基于PID控制器的PMSM驱动的PEV调速系统具有更好的动态和稳态性能。

[1]于寅虎.新型电机控制技术用于电动汽车的机遇与挑战[J].电子产品世界，2014，(09)：12-13.

[2]杨竞衡.电动汽车的电气传动系统[J].电气传动，1999，(04)：3-10．

[3]毛亮亮，王旭东.蚁群算法在永磁同步电机起动过程中的应用[J].电力电子技术，2015，49(11)：74-76，80.

[4]黄明明，郭新军，周成虎，等.一种新型电动汽车宽调速驱动系统设计[J].电工技术学报，2013，28(04)：228-233.

[5]顾欣，李珂，张承慧，等.电机大范围调速的综合电压调制策略[J].电气传动，2016，46(05)：12-15.

[6]佘致廷，卢文斗，谭琼琼，等.PMSM神经网络模型参考自适应的速度控制[J].控制工程，2015，22(S1)：29-34.

[7]王巍.基于分数阶PID控制的永磁直驱电机仿真研究[J].电测与仪表，2016，53(S1)：223-226.

[8]全龙虎，王继东，崔赫日，等.基于PSO的PMSM模糊PI速度控制器设计[J].控制工程，2016，23(05)：629-635.

[9]胡佳琳，秦哲，臧怀泉，等.电动汽车永磁同步电机遗传优化鲁棒控制[J].燕山大学学报，2017，41(01)：51-55.

[10]赵志刚，沈洋.基于SDRE的PMSM调速系统非线性控制[J].微特电机，2014，42(12)：49-53.

[11]刘金琨，孙富春．滑模变结构控制理论及其算法研究[J].控制理论与应用，2007，24(03)：407-418．

[12]LIN F J，SHEN P H.Robust Fuzzy Neural Network Sliding-Mode Control for Two-Axis Motion Control System[J].IEEE Transactions on Industrial Electronics，2006，53(04)：1209-1225.

[13]于志生.汽车理论[M].北京：机械工业出版社，1989.

[14]汪贵平，马建，杨盼盼，等，电动汽车起步加速过程的动力学建模与仿真[J].长安大学学报(自然科学版)，2009，29(06)：98-102.

[15]刘金琨，滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005：24-25.

[16]刘金琨，孙富春．滑模变结构控制理论及其算法研究与进展[J]．控制理论与应用，2007，24(03)：407-418．