由一道高考题引发的思维风暴
陕西省靖边中学(718500) 赵世念
“问题是数学的心脏.”一个好的问题可以点燃学生的思维火焰,犹如一块石头投入平静的思维海洋,激起层层思维波澜,问题不止,思考不断.一道好的试题可以激发教师的探究欲望,一旦教师的思维被激活,奇思妙想仿佛“千树万树梨花开”,种种问题源源不绝.2014年高考广东省理科试卷第20题就是这样的好题.解完此题,让笔者浮想联翩,神游古今,学语前辈,草就此文.
一.试题再现与推广
(1)求椭圆C的标准方程;
(2)若动点P(x0,y0)为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程.

9,4,13这组数是偶然,还是必然?可否形成一般结论?
则动点P的轨迹为圆x2+y2=a2+b2.
证明 设两切线为l1,l2,点P的坐标(x0,y0).
(1)当l1⊥x轴或l1//x轴时,对应l2//x轴或l2⊥x轴,可知P(±a,±b).
(2)当l1与x轴不垂直且不平行时,x0/=±a.设l1的斜率为k,则k/=0,l2的斜率为
由上可得l1的方程为y-y0=k(x-x0),其与椭圆方程=1联立,消去y得

因为直线l1与椭圆C相切,所以∆=0,即

所以k是方程

二.思维风暴
爱因斯坦曾说过:“解决问题好比在草堆中寻针.别人往往寻找到一根针时即停止不再费力去做了,但我自己却会遍寻干草堆中的所有藏针,不达目的决不罢手.”题干中涉及曲线的形状—椭圆,两条直线的夹角—,动点的位置—椭圆外,倘若我们变换曲线形状、改换夹角范围、更换动点位置,所求轨迹会发生什么变化呢?
风暴1 变换曲线形状
二次曲线的性质往往具有遗传,类比到圆、双曲线和抛物线中考虑问题.
结论2 在平面直角坐标系中,过点P作圆x2+y2=r2(r>0)的两条切线,切点分别为A、B,若∠APB=,则动点P的轨迹为圆x2+y2=2r2.
结论4 在平面直角坐标系中,过点P作抛物线y2=2px(p> 0)的两条切线,切点分别为 A、B,若
风暴2 改换夹角大小
结论5 在平面直角坐标系中,过点P作圆x2+y2=r2(r> 0)的两条切线,切点分别为A、B,若∠APB= θ(0<θ<π),则动点P的轨迹方程为(x2+y2)(1-cosθ)=2r2(r>0).


若两切线中有一条无斜率,则点P的坐标为

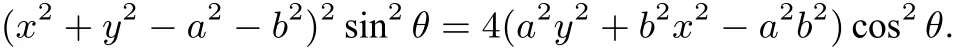
结论8 在平面直角坐标系中,过点P作抛物线y2=2px(p> 0)的两条切线,切点分别为 A、B,若∠APB= θ(0< θ< π),则动点 P的轨迹方程为(2x+p)2sin2θ =4(y2-2px)cos2θ.
风暴3 更换动点位置
我们发现上述八个结论中所涉及动点P的位置均在曲线外部,若将动点P的位置移在曲线内部,当然作不出曲线的切线,但是我们可以利用曲线的中心O做文章.一般孕育在特殊之中,我们先研究垂直情况,再推广到一般.

为了得到结论10的简捷证法,我们先介绍一个引理.
证明 以原点为极点,Ox轴为极轴建立极坐标系,则椭圆方程可化为:
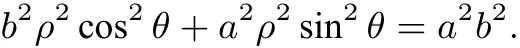
12A、B 均在椭圆上,所以

利用引理证明上述结论就很简单了.
由等面积法得,

结论12 在平面直角坐标系中,过点P作以O为顶点的抛物线y2=2px(p>0)的一条弦,交抛物线于A、则动点P的轨迹为圆(x-p)2+y2=p2.
结论13 在平面直角坐标系中,过点P作以O为圆心的圆x2+y2=r2(r>0)的一条弦,交圆于A、B两点,若OP⊥AB,∠AOB=θ(0<θ<π),则动点P的轨迹方程为2(x2+y2)=(1+cosθ)r2.



故k1、k2是(**)方程的两根.所以
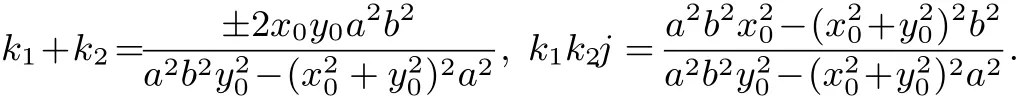
则

即

若两直线中有一条无斜率,则可验证点P的坐标仍适合方程○2;时也适合方程○2.故以x、y代换○2中的x0、y0,即动点P的轨迹方程为
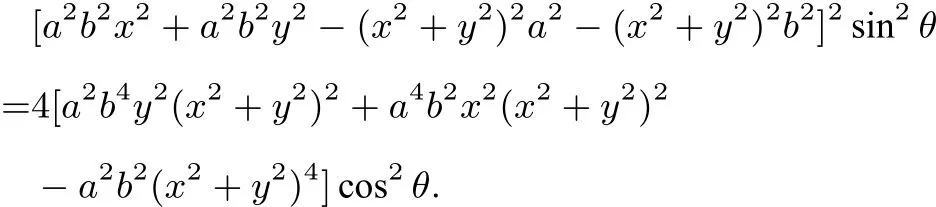
笔者只对部分结论给出了证明,其它结论的证明,要么简单,要么可以模仿,请读者自行推理.下面再给出两个猜想:
[-a2b2x2-a2b2y2-(x2+y2)2a2+(x2+y2)2b2]2sin2θ=4[a2b4y2(x2+y2)2-a4b2x2(x2+y2)2+a2b2(x2+y2)4]cos2θ.
猜想2 在平面直角坐标系中,过点P作以O为顶点的抛物线y2=2px(p>0)的一条弦,交抛物线于A、B两点,若OP⊥AB,∠AOB=θ(0<θ<π),则动点P的轨迹方程为(x2+y2-2px)2sin2θ=4(p2y2+2p2x3+2pxy2)cos2θ.

