基于综合相对交叉熵的多属性群决策方法*

梅孔椿， 马 强， 毛军军，2， 邹 斌

(1.安徽大学 数学科学学院，合肥 230601；2.安徽大学 计算机智能与信号处理教育部重点实验室，合肥 230039；3.安徽广播电视大学 教育科学学院，合肥 230022)

自1965年Zadeh[1]建立了模糊集理论以来，模糊理论的研究越来越受到人们的重视且广泛应用于各个领域。随着人们对模糊集理论的深入研究以及实际应用的发展需要，传统的模糊集理论已经越来越不能满足人们的发展需要了。Zadeh于1975 年提出了二型模糊集(T2FSs)理论[2]，随着二型模糊集理论[3，4]的提出，它比一型模糊集理论有了更为广泛的应用与发展。比如Mendel & John[5]提出了一个新的表示定理，为分析T2FSs 提供了方便。为了度量一个T2Fs的不确定信息，文献[6]定义了一些关于区间二型模糊集(IT2FSs)的测度，比如质心、基数、方差、偏度等。模糊熵的概念是Zadeh[7]于1968年提出的，熵被看做是一种测度模糊集不确定度的重要工具。文献[8]提出了IT2FSs的熵度量公式来测度模糊集的模糊度。文献[9-12]对熵以及模糊集不确定度等做了深入研究，并提出了犹豫模糊熵的概念来度量模糊集的犹豫度。文献[13]提出了对IT2FSs的不确定性信息测度等。文献[14]提出了IT2FSs的模糊因子，犹豫因子等模糊信息测度，对IT2FSs的发展与应用做出了贡献。

目前，不确定信息量的度量注重研究对象本身的不确定性，未深入研究对象与所处环境中的其他对象的度量测度的交互性和动态化。事实上，针对同一个客观对象，由于不同的其他成员对象，它们的交互信息会存在各种不同的知识获取匹配、推理表达、规则喜好、矛盾排除、模糊度、犹豫度，区间度等。这样不同的交互信息会直接影响研究对象本身的不确定性度量。基于在决策过程中决策者往往只关注模糊集自身的不确定性对决策带来的影响，而通常忽略了模糊集之间的相互不确定性关系对决策所造成的影响。在结合前人对模糊集理论研究成果的基础上，提出了IT2FSs之间的相对交叉熵以及综合相对交叉熵。通过建立IT2FSs的综合相对交叉熵和熵的最优化线性模型，求得最优权重。最后进行实例分析证明该方法的可行性和有效性。

1 基本理论

首先，简单回顾关于T2FSs与IT2FSs的相关概念。

定义1[15]设X是一个非空集合，一个二型模糊集A可以被定义如下：

A={(x，u)，uA(x，u)|x∈X，u∈Jx⊆[0，1]}

(1)

其中，对于任意的x和u，都有0≤μA(x，u)≤1。而且，如果模糊集A中的元素是连续的，那么它可以被定义如下：

(2)

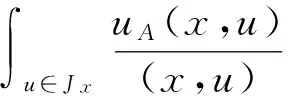
定义2[15]假设A是论域X上的一个二型模糊集，如果对于所有的uA(x，u)=1，那么A就被称为一个IT2FSs，表达形式如下：

(3)

为了方便起见，定义A=(AU，AL)为X上的区间二型梯形模糊集(TIT2Fs) ，故有

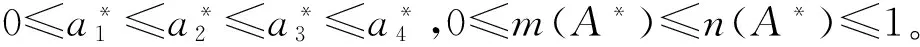
其中 * 代表L或者U， 且AU和AL都表示的是区间一型模糊集，而且满足关系：

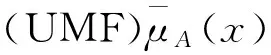
(4)

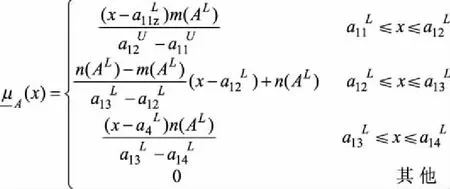
(5)

一般的，对于X上的所有IT2FSs来说，它的补集用AC表示，它的一般表达形式被定义如下：

定义4[16]假设A是一个IT2FSs，算术平均序值公式可以被定义成如下形式：

(6)

该排序值公式由3个部分组成：第一部分反映的是A的平均宽度；第二部分反映的是A的平均高度；第三部分反映的是A的平均长度。

定义5[8]假设A是定义在X上的IT2FSs，且有X=[a，b]，一个实函数E：IT2FSs(A)→[0，1]被称为IT2FSsA的熵。

当A是连续的IT2FSs时，E(A)被定义如下：

(7)

对于X={x1，x2，…，xn} ，式(7)就可以被写成如下的形式：

(8)

它反映的是IT2FSs对自身不确定性的一种度量。

2 IT2FSs的相对交叉熵和综合相对交叉熵

2.1 相对交叉熵

在区间二型模糊环境中度量两个IT2FSs的模糊关系在实际应用中具有十分重要的作用。现提出一种在IT2FSs中的新型相对交叉熵去描述它们不确定信息的识别程度。相对不确定性度量包含3个部分：模糊性、犹豫性和区间性。利用IT2FSs的模糊性、犹豫性和区间性去度量它们之间不确定信息的识别程度。

对任意一个A∈IT2FSs(X)：

定义6

(9)

表示是IT2FSs的模糊因子。其中：

分别表示的是上隶属函数和下隶属函数的模糊性。

定义7

(10)

表示IT2FSs的犹豫因子。其中：

定义8

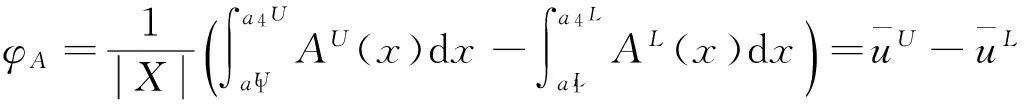
(11)

表示IT2FSs的区间因子。

根据定义，很容易就可以证明δAU，δAL，σAU，σAL∈[0，1/2]，从而有δA，σA∈[0，1/2]以及φA∈[0，1]。更进一步地也可以得到δA=δAC，σA=σAC以及φA=φAC。

定义9 设A，B是两个IT2FSs，且有A，B∈IT2FSs(X)，则A相对于B的交叉熵为

(12)

其中δ，σ，φ分别表示IT2FSs的模糊因子、犹豫因子以及区间因子。

性质1

RE(A，B)=RE(AC，B)=RE(A，BC)=RE(AC，BC)

证明因为前面已经证得δA=δAC，σA=σAC以及φA=φAC，同理可得到δB=δBC，σB=σBC以及φB=φBC，故可以得到RE(A，B)=RE(AC，B)，RE(AC，B)=RE(A，BC)和RE(A，BC)=RE(AC，BC)，因此得到等式关系：

RE(A，B)=RE(AC，B)=RE(A，BC)=RE(AC，BC)

性质2f(δA，σA，φA)是一个实数值的连续函数，且随着δA，σA及φA的增大而增大。

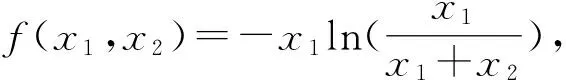
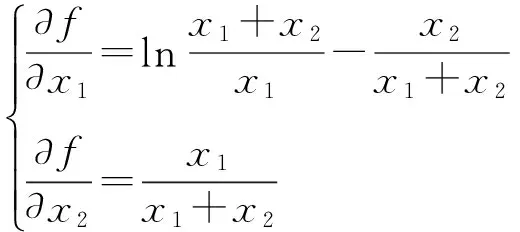
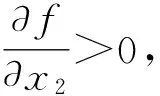
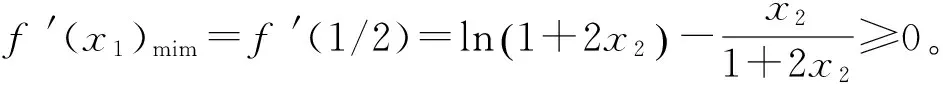
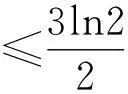
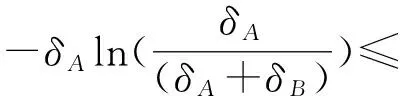
2.2 综合相对交叉熵

本节提出一个新的方法求一个IT2FSs在某一属性下的综合相对交叉熵。在某一属性Cj下，aij相对应akj(i≠k)的交叉熵为RE(aij，akj)，根据相对交叉熵越小越好的公理化准则，在某一属性Cj下，aij相对于akj(i≠k)的RE(aij，akj)越小则应该占aij相对于该属性下其他属性值交叉熵总体有越大的权重。

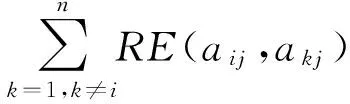
(13)

由式(13)可知，RE(aij，akj)越小，则总体对它的比值t(i，k)就越大。

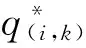
(14)

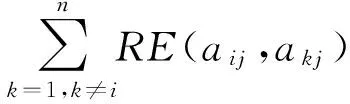
(15)

综上便可以得到在属性Cj下IT2FSsaij的综合相对交叉熵CE(aij)表达式：

(16)

在运用模糊集处理实际问题的过程中，不确定信息量的度量往往注重研究对象本身的不确定性，而未深入研究对象与所处环境中的其他对象的度量测度的交互性和动态化，即往往忽略了模糊集之间存在着相互影响的关系。因此，在不确定信息量的度量中，不仅要考虑模糊集自身的不确定性，同时还要考虑模糊集间的相对不确定性。因此，构造新的二型模糊集不确定信息的度量：

SE(aij) =CE(aij)+E(aij)

(17)

即在对IT2FSs不确定信息量的度量中，不仅要考虑模糊集自身的不确定性，同时还要考虑模糊集之间的相对不确定性。

3 构造综合相对交叉熵和熵的最优化模型求最优权重

由对于一个IT2FSs来说，它的综合相对交叉熵越小越好，同时自身熵的度量也是越小越好。基于上述分析，在属性权重完全未知时，根据最优化原则，建立最优线性规划模型如下：

(18)

构造拉格朗日函数模型：

(19)

其中，λ为参数。求L(wj，λ)对wj和λ的一阶偏导数，并令它们等于零，即：

(20)

求解上述方程组可以得到最优权重：

w=(w1，w2，…，wm)

wj=

(21)

4 决策步骤

提出一种新的基于综合相对交叉熵和熵的多属性群决策方法。

步骤1 计算原始矩阵A=(aij)n×m，将其化为规范矩阵Dk=(dij)n×m，其中

(22)

步骤2 利用IT2FWA算子去集结各决策者的决策矩阵得到综合决策矩阵：

G=(gij)n×m

其中：

(23)

ek表示的是第k个决策者的权重。

步骤3 基于式(17)计算综合决策矩阵G=(gij)n×m中每个综合属性值的综合相对交叉熵CE(gij)n×m。

步骤4 根据定义5计算区间二型模糊熵矩阵E=(E(gij))n×m。

步骤5 构建最优模型并求最优权重向量：

w=(w1,w2,…，wj)

步骤6 利用IT2OWA算子集结各方案的决策信息，得到它们的综合属性值后利用算术平均排序值公式得到对应方案的排序值Ri。

步骤7 按排序值Ri从大到小排序，最大者即为最优方案。

5 实例分析

利用文献[16]的例子进行对比验证。

步骤1 首先将原始决策矩阵进行规范化，因为4个属性都是效益性属性，故不需要规范化，即Dk= (dij)n×m= (aij)n×m。

步骤2 利用IT2FWA算子去集结各决策者的决策矩阵得到综合决策矩阵G=(gij)n×m，其中：

g11=((0.85，0.97，0.97，1；1，1)，(0.87，0.95，0.95，0.95；0.95，0.95))

g12=((0.70，0.85，0.85，0.94；1，1)，(0.74，0.82，0.82，0.91；0.95，0.95))

g13=((0.65，0.85，0.85，0.95；1，1)，(0.7，0.8，0.81，0.87；0.95，0.95))

g14=((0.80，0.96，0.96，1；1，1)，(0.84，0.93，0.93，0.93；0.95，0.95))

g21=((0.61，0.80，0.81，0.93；1，1)，(0.65，0.75，0.76，0.87；0.95，0.95))

g22=((0.68，0.88，0.89，0.97；1，1)，(0.73，0.83，0.84，0.89；0.95，0.95))

g23=((0.85，0.97，0.98，1；1，1)，(0.88，0.95，0.95，0.95；0.95，0.95))

g24=((0.85，0.97，0.98，1；1，1)，(0.88，0.95，0.95，0.95；0.95，0.95))

g31=((0.70，0.86，0.87，0.95；1，1)，(0.74，0.82，0.83，0.91；0.95，0.95))

g32=((0.83，0.92，0.93，0.97；1，1)，(0.85，0.9，0.91，0.96；0.95，0.95))

g33=((0.88，0.96，0.98，1；1，1)，(0.9，0.96，0.97，0.97；0.95，0.95))

g34=((0.59，0.77，0.79，0.92；1，1)，(0.64，0.74，0.75，0.86；0.95，0.95))

g41=((0.74，0.86，0.88，0.95；1，1)，(0.77，0.84，0.85，0.93；0.95，0.95))

g42=((0.68，0.87，0.88，0.97；1，1)，(0.73，0.83，0.85，0.88；0.95，0.95))

g43=((0.70，0.83，0.84，0.94；1，1)，(0.74，0.81，0.83，0.91；0.95，0.95))

g44=((0.77，0.91，0.92，0.97；1，1)，(0.80，0.88，0.89，0.93；0.95，0.95))

步骤3 利用式(16)计算综合决策矩阵G=(gij)n×m中gij的综合相对交叉熵CE(gij)n×m：

(24)

步骤4 通过式(8)计算区间二型模糊熵矩阵E。

(25)

步骤5 构建最优模型并求最优权重向量w=(w1，w2，…，wj)。由式(21)求得最优属性权重为w=(0.251 8，0.271 4，0.237 0，0.239 8)。

步骤6 利用IT2OWA算子[17]集结各方案的决策信息，利用算术平均排序值公式得到对应方案的排序值Ri。

经过计算可以得到方案的排序值为R1=1.611 1，R2=1.612 0，R3=1.573 8，R4=1.543 1。

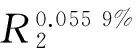
排序顺序与文献[9]是一致的，说明了该方法的可行性。文献[16]在对模糊集不确定性度量中只考虑了模糊集本身的不确定性，而忽略了模糊集之间相对不确定性关系对于决策的影响。笔者定义了新的相对交叉熵和综合相对交叉熵的概念和公式，探究了模糊集之间相对不确定性关系，弥补了文献[16]单纯考虑模糊集自身不确定性的缺点，使决策方法更具系统性和科学性。

6 结 语

在利用模糊集解决实际问题的过程中，大多数决策者往往只关注模糊集自身的不确定性对决策带来的影响，而通常忽略了模糊集之间的相对不确定性关系对决策所造成的影响。基于这种思想，在多属性群决策问题中，提出了IT2FSs之间的相对交叉熵和综合相对交叉熵来度量IT2FSs之间的不确定性关系。基于公理化定义构造综合相对交叉熵和熵的最优线性规划模型，并利用拉格朗日函数法求解最优权重。最后利用IT2FOWA算子对每一方案的各属性值进行集结，利用算术平均排序值公式得到最终各方案的排序值，并用实际例子证明该方法的实用性和有效性。

[1] ZADEH L A.Fuzzy Sets [J].Information and Control，1965，8(3)： 338-353

[2] ZADEH L A.The Concept of a Linguistic Variable and Its Application to Approximate Reasoning[J].Information Science，1975，8(3)： 199-249

[3] 胡宝清.模糊理论基础[M].武汉： 武汉大学出版社，2004： 20-40

HU B Q.Fundamentals of Fuzzy Theory[M].Wuhan：Wuhan University Press，2004： 20-40

[4] NIEWIADOMSKI A.Imprecision Measures for Type-2 Fuzzy Sets：Applications to Linguistic Summarization of Databases [J].Lecture Notes in Artificial Intelligence，2008，5097： 285-294

[5] WU D R，MENDE J M.Uncertainty Measures for Interval Type-2 Fuzzy Sets[J].Information Sciences，2007，177(23)：5378-5393

[6] VLACHOS IK，SERGIADIS GD.Intuitionistic Juzzy Infor-mation-applications to Pattern.Recognition[J].Pattern Recoghi tion Letters,2007,28:197-206

[7] ZADEH L.A，Probability Measures of Fuzzy Events[J].Journal of Mathematical Analysis and Applications,1963(23):421-427

[8] ZENG W，LI H.Relationship between Similarity Measure and Entropy of Interval Valued Fuzzy Sets[J].Fuzzy Sets Syst，2006,157(11):1477-1484

[9] XU Z S，XIA M M，Hesitant Fuzzy Entropy and Cross-entropy and Their Use in Multiattribute Decision-making[J].International Journal of Intelligent Systems，2012(27):799-822

[10] GREENFIELD S.Uncertainty Measurement for the In-terval Type-2 Fuzzy Set，International Conference on Artificial Intelligence and Soft Computing[M].Springer International Publishing，2016

[11] GREENFIELD S，JOHN R I.The Uncertainty Associated With a Type-2 Fuzzy Set，Views on Fuzzy Sets and Systems from Different Perspectives[M].Springer Berlin Heidelberg，2009

[12] ZHAO N，XU Z S，LIU F J.Uncertainty Measures for Hesitant Fuzzy Information[J].International Journal of Intelligent Systems,2015(30):818-836

[13] ZHAI D Y，MENDEL J M.Uncertainty Measures for General Type-2 Fuzzy Sets[M].Elsevier Sciences，2011

[14] MAO J J，YAO D B，WANG C C.A Novel Cross-entropy and Entropy Measures of IFSs and Their Applications[J].Knowledge-Based Systems,2013,(48:)37-45

[15] MENDEL J M.Type-2 Fuzzy Sets and Systems： an Overview[J].IEEE Intelligence Magazine,2007,2(1):20-29

[16] QIN J D，LIU X W.Multi-attribute Group Decision Making Using Combined Ranking Value under Interval Type-2 Fuzzy Environment[M].Elsevier Sciences，2015

[17] ZHOU S M，JOHN R I，CHICLANA F，et al.On Aggregating Uncertain Information by Type-2 OWA Operators for Soft Decision Making[J].International Journal of Intelligent systems,2010,25(6):540-558