基于锁相环原理的相位噪声优化实践
钱发飞, 傅小明, 罗 丽
(1.紫金县职业技术学校 电子电工科,广东 紫金 517400;2.中兴通讯股份有限公司,深圳 518057)
时钟是通信系统工作的心脏,时钟出现异常,则单板无法正常工作。PLL输出时钟指标主要包含两部分,频率与相噪。通常输出正确的频率很容易做到,但输出高性能的相噪,则有很多工作要做。通信系统的传输带宽越来越高,对相噪的要求也相应地提高。从现有文献来看,文献[1]侧重解决基站时钟杂散指标的优化;文献[2]则重点强调电路板设计师在降低电路板、芯片和单元模块的噪声相位和抖动时,电路设计中应用的相关技术。传统的相位噪声分析方法是通过总的噪声功率与噪声带宽来量化表征PLL的噪声过程,这种方法的缺陷是它无法得到PLL的动态行为,并采用一种新的分析方法,即通过线性叠加的方法分析PLL中噪声的动态行为。现将通过理论分析和实际案例,给出相噪优化的方法。
1 PLL理论基础
锁相是相位同步的自动控制,能够完成两个电信号相位同步的自动控制闭环系统叫做锁相环,简称PLL[3]。锁相环主要由相位检测器(PD)、电流模式的电荷泵、分频器、环路滤波器及压控振荡器(VCO)等部分组成,如图1所示。最简单的锁相环包含有相位检测器、环路滤波器及VCO三部分。
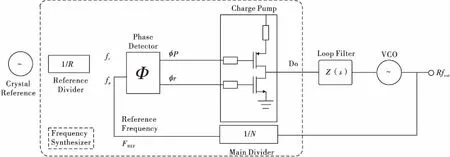
图1锁相环基本结构
Fig.1Basicstructureofphaselockedloop
相位检测用于提取参考信号及VCO反馈信号的相位信息,通过恒流源模式的电荷泵把两个不同相位的信号转化为电流信号,再通过环路滤波器的阻抗网络,把电流信号变换成电压信号,对VCO的输出进行控制。锁相环的基本数学模型如图2所示:
图2中,Kφ表示相位检测常数,是指每弧度的相位差异所产生的电流输出量,它一般由电荷泵的特性来决定。电荷泵鉴相器的S域等效模型为Kφ=Icp/2π,单位为mA/rad。Z(s)是表示环路滤波器的阻抗网络特性的函数。KVCO是表示VCO的压控灵敏度,它表示VCO的输出频率随压控电压的变化,VCO的S域等效模型为KVCO/s,单位为MHz/V。N是VCO的输出频率分频到鉴相所需频率的分频数N= FOUT/FREF[1]。
根据此数学模型,可得到如下关系式。
正向链路增益G(s)为

(1)
反向链路增益H(s)为

(2)
因此可构成一个负反馈系统模型,如图3所示。
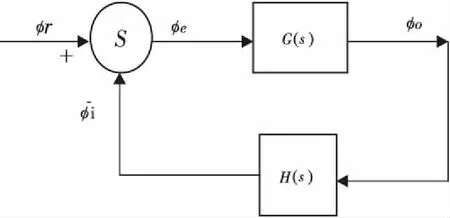
图3 锁相环负反馈模型Fig.3 Negative feedback model of phaselocked loop
由负反馈理论可得,开环传递函数为
G_open(s)=(Kp×KVCO×Z(s))/s
(3)
闭环传递函数为
G_close(s)=G(s)/(1+G(s)H(s))
(4)
开环传输函数中极点的数目称为锁相环的阶数[1]。误差传输函数为
H_e(s)=θ_e(s)/θ_in(s)=1-G_close(s)
(5)
环路带宽定义:开环传递函数幅度等于1时的频率,是环路滤波器设计的关键指标[4]。
2 相位噪声理论分析
2.1 相位噪声定义
相位噪声是在频域范围内,对信号及边带频谱功率的一种度量,如图4所示,用一个频谱信号来解释相位噪声。没有相位噪声时,振荡器的功率都应集中在频率f0处。当出现相位噪声时,振荡器的部分功率将扩展到相邻的频率中去,此时会产生边带[5]。由图4可知,在离中心频率一定距离的偏移频率处,边带功率滚降到1/fm,fm是频率偏离中心频率的差值[2]。
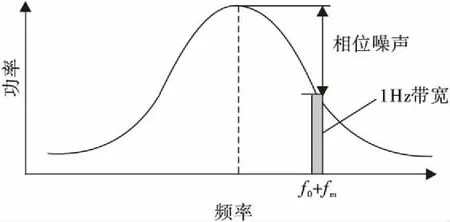
图4 相位波动谱密度Fig.4 Density of phase fluctuation
相位噪声通常定义为在某一给定偏移频率处的dBc/Hz值,其中dBc是以dB为单位的该频率处1 Hz带宽的功率与fo总功率的比值[6]。一个振荡器在某一偏移频率处的相位噪声定义为在该频率处1 Hz带宽内的信号功率与信号的总功率比值[2]。在图4中,用偏移频率fm处1 Hz带宽内的矩形的面积与整个功率谱曲线下包含的面积之比来表示相位噪声,相位噪声约等于中心频率处曲线的高度与fm处曲线的高度之差[2]。该曲线能够反映振荡器相位噪声变化情况和相位波动的谱密度。
2.2 PLL相位噪声模型设计
传统的相位噪声分析,用总的噪声功率与噪声带宽来量化表征PLL的噪声过程,这种方法存在缺陷是无法得到PLL的动态行为。下面将通过线性叠加的方法来分析PLL中的噪声的动态行为。如图5所示,PLL中的噪声和抖动来源于PLL环路中的每个元件,依据功率谱密度(PSD)的线性叠加特性,采用线性叠加的方式来分析总的相位噪声大小。从图5中可以看出主要来源于5部分:Φin(输入参考时钟的相位噪声)、In( 鉴相器和电荷泵的输出等效电流噪声)、Vn(环路滤波器的输出等效电压噪声)、Φn(VCO的输出等效相位噪声)、Φd(分频器的输出等效相位噪声)。Φo表示最终的频率综合器输出信号的相位噪声。
最终输出的相位总噪声是每个模块的相位噪声之和,其关系式为
So(f)=Sref,n(f)|HR(f)|2+Si,n(f)|Hi(f)|2+
Sv,n(f)|Hv(f)|2+Svco,n(f)|Hn(f)|2+
Sd,n(f)|Hd(f)|2
(6)
So(f)(输出的总的相位噪声)主要由5部分相加组成:Sref,n(f)|HR(f)|2为参考源分量的相位噪声,Si,n(f)|Hi(f)|2为鉴相器与电荷泵分量的相位噪声,Sv,n(f)|Hv(f)|2为环路滤波器分量的相位噪声,Svco,n(f)|Hn(f)|2为内部VCO分量的相位噪声,Sd,n(f)|Hd(f)|2为分频器分量的相位噪声。每部分由两项相加构成:其中一项为S(f),表示各模块的相位噪声模型;另外一项为H(f),表示该项相对应的传递函数。
由式(1),推得各项的传递函数数学表达式如式(7),参考源与分频器的传递函数为
(7)
由于G(s)为低通滤波器,可以得到HR(s)的通带模型如下:
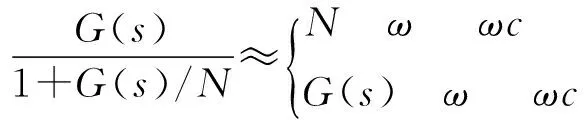
(8)
从式(8)可以看出,HR(s)呈现低通滤波器特性。
电荷泵鉴相器的传递函数为
(9)
环路滤波器的传递函数为
(10)
VCO的传递函数为
(11)
(12)
从式(12)可以看出,HVCO呈现高通滤波器特性。
2.3 各模块相位噪声模型分析
(1) 电荷泵等效输出相位噪声。采样等效噪声模型如图6所示。

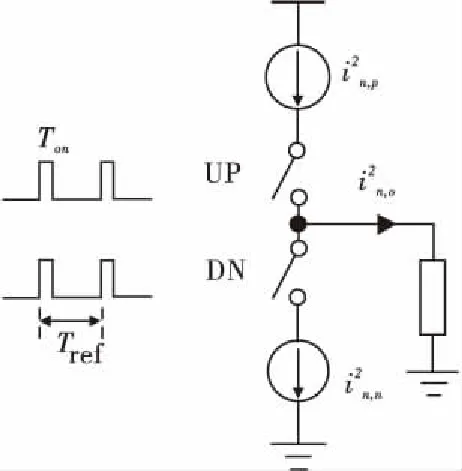
Fig.6Samplingequivalentnoisemodel
锁定时,电荷泵输出的是采样过程,因此采用采样原理对其进行分析:
(13)
由于两项Sin1,Sin2原理相同,因此只对其中一项原理进行分析。依据傅里叶变换,时域相乘相当于频域卷积,可以得到:
Sin1(f)=Sin,p(f)*SUP(f)
(14)
(15)
(16)
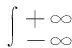
(17)
从表达式(17)可以得出:鉴相频率fref越大,Sin1f越小,因此提高鉴相频率可以减小相位噪声。
(2) 电荷泵电流Icp对输出电流噪声的影响。电流源噪声(主要是MOS管噪声)包含两部分,Si,thermo(热噪声)与Si,flicker(闪烁噪声);
(18)
(19)
结论:等效输出电流噪声与电荷泵电流Icp成正比;电荷泵对环路输出相位噪声的贡献与电荷泵电流Icp成反比[7]。
(3) 环路滤波器等效输出相位噪声。典型的二阶无源环路滤波模型如图7所示。
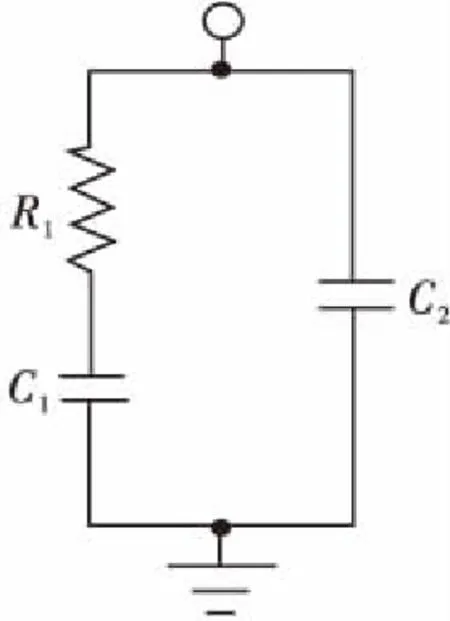
图7 典型的二阶无源滤波器模型Fig.7 Typical passive filter of the two order
环路滤波器的阻抗表示如下:
(20)
ωz和ωp分别是开环传递函数的零点和极点,b=C1/C2是电容比;ωz=1/R1C1;
(21)
开环传递函数为
(22)
其中开环增益:
(23)
二阶无源锁相环环路滤波器的相位噪声函数如下:

(24)
(4) VCO等效输出相位噪声。VCO的相位噪声模型如图8所示,近似分成3段1/f3,1/f2,噪声基底;
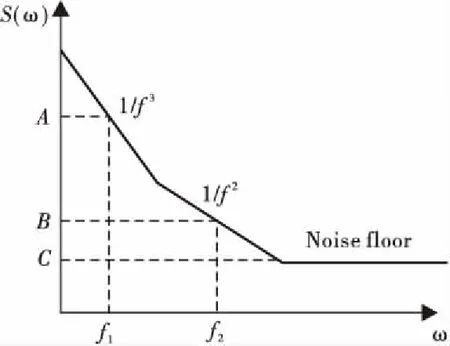
图8 VCO相位噪声数学模型Fig.8 Mathematical model of VCO phase noise
VCO的相位噪声函数如下:
(25)
当f1=10 kHz,f2=1 MHz,A=-89 dBc/Hz,B=-135 dBc/Hz,C=-165 dBc/Hz。VCO相位噪声曲线如图9所示。
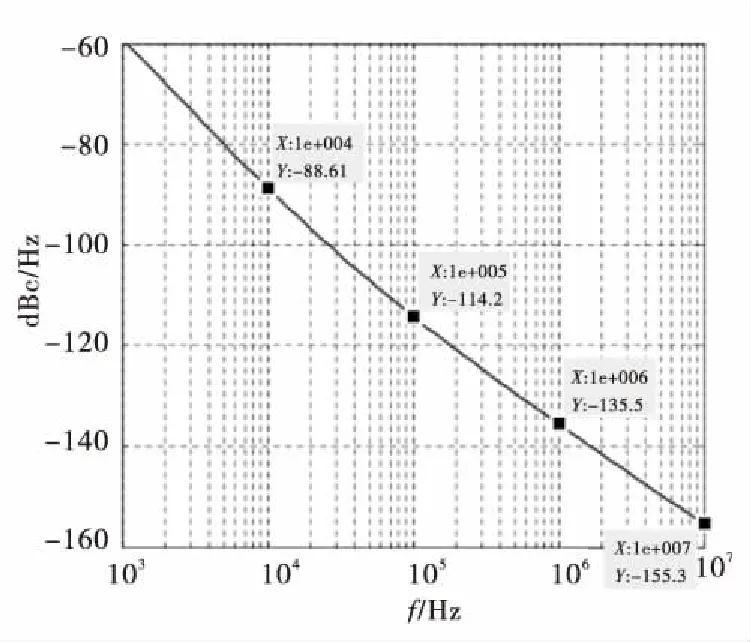
图9 VCO相位噪声曲线示例Fig.9 Example of VCO phase noise curve
(5) 分频器等效输出相位噪声。分频器噪声模型如图10,1/f噪声基底:
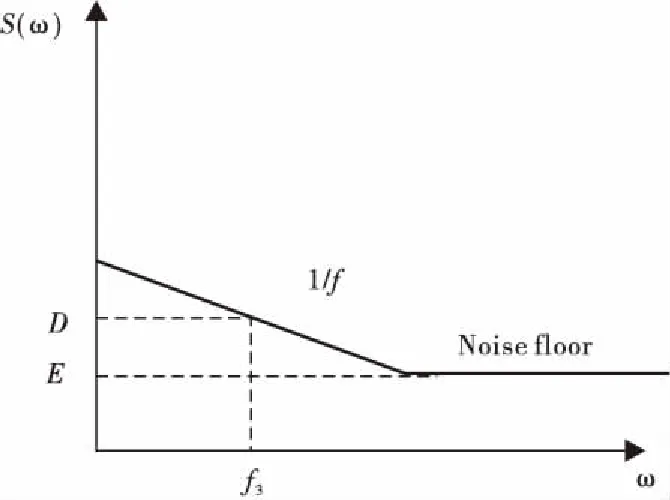
图10 分频器相位噪声数学模型Fig.10 Mathematical model of phase noise
(26)
当f3=10 kHz,D=-150 dBc/Hz,E=-163 dbc/Hz时,相位噪声曲线图11所示。
综合以上分析,降低各模块相位噪声总结如下:
① 电荷泵:增加电路Icp,降低电荷泵锁定导通时间Ton;
② 滤波器:无源,增加电荷泵电流Icp,降低电阻R;有源,降低运放的噪声;
③ 传输函数:采用最优的环路带宽ω;
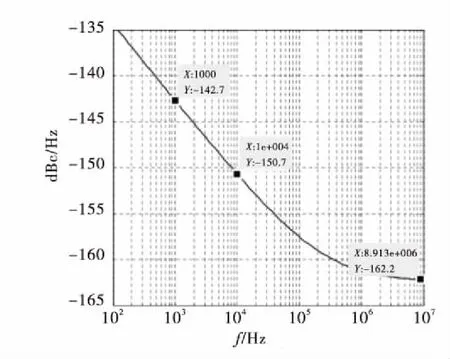
图11 分频器相位噪声曲线示例Fig.11 Frequency divider phase noise curve
④ VCO:降低KV,采用低噪声电路结构,全差分调谐,二次谐波提高阻抗;
⑤ 分频器:降低N,高频时钟同步降低分频器信号的抖动。
3 相位噪声实验与评价
3.1 LMK04806 PLL参数仿真分析
LMK04806是TI公司的一款非常优秀的PLL器件,具有集成度高,相位噪声低等特点,在无线通信系统中大量使用。
为了说明各模块噪声对该器件总的噪声影响大小,采用对比仿真的方式来进行分析,即在相同条件下,只更改一个参数,其他参数不变的情况下进行分析。下面主要对相位噪声仿真中主要的3个参数:环路带宽、电荷泵电流、鉴相频率进行分析。为了更好的说明参数影响,采用LMK04806的第二级锁相环PLL2仿真参数进行仿真分析,参考源VCXO输出相位噪声采用标准的相位噪声模型,内部VCO采用TI公司提供的相位噪声模型,参考源频率20 M,VCO中心频率2 500 M。
通过对比仿真,得到仿真参数数据如表1所示,表格中第1列代表仿真参数的设置,PD为鉴相频率,LP为环路带宽,CP为电荷泵电流。第2列代表参考源(REF_VCXO)相位噪声的大小,第3列代表鉴相器(PLL)相位噪声的大小,第4列代表环路滤波器(LP)的相位噪声大小,第5列代表压控振荡器VCO的相位噪声大小,第6列代表总(ALL)的相位噪声大小。从表1中可以看出,总的噪声并不等于所有噪声相加之和,因为要减去重复相加的底噪。
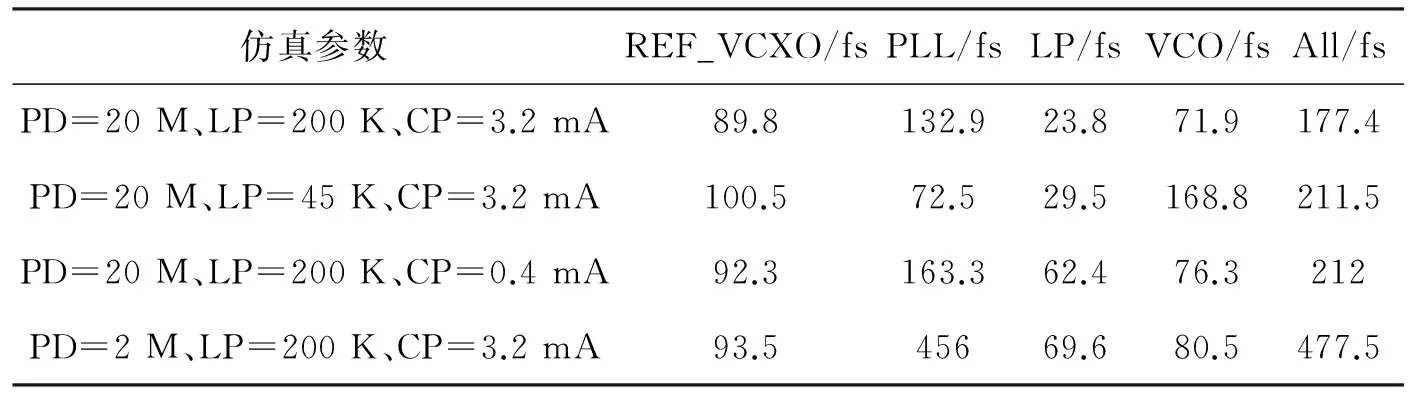
表1 对比仿真数据结果Table 1 Comparison of simulation results
从表1对比仿真结果可以得出:
(1) 相同条件,参考源质量较好的情况下,增大环路带宽有利于减小总的相位噪声。参考源的相位噪声与VCO的相位噪声是互斥的,增大环路带宽,滤掉了VCO的相位噪声,但通过了参考源与鉴相器的相位噪声,环路带宽为200 K的相位噪声177.4 fs小于45 K的相位噪声211.5 fs。
(2) 增大鉴相频率,相位噪声明显减小。相同条件下,鉴相频率为20 M的鉴相器的相位噪声177.4 fs,明显小于鉴相频率为2 M的鉴相器的相位噪声477.5 fs。在提高鉴相频率的同时,还有另一方面的杂散噪声因素需要考虑,它正比于鉴相频率。因此,增加鉴相频率优化了相位噪声,但同时带来了更大的杂散噪声,需要根据具体的PLL芯片来决定提高鉴相频率到什么程度。
(3) 增加电荷泵电流有利于优化相位噪声。从仿真参数可以得出,增加电荷泵电流虽然增加了鉴相器模块的相位噪声,但总的相位噪声减小了。
(4) 减小无源滤波电路中的电阻有利于减小相位噪声。
3.2 典型案例分析
案例故障现象:某单板和其他单板对接时,传输丢包现象严重。传输芯片使用的参考时钟由PLL提供,而PLL器件输出时钟频率正常。通过测试输出的时钟相位噪声,测试波形中显示输出时钟相位噪声指标较差,换算成抖动指标为Rms jitter=134 ps。
PLL输入参考的时钟相位噪声分析:从输入参考的相位噪声频率来看,100 K附近的相位噪声过大,出现一个尖峰。而PLL的环路滤波器基本上没有把这段输出频率的相位噪声减小,导致输出时钟相位噪声质量很差。因此通过优化环路带宽,环路带宽设计远小于100 K,将这一段频率相位噪声衰减掉,来提高输出频率的总相位噪声。
将环路带宽从75 K改到8 K之后,相位噪声换算成抖动的RMS jitter值从134.459 ps锐减到2.374 ps,时钟抖动明显改善,故障消失。和其他单板对接传输一切正常,无丢包现象。
4 总 结
对相位噪声原理从数学角度进行了分析,分析了PLL各模块的相位噪声模型以及各模块相位噪声对总的相位噪声贡献。结合相位噪声仿真软件,对各模块的相位噪声参数设置进行了分析,通过仿真数据来说明各参数对总的相位噪声影响大小。通过对原理的分析,可以更清楚地认识了相位噪声仿真软件各参数的设置,为今后实际工作中如何去优化相位噪声提供了更清晰的思路。
[1] 王雪松,傅小明.无线基站时钟链路杂散指标优化[J].无线互联科技,2015(8):27-29,32
WANG X S ,FU X M.Stray Index Optimization of Wireless Base Station Clock Link [J].Wireless Internet Technology,2015(8): 27-29,32
[2] 覃朝坚,黄敏.低相位噪声信号光纤传输系统的研究与实现方案[J].光通信技术,2007(2):62-63
QIN C J,HUANG M.Research and Implementation of Low Phase Noise Signal Fiber Transmission System [J].Optical Communication Technology,2007 (2): 62-63
[3] 刘小春,樊晓平.锁相环技术在恒压供水同步切换中的应用[J].自动化技术与应,2008(2):111-112
LIU X C ,FAN X P.Application of Phase Locked Loop Technology in Constant Pressure Water Supply Synchronous Switching [J].Automation Technology and Application,2008(2):111-112
[4] 徐金平.X波段小步进频率合成器研究[D].南京:东南大学,2011
XU J P.X Band Frequency Synthesizer With Small Step Research [D].Nanjing: Southeast University,2011
[5] 饶维克.晶体振荡器的无源抗振研究[D].成都:电子科技大学,2011
RAO W K.Research on Passive Vibration Suppression of Crystal Oscillator [D].Chengdu: University of Electronic Science and Technology of China,2011
[6] 胡为东.相位噪声的时域测量方法[J].国外电子测量技术,2011(9):9-12
HU W D.Method of Phase Noise Measurement in Time Domain [J].Foreign Electronic Measurement Technology,2011 (9): 9-12
[7] 汪陆浩.全差分电荷泵锁相环的研究与设计[D].江苏镇江:江苏大学,2011
WANG L H.Research and Design of Fully Differential Charge Pump Phase Locked Loop[D].Zhenjiang: Jiangsu University,2011

