随机需求下考虑价格依赖的制造商生产决策研究*

周 继 祥

(重庆工商大学 商务策划学院，重庆 400067)

0 引 言

随着市场竞争全球化趋势加剧，企业生存的不确定性不断加大，使得企业间的竞争十分激烈。越来越多的企业意识到，产品的竞争力并非由单一企业决定，而是由从原材料供应到产品完成的整个过程决定，而产品的竞争也已经演变成供应链之间的竞争。为了在激励竞争的市场环境中取得竞争优势，企业必须与供应链的上、下游企业保持更加紧密的联系，甚至改变传统的合作模式。

订货权是零售商的重要权利。零售商可以通过这一权利的有效执行影响产品的销售价格，从而影响自身利润的实现以及制造商的决策。因此，国内外众多学者从不同角度对零售商订货问题进行了研究。一些学者研究了零售商在随机市场需求情形下的订货问题。如，Petruzzi和Dada[1]分别在“和式”与“积式”需求函数下研究了零售商的订货问题。周艳菊等[2]运用前景理论，针对随机需求条件下的两产品订货问题进行了研究。褚宏睿等[3]在周艳菊等的研究基础上，通过引入回购和缺货惩罚因素分别研究了供应商回购、零售商缺货惩罚以及同时考虑供应商回购和零售商缺货惩罚因素时零售商的订货决策问题。李永飞和苏秦[4]通过返回策略工具，运用Stackelberg非合作博弈理论分别研究了零售商在集中式、分散式决策以及收益共享情形下的订货问题。陈修素[5]在零售商退货和市场需求不确定情形下研究了零售商的订货问题。一些学者研究了零售商资金短缺时的订货问题。张小娟和王勇[6]研究了允许零售商通过仓单质押融资进行二次订购的供应链模型，在二次订购之前，零售商会根据第一次定购量、融资利率等因素决定仓单质押率。占济舟和卢锐[7]研究了零售商受采购资金约束时，供应链采取商业信用和存货质押融资方式时零售商的订货问题。Chen等[8]同时考虑了资金约束和第三方物流企业参与对零售商订货决策的影响。钱佳和骆建文[9]研究了零售商提前支付下的最优订货决策问题。王波等[10]对资金约束下的零售商订货决策问题进行了综述，探讨了已有研究成果存在的局限性，并指出了未来研究方向。一些学者研究了不同风险偏好的零售商订货决策问题。Wu等[11]研究发现当零售商是风险厌恶型决策者时，存库成本对零售商的最优订货决策有着重大的影响。与Wu等的研究不同，Jammernegg和Kischka[12]研究了零售商为风险偏好型的决策者的情形。Han等[13]研究了零售商为风险偏好型以及任意风险厌恶型决策者的情形。还有一些学者研究了通过双渠道销售产品的零售商的订货问题，如Huang等[14]，Hua等[15]。

上述文献研究了零售商在不同环境下的最优订货决策问题。然而，供应链中“牛鞭效应”的客观存在，以及零售商和制造商的竞争关系导致的需求信息不能共享，使得零售商采取最优订货决策时，制造商的最优生产量与市场实际需求量有较大差距。而且，零售商订货将使其独自面对需求风险。为此，零售商将订货权让渡给制造商将有助于企业间的需求信息共享和风险共担，降低“牛鞭效应”带来的不良影响。另外，为了在竞争激烈的市场环境中赢得竞争优势，供应链中的企业也需要创新合作模式，甚至让渡部分权利给上下游企业。如，汪小京等[16]研究了零售商将库存管理的权利让渡给第三方物流企业的TMI模式，王道平等[17]研究了零售商将库存管理的权利让渡给制造商的VMI模式，周继祥和王勇[18]对零售商将采购权让渡给第三方物流的问题进行了研究。现有文献关于零售商将订货权让渡给制造商的研究还很少，只有李富昌[19]在装备制造行业研究了制造商订货的问题。在李富昌[20]研究中，假设需求函数是确定性的。然而，在现实中，由于受到资源或者调查者的预测工具的局限性(Dalrymple，1987)，确切的市场需求信息很难获得，很多时候仅能够预测其分布函数。基于此，本文研究了随机需求信息下零售商将订货权让渡给制造商后对零售商、制造商、供应链的利润以及供应链效率的影响。

1 模型描述和假设

考虑由一个制造商和一个零售商组成的两级供应链。供应链中，销售单一报童产品的零售商面临随机市场需求，需求函数为销售价格p的减函数d(p)。为了增强供应链的竞争力，减轻零售商的需求风险，假设零售商将订货权转让给制造商。即，制造商决定产品的订货数量。由于制造商将按照订货量进行生产活动，因此，本文中订货量和制造商的初次生产量一致。假设，在销售季节开始前，制造商以单位成本c生产q单位产品。在销售季节开始时，若制造商的产量高于实际需求量，零售商将按照实际需求数量采购；若制造商产量不足，制造商将启动紧急生产机制，以单位成本v(v>c)二次生产以补足缺货量。即无论制造商初次生产的数量为多少，零售商将都能够满足市场需求。假设制造商以价格w将产品销售给零售商。在观察到制造商的产品销售价格后，零售商决策其销售价格p。

根据Mills提出的不确定定价理论，假设零售商的需求函数为d(p)=a-bp+ε，其中ε是与价格无关的随机变量，表示随机需求风险。由于本文主要是为了考察零售商将订货权转让给制造商对零售商、制造商以及供应链系统决策和绩效的影响，以及供应链效率的变化，因此，本文将需求函数中的参数a，b标准化为1。令F(ε)和f(ε)分别表示ε的累积分布函数和概率密度函数。令ε的期望E(ε)=0，否则ε的期望可以通过a-bp反映。由于本文主要考虑零售商将订货权转让给制造商后，分散式决策、集中式决策下零售商、制造商和供应链系统绩效的变化，以及供应链效率的变化，因此，本文将零售商需求函数中的参数a和b全部标准化为1。即，零售商的需求函数为d=1-p+ε。同时，假设随机变化ε服从均匀分布，即

α表示风险不确定性的大小。α越大，零售商的需求波动幅度越大，订货面临的风险越大；反之，α越小，零售商的需求波动幅度越小，订货面临的风险越小。

为使模型简单，易于理解，现做如下假设：

(1) 制造商和零售商都是风险中性的，即，他们都是以追求期望利润最大化为目标；

(2) 制造商作为领导者与零售商进行Stackelberg博弈；

(3) 博弈双方具有完全信息。

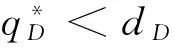
符号说明：p为零售商的销售价格，决策变量；w为产品的批发价格，决策变量；q为制造商第一次生产产品的数量，决策变量；c为制造商第一次生产产品时的成本；v为制造商第二次生产产品时的成本；下标D表示分散式决策的情形，C表示集中式决策的情形。

2 分散决策的情形

2.1 零售商的最优决策

由上述分析可知，零售商的利润函数可以表示为

πR(p)=(p-w)E(d)

(1)

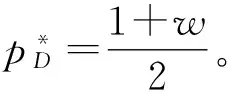
证明将πR(p)对p分别求一阶、二阶倒数可得：

可知，πR(p)是p的凹函数。令其一阶导数为零，求解可得命题1。

由命题可以发现，零售商的最优销售价格与制造商初次生产产品的数量无关。由假设可知，无论制造商初次生产产品的数量为多少，零售商最终都能够且都只采购与实际需求相同数量的产品。因此，制造商初次生产产品的数量对零售商的销售价格不会产生任何影响。

2.2 制造商的最优决策

制造商的利润函数可表示如下：

πM(q，w)=wE(d)-cq-vE[(d-q)+]

(2)

其中，第1项表示制造商将产品销售给零售商获得的收入，第2项表示制造商初次生产的成本，第3项表示制造商第2次生产的成本。

命题2 制造商的最优批发价格和初次最优生产数量可表示如下：

证明将πM(q，w)分别对q，w求一阶、二阶导数和二阶偏导数可得：

(3)

(4)

(5)

(6)

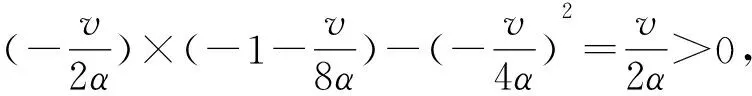
3 集中决策的情形

集中式决策情形下，供应链系统的整体利润等于零售商和制造商的利润之和。集中式决策情形下，供应链系统的期望利润可表示如下

π=pE(d)-cq-vE[(d-q)+]

(7)

其中，第1项为销售收入，第2项为制造商初次生产时的成本，第3项为制造商第2次生产时的成本。

命题3 在集中式决策情形下，供应链系统的最优销售价格和最优初次生产数量可表示如下：

证明过程可参考命题2，此处略去。

4 数值分析

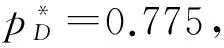
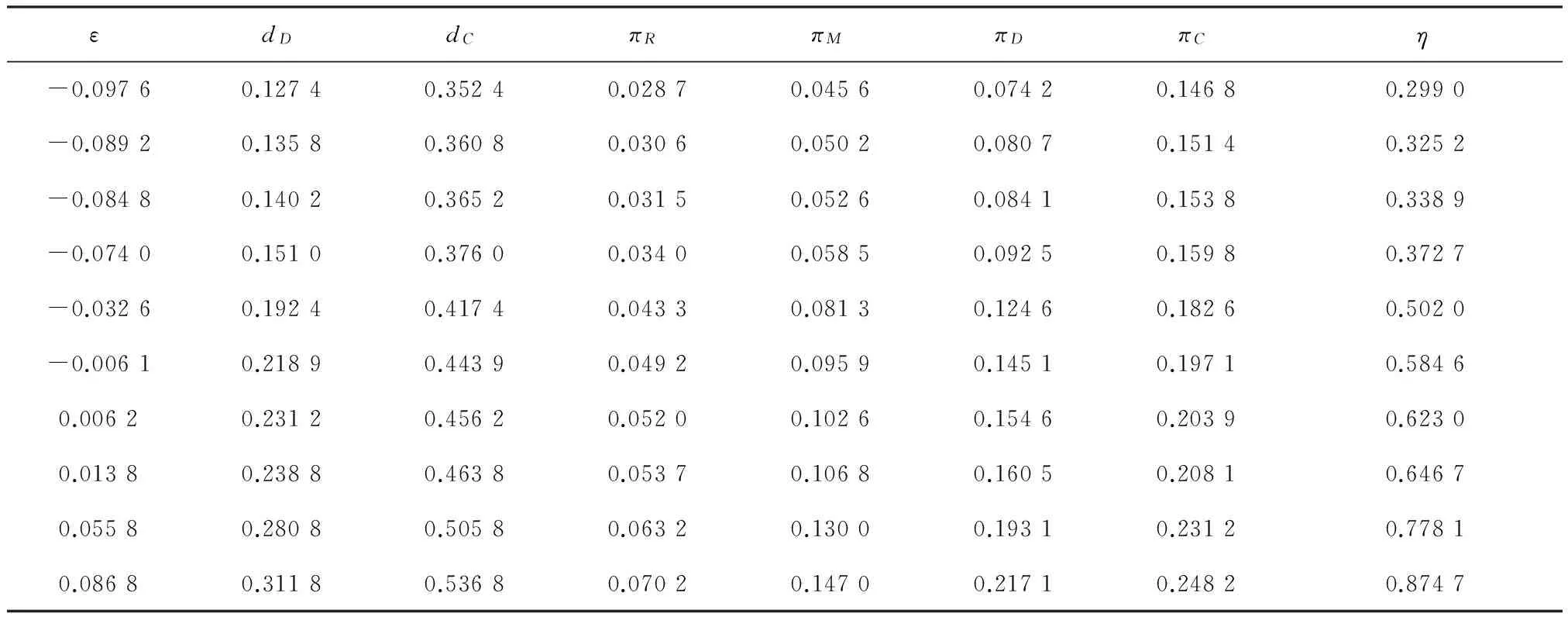
表1 需求风险对需求、利润以及供应链效率的影响Table 1 Impacts of risk on demand and profit and supply chain efficiency

孙彩虹等[21]研究发现，确定性需求情形下线性需求函数的供应链效率为定值75%。分析随机需求下供应链的效率可以发现，当ε>0.055 8时，供应链的效率高于75%。且ε越大，供应链的效率越高。进一步的分析可以发现，当ε在(-0.3,0.3)波动时，分散式决策情形下的供应链利润有可能高于集中式决策情形下供应链的利润。另外，由于集中式决策情形下零售商订货和制造商订货无差别，因此，可以得出一个重要结论：当ε较小时，零售商和制造商应该采取集中式决策以提高供应链利润；而当ε较大时，零售商和制造商应采取分散式决策，即当ε较大时，零售商将订货权转让给制造商可以提高供应链系统的利润。

5 结束语

零售商将订货权让渡给制造商将有助于企业间的需求信息共享和风险共担，降低“牛鞭效应”带来的不良影响。为此，通过建立制造商和零售商的博弈模型研究了随机需求下制造商订货问题。通过上述分析得到以下重要结论：

当需求风险较大时，零售商和制造商采取分散式决策方式可以提高供应链系统的利润，即零售商将订货权转让给制造商可以提高零售商、制造商和供应链系统的竞争力。然而，也有一些不足之处，为了简化模型而假设市场需求服从均匀分布，而没有考虑其他需求分布下零售商、制造商和供应链系统的利润问题，也没有考虑无法得到市场的具体需求分布的情形，这些都是下一步将要研究的内容。

[1] PETRUZZI N C, DADA M. Pricing the Newsvendor Model Problem: A Review with Extensions. Operations Research,1999,47(2):183-194

[2] 周艳菊,应仁仁,陈晓红，等. 基于前景理论的两产品报童的订货模型[J]. 管理科学学报,2013,16(11):17-29

ZHOU Y J, YING R R, CHEN X H, et al. Two-product Newsboy Problem Based on Prospect Theory[J]. Journal of Management Science in China,2013,16(11):17-29

[3] 褚宏睿, 冉伦,张冉，等.基于前景理论的报童问题：考虑回购和缺货惩罚[J].管理科学学报,2015,18(12):47-57

CHU H R, RAN L, ZHANG R, et al. Prospect Theory for Newsvendor Problems: Considering Buyback and Stock-out Penalty[J]. Journal of Management Science in China,2015,18(12):47-57

[4] 李永飞,苏秦.考虑随机需求及返回策略的供应链协调分析[J].软科学,2012,27(2):50-54

LI Y F, SU Q. Supply Chain Coordination with Considering Stochastic Demand and Return Policy[J]. Soft Science, 2012,27(2):50-54

[5] 陈修素.考虑退货价格且需求不确定的易逝品供应链协调性[J]. 重庆工商大学学报(自然科学版), 2008,25(5):470-473,478

CHEN X S. Coordination of Perishable Product’s Supply Chain with Consideration of Return Price[J]. Journal of Chongqing Technology and Business University(Natural Science Edition), 2008,25(5):470-473,478

[6]张小娟,王勇.零售商仓单质押融资二次订购模式下决策与协调[J].系统工程学报, 2015, 30(5):671-681

ZHANF X J, WANG Y. Decision-making and Coordination with Retailer Warehouse Receipts Financing for Second Ordering Mode[J]. Journal of System Engineering, 2015, 30(5):671-681

[7] 占济舟,卢锐.零售商采购资金约束下供应链融资方式的选择策略研究[J]. 管理工程学报,2016,30(3):106-113

ZHAN J Z, LU R. Study on Selection Strategy of Supply Chain Financing Methods with Retailer’s Procurement Capital Constraint[J]. Journal of Industrial Engineering/Engineering Management[J]. 2016,30(3):106-113

[8] CHEN X F, CAI G. Joint Logistics and Financial Services by a 3PL Firm[J]. European Journal of Operational Research, 2011, 214(3):579-587.

[9] 钱佳,骆建文.供应稳定性改善下的零售商提前支付策略[J]. 管理工程学报, 2017, 31(1):79-84

QIAN J, LUO J W. Strategies for Retailer’s Optimal Ad-vance Payment under the Improvement of Supply Reliability[J]. Journal of Industrial Engineering/Engineering Man-agement, 2017, 31(1):79-84

[10] 王波,黄德春,黄正伟. 资金约束供应链融资决策与协调策略研究综述[J]. 重庆工商大学学报(社会科学版), 2016, 33(6):49-55

WANG B, HUANG D C, HUANG Z W. Review of Optimal Decisions-making and Coordination of Strategies of Supply Chain Financing with Capital-constraint[J].Journal of Chongqing Technology and Business University(Social Science Edition), 2016, 33(6):49-55

[11] WU D, BARON O, BERMAN O. Bargaining in Competing Supply Chains with Uncertainty[J]. European Journal of Operational Research, 2009,197(2):548-556

[12] JAMMERNEGG W, KISCHKA P. Risk Preferences and Robust Inventory Decisions[J]. International Journal of Production Economics,2009,18(1):269-274

[13] HAN Q, DU D, ZULUAGA L F. A Risk-and Ambiguity-Averse Extension of the Max-Min Newsvendor Order Formula[J]. Operations Research,2014,62(3):535-542

[14] HUANG S, YANG C, ZHANG X. Pricing and Production Decisions in Dual-channel Supply Chain with Demand Disruptions[J].Computers & Industrial Engineering, 2013,62:70-83

[15] HUA G, WANG S, CHENG T C E. Price and Lead Time Decisions in Dual-channel Supply Chains[J]. European Journal of Operational Research,2010,205:113-126

[16] 汪小京,刘志学,徐娟. 基于系统动力学的第三方物流管理库存模型[J]. 系统管理学报, 2016, 25(2):317-325

WANG X J, LIU Z X, XU J. Third Party Logistics Managed Inventory Model Based on System Dynamics[J]. Journal of Systems & Management, 2016, 25(2):317-325

[17] 王道平, 张博卿, 李小燕. 联合促销下双渠道VMI供应链的竞争与协调[J]. 中国管理科学, 2016, 24(3):52-60

WANG D P, ZHANG B Q, LI X Y. Competing and Coordination Strategies for Dual Channel under VMI Supply Chain with Cooperative Promotion[J]. Chinese Journal of Management Science, 2016, 24(3):52-60

[18] 周继祥, 王勇. 第三方物流参与管理企业采购模型研究[J]. 中国管理科学, 2017, 25(3):121-129

ZHOU J X, WANG Y. Research on the Model of Corporate’s Procurement Management with the Involvement 3PL[J]. Chinese Journal of Management Science, 2017, 25(3):121-129

[19] 李富昌. 具有批发决策权的装备制造商最优决策模型研究[J]. 技术与创新管理, 2017, 38(1):60-63

LI F C. An Optimal Decision Model of Equipment Manu-facturers with the Right of Wholesale Decision-making Power[J]. Technology and Innovation management, 2017, 38(1):60-63

[20] DALRYMPLE D J. Sales Forecasting Practices: Results From a United States Survey[J]. International Journal of Forecasting, 1987, 3: 379-391

[21] 孙彩虹,田真真,于辉.价格需求函数的供应链合作动力对比分析[J].工业工程, 2015,18(4):58-65

SUN C H, TIAN Z Z, YU H. A Comparative Analysis of Supply Chain’s Collaborative Motivation under Different Price-dependent Demand Functions[J]. Industrial Eng-ineering Journal,2015,18(4):58-65