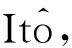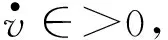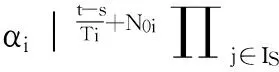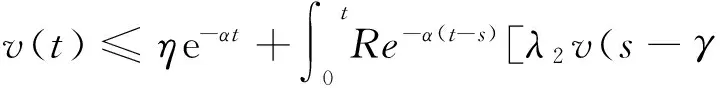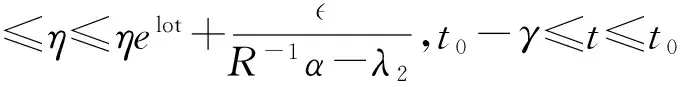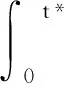具有时变脉冲的随机时滞微分系统的指数稳定性*

李宁宁， 吴小太

(安徽工程大学 数理学院，安徽 芜湖 241000)

0 前 言

随着随机分析理论的飞速发展，随机时滞微分系统已经被广泛应用于机械、电子、控制、物理、金融等众多领域的系统建模与理论分析中，它可以有效地刻画随机因素对系统的影响[1]，并能够反映系统在实际运行过程的时滞现象[2]。同时，脉冲现象在现实世界中广泛存在，如电路系统中开关的闭合，心跳的突然变化，气候突变对生物种群生长的影响，经济学中的一些最优控制等[3-6]。稳定性一直以来都是脉冲随机微分系统性质研究的一个非常重要的研究方向，并已经取得了很多有意义的成果[7-13]。

在脉冲系统中，脉冲可以发挥控制或扰动两种不同的作用。现有文献中大部分将两种情况分开考虑，即分别考虑系统受到控制或扰动脉冲作用时系统稳定的充分条件。然而，在脉冲系统中，这两种类型的脉冲可能会同时出现在一个系统中，即在不同的脉冲时刻发生的脉冲类型不同，它可以随时间推移而发生变化。文献[14]研究了时变脉冲作用下，脉冲神经网络的指数稳定性，使用Lyapunov函数与比较定理的方法，研究了神经网络指数稳定的充分条件。然而，文献[14]中仍然存在着一些局限性，主要体现在以下两个方面：一是在脉冲暂留时间的假定下进行考虑。文献[12-13]提出了平均暂留时间的概念，并说明了平均暂留时间和相对暂留时间有着更加良好的优点，如脉冲的上界可以达到足够大、下界可以充分小；二是文献仅针对确定性脉冲微分系统，而没有考虑系统在随机因素影响下系统的稳定性情况。同时，文献[14]仅针对神经网络考虑了时变脉冲作用下系统的稳定性。

综上所述，本文借助脉冲平均暂留时间的概念，对具有时变脉冲的随机时滞微分系统的稳定性展开研究。借助Lyapunov函数与比较定理的方法，分析在时变脉冲作用下非线性随机时滞微分系统的指数稳定性，并针对不同类型的脉冲分别给出其对应的平均脉冲区间。

1 相关定义

在本文中，将考虑如下具有时变脉冲的随机时滞微分系统：

(1)

其中：

(i)tk,k∈N+是一个严格递增的脉冲时间序列，αk∈R表示脉冲信号的强度。假定I=I∪UIS为所有类型脉冲组成的集合，其中IU={1，2，…，N}为扰动脉冲集合，对∀i∈IU，有脉冲强度│αi│>1；IS={1，2，…，M}为控制脉冲集合，对于∀j∈IS，有脉冲强度│αj│<1。

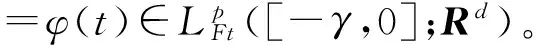
假设C1,2是非负函数V(t,x)在区间[t0-γ,∞)×Rd上的族，其中V(t,x)对于t是一次可微的，对于x是连续两次可微的。 对∀V∈C1,2，针对式(1)，定义算子τV=R+×PC([-γ,0];Rd)→Rd

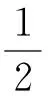
其中：

定义1[1]脉冲随机时滞微分系统式(1)指数稳定，若有

E│x(t)│p

这里M与β均为正常数。

与

则当u(t)≤v(t),-γ≤t≤t0时，有u(t)≤v(t),t≥t0。

2 主要结论

这里将针对具有时变脉冲的随机时滞微分系统式(1)，使用比较定理研究系统指数稳定的充分条件。

定理1 假设存在正常数c1,c2,p,λ2与常数λ1∈R,使得式(H1)-(H4)成立：

(H1)c1│x│p≤V(t,x(t))≤c2│x│p

(H2)EτV(t,x(t))≤λ1EV(t,x(t))+λ2E(t,x(t+θ)),θ∈[-Υ,0]

(H4)α-λ2R>0,这里

则脉冲随机时滞微分系统式(1)指数稳定。

dV(t,x(t))=τV(t,x(t))dt+

Vx(t,x(t))g(t,xt)dB(t)

(2)

因此

EV(t+△t,x(t+△t))-EV(t,x(t))=

(3)

其中△t>0且足够小，使得t+△t∈[tk,tk+1)。故有

D+EV(t,x(t))=EτV(t,x(t))

(4)

于是，由(H2)与(H3)，有

(5)

(6)

这里0≤γ(t)≤t。由引理1，有

EV(t,x(t))≤v(t),t≤0

(7)

易知，方程式(6)的解为

(8)

其中，W(s,t),0≤s≤t是以下微分方程的解：

(9)

由方程式(9)可得到W(s,t)的表达式如下：

W(s,t)=eλ1(t-s)∏s

(10)

对于扰动脉冲i∈IU与控制脉冲j∈IS，由定义2与式(10)可得

W(s,t)=

eλ1(t-s)∏i∈IU│αj│Nj(s,t)∏j∈IS│αj│Nj(s,t)≤eλ1(t-s)

(11)

令η=Rsup-T≤s≤0│φ(s)│，将式(11)代入式(8)，即有：

(12)

定义h(v)=v-α+λ2ReVr。由(H4)可知h(0)<0与h(+∞)=+∞，且h′(v)=1+λ2RγevΥ>0。故存在唯一的β>0使得：

β-α+λ2Reβr=0

(13)

另外，由h(0)<0可知R-1α-λ2>0。因此

(14)

所以，断定

(15)

接下来，将使用反证法证明式(15)。

假设式(15)不成立，那么存在一个t*>0使得：

(16)

以及

(17)

由式(12)和式(17)可得：

(18)

再由式(13)和式(18)可得：

(19)

E│x(t)│p<ηe-βt

(20)

故脉冲随机时滞微分系统式(1)是指数稳定。

[1] Max X.Stochastic Differential Equations and Applications[M].2nd edn.Chichester： Howrwood，2007

[2] KHASMINSKILL R.Stochastic Stability of Differential Eq-

uations[M].Berlin，Heidelberg： Springer-Verlag，2012

[3] AMATO F，TOMMASI G，PIRONTI A.Necessary and Su-fficient Conditions for Finite-time Stability of Impulsive Dynamical Linear Systems[J].Automatica，2013，49(8)： 2546-2550

[4] CHEN W，ZHENG W.Global Exponential Stability of Im-pulsive Neural Networks with Variable Delay： an LMI Approach[J].IEEE Transactions on Circuits and Systems Part I Regular Papers，2006，53(9)： 837-842

[5] CAI S，ZHOU J，XIANG L，et al.Robust Impulsive Sy-nchronization of Complex Delayed Dynamical Networks[J].Physics Letters A，2008，372(30)： 4990-4995

[6] WU X，TANG Y，ZHANG W.Input-to-state Stability of Im-pulsive Stochastic Delayed Systems under Linear Assump-tions[J].Automatica，2016(66)：195-204

[7] WEI W，XIANG X.Optimal Feedback Control for a Class of Nonlinear Impulsive Evolution Equations[J].Computers and Mathematics with Applications，2006，52(5)： 759-768

[8] AHMED N，TEO K，HOU S.Nonlinear Impulsive Systems on Infinite Dimensional Spaces[J].Nonlinear Analysis Theory Methods and Applications，2003，54(5)： 907-925

[9] YANG X，LU J.Finite-Time Synchronization of Coupled Networks with Markovian Topology and Impulsive Effects[J].IEEE Transactions on Automatic Control，2016，61(8)： 2256-2261

[10] YANG Z，XU D.Stability Analysis and Design of Impulsive Control Systems with Time Delay[J].IEEE Transactions on Automatic Control，2007，52(8)： 1448-1454

[11] WU X，TANG Y，ZHANG W.Stability Analysis of Switched Stochastic Neural Networks with Time-varying Delays[J].Neural Networks，2014，51(2)： 39-49

[12] HESPANHA J，LIBERZON D，TEEL A R.Lyapunov Conditions for Input-to-state Stability of impulsive Systems[J].Automatica，2008，44(7)：2735-2744

[13] LU J，HO D，CAO J.A Unified Synchronization Criterion for Impulsive Dynamical Networks[J].Automatica，2010，46，1215-1221

[14] ZHANG W，TANG Y，FANG J，et al.Stability of Delayed Neural Networks with Time-varying Impulses[J].Neural Networks，2012，36(8)： 59-63

[15] 彭薇.时变脉冲耦合神经网络的稳定性分析[J].重庆工商大学学报(自然科学版)，2015，32(8)： 9-13

PENG W.Stability Analysis of Time-varying Pulse Coupled Neural Networks[J].Journal of Chongqing Technology and Business University (Natural Science Edition)，2015，32(8)： 9-13