基于属性关联的犹豫模糊TODIM多属性决策方法*
刘 宁 元
(广东轻工职业技术学院 财贸学院,广州 510000)
0 引 言
自模糊集[1]提出以来,对客观世界各领域的研究从精确集逐渐拓展到了模糊集.作为决策者的主体在现实决策过程中,由于自身的知识背景及思维差异,经常表现出犹豫,认为几个值都有可能,而且彼此很难说服对方,使得最终的决策结果难以达成一致.Torra[2]提出犹豫模糊集,它作为模糊集的一种重要拓展形式,允许用几个可能的值来表示隶属度.目前,基于犹豫模糊信息的多属性决策问题已引起学者们的重视[3-10].
对于多属性决策问题的研究,大多数方法是建立在期望效用理论之上,这些都假设决策者是完全理性的,然而在现实的决策过程中,常常是具有有限理性的心理特征[11].Kahneman和Tversky以“有限理性人”为基础,提出前景理论[12],在考虑决策者心理行为的情形下,对提高多属性决策质量具有重要现实意义[13-19].Gomes和Lima[15]在前景理论的基础上提出TODIM决策方法,重点考虑了决策者的参照依赖和损失规避行为特征.与前景理论有所不同,TODIM方法不需要事先给出决策参考点的信息,通过计算决策者对两两方案比较优势-劣势的感知优势度来解决属性值为清晰数的多属性决策问题.此后,许多学者对TODIM方法进行了深入研究.樊治平等[16]将TODIM方法推广到区间数环境下,利用区间数距离构建方案收益-损失决策矩阵,进而计算方案总体感知优势度并对方案排序.Krohling和Souza[17]将TODIM方法推广到梯形模糊数环境下,提出了一种新的F-TODIM多属性决策方法.Zhang等[6]将TODIM方法推广到犹豫模糊环境下,提出新测度函数进行方案之间优势-劣势比较,进而计算方案的总体感知优势度并对方案排序.Fan等[18]将TODIM方法推广到属性值为清晰数、区间数、语言术语的混合环境下,提出一种混合TODIM多属性决策方法.梁霞[19]将TODIM方法推广到属性值为关联的清晰数环境下,提出属性关联的C-TODIM多属性决策方法.
鉴于现实多属性决策问题中,属性间常存在关联,属性评价结果通常表现出一定程度的犹豫不决,认为几个值都有可能.文献[19]虽然研究了基于属性关联的清晰数TODIM多属性决策方法,但没有涉及不确定的环境下;文献[6]虽然研究了基于犹豫模糊TODIM多属性决策方法,但对于属性间存在关联的情形也没有进行研究.因而研究基于属性关联的犹豫模糊TODIM多属性决策方法具有重要的理论价值和现实意义.为此,针对属性具有关联的犹豫模糊多属性决策问题进行了探讨,通过决策者参照依赖和损失规避心理行为,提出TODIM多属性决策方法,详细给出了该方法的决策过程,并在此基础上进行算例分析.
1 预备知识
1.1 犹豫模糊集的概念
定义1[2]定义在非空集合X={x1,x2,…,xn}上的犹豫模糊集为H={
定义2[8]设h1,h2,h为犹豫模糊数,它们的基本运算法则定义如下:
(1)h1∪h2=H{max(γ1,γ2)|γ1∈h1,γ2∈h2};
(2)h1∩h2=H{min(γ1,γ2)|γ1∈h1,γ2∈h2};
(3)θh=H{(1-(1-γ)θ)|γ∈h}(θ>0);
(4)hθ=H{γθ|γ∈h}(θ>0);
(5)hc=H{(1-γ)|γ∈h}
定义3[6]设犹豫模糊数h=H{γ1,γ2,…,γ#h},犹豫模糊测度函数S(h)定义:
(1)
其中,参数δ(0<δ≤1)是决策者根据实际决策需要给出的一个常数.当δ=1,则式(1)为犹豫模糊数的得分函数[9].对于两个犹豫模糊数h1(x)和h2(x),基于测度函数S(h)排序如下:
若Sδ(h1)>Sδ(h2),则h1优于h2,记h1>h2;
若Sδ(h1)=Sδ(h2),则h1等价于h2,记h1~h2;
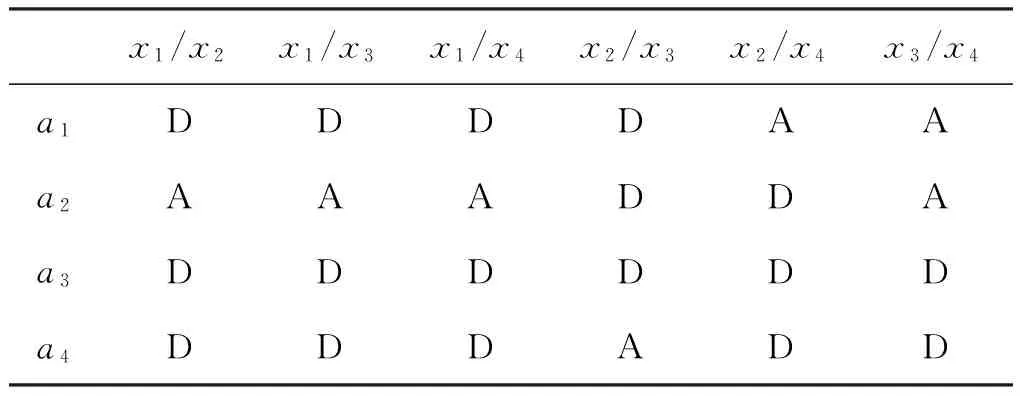
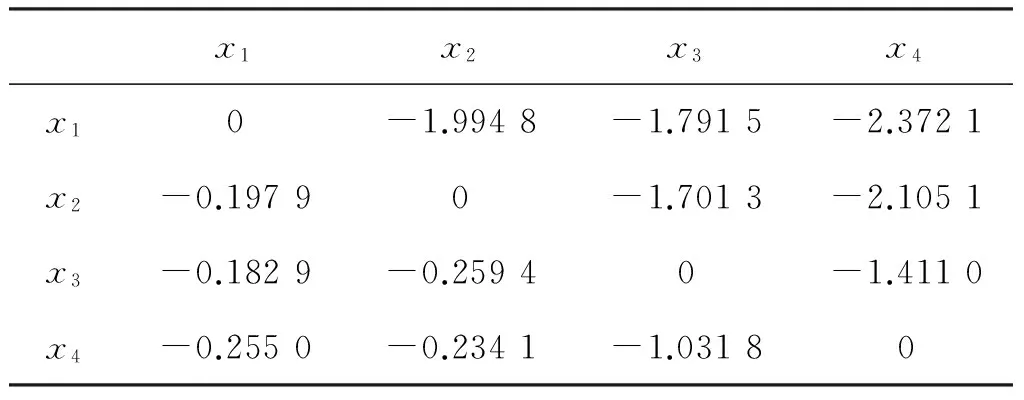
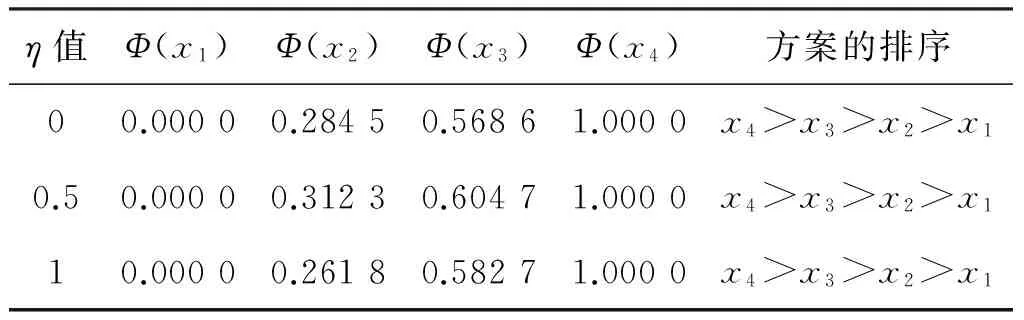
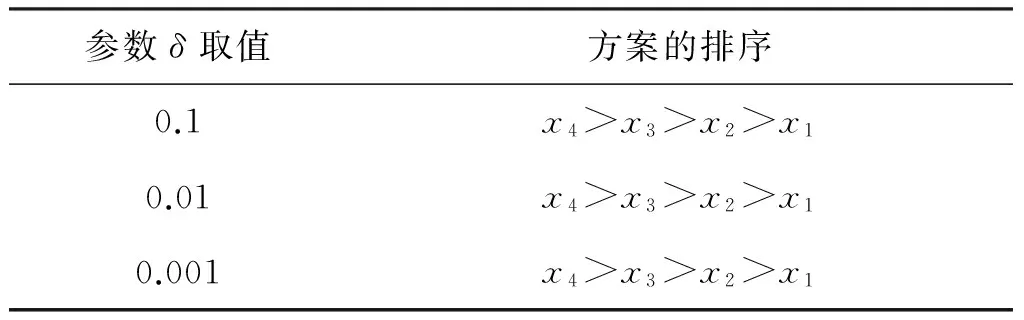
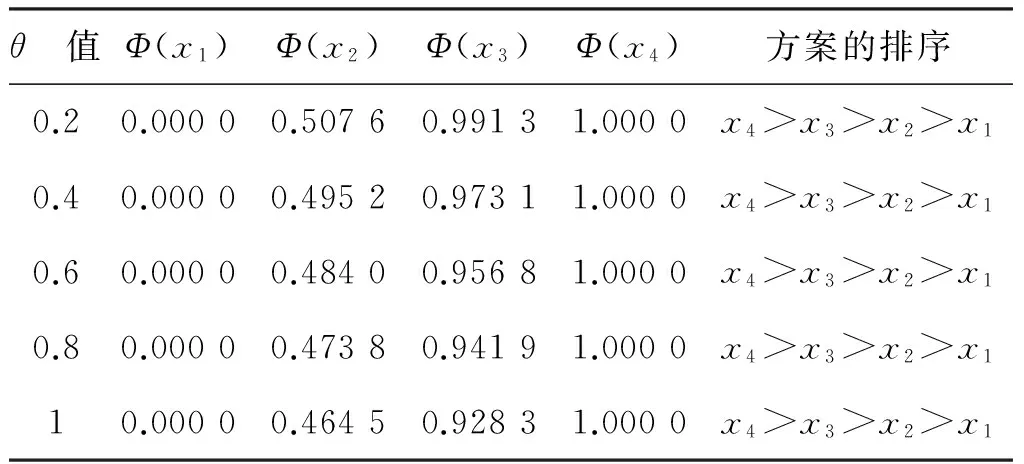
若Sδ(h1) 任意两个犹豫模糊数的元素通常无序,且元素个数也不完全相同.为了进行运算,作如下约定[6]:设犹豫模糊数h1(x)和h2(x)中元素个数分别为#h1和#h2,将h1(x)和h2(x)中元素按照增序进行排列,在元素较少的集合中添加元素,使其个数达到#h=max{#h1,#h2},添加原则反映了决策者的风险态度. 定义4[8]设犹豫模糊数h(x)=H(γλ|λ=1,2,…,#h),设γ-和γ+分别表示h(x)中的最小值和最大值,按照以下方式在h(x)中添加元素: (2) (3) 定义6[20]设X为有限集,P(X)是X的幂集,gλ:P(X)→[0,1]满足性质:(1)gλ(φ)=0,gλ(X)=1;(2)若M⊆N⊆X,则gλ(M)≤gλ(N)≤gλ(X);(3)gλ(M∪N)=gλ(M)+gλ(N)+λgλ(M)gλ(N),其中λ∈(-1,),则称gλ为P(X)上的λ模糊测度. 由定义6可知,当λ=0时,表示gλ是可加测度,M与N间无相互作用关系;当λ>0时,gλ(M∪N)>gλ(M)+gλ(N),表示gλ是超可加测度,M与N间存在积极合作关系;当λ<0时,gλ(M∪N) 如果有限集X={x1,x2,…,xn},对任意的A∈P(X),且gλ模糊测度满足[21]: (4) 因为P(X)=1,根据以下公式,可确定唯一的参数λ: 1+λ=∏i∈A[1+λgλ(xi)] (5) 定义7[22]设f为定义在P(A)上的模糊测度,离散Choquet积分定义为f:A→R+关于μ的映射: (6) 其中(i)表示1,2,…,n的一个置换,满足0≤f(a(1))≤f(a(2))≤…≤f(a(n));X(i)={x(i),…,x(n)},且X(n+1)=φ. 设X={x1,x2,…,xm}表示方案集,A={a1,a2,…,an}表示属性集,μ为定义在P(A)上的模糊测度,方案xi(i=1,2,…,m)在属性aj(j=1,2,…,n)的评价值hij为犹豫模糊数.设H=(hij)m×n是犹豫模糊多属性决策矩阵,其中hij是一个犹豫模糊数,表示方案xi满足属性aj的程度,并且0≤hij≤1.经典TODIM方法[15,23]考虑到决策者损失规避的心理行为特征,计算决策者对两两方案比较的收益-损失值,进而构建在每个属性下的感知优势度矩阵,最后得到各备选方案的总体感知优势度,并以此进行排序择优. (7) φ(xi,xk)= (8) 进一步地,计算方案xi相对于其他方案的总体感知优势度Φ(xi),其计算公式为 Φ(xi)= (9) 显然,0≤Φ(xi)≤1,方案xi(i=1,2,…,m)的总体感知优势度Φ(xi)越大,则方案xi(i=1,2,…,m)就越优. 综上,提出考虑属性关联的犹豫模糊TODIM方法的决策步骤: (10) F1和F2分别表示效益型和成本型属性集.其中(hij)c表示hij补集,按照定义2中式(5)计算. 步骤2 对决策属性A={a1,a2,…,an}的gλ模糊测度进行专家评定,根据式(4)、式(5)确定各属性子集的模糊测度. 步骤4 利用式(8)计算方案xi对于所有属性aj(j=1,2,…,n)下相对于方案xk的个体感知优势度φ(xi,xk). 步骤5 利用式(9)计算方案xi(i=1,2,…,m)总体感知优势度Φ(xi),最后利用总体感知优势度Φ(xi)的大小确定方案xi(i=1,2,…,m)的排序,确定最优决策方案. 定理如果在犹豫模糊信息多属性决策中,决策属性相互独立,则关联的TODIM方法等价于经典的TODIM方法. 证明根据犹豫模糊多属性决策属性关联TODIM方法,方案xi相对于方案xk在所有属性aj(j=1,2,…,n)下集成的感知优势度为φ(xi,xk): φ(xi,xk)= (11) 由于决策矩阵犹豫模糊信息属性相互独立,则属性权重满足可加性,即 μ(Aσ(j))-μ(Aσ(j+1))=μ(a(j)) 将μ(aj)=wj(1≤j≤n)代入式(11),则 (12) 设wjr=wj/wr,其中wr=max{wj|j=1,2,…,n},则 (13) (14) 由式(12)—式(14)可得: (15) 式(15)和文献[6]方法中感知优势度的计算公式是一致的.即决策属性犹豫模糊数相互独立,则关联的TODIM方法等价于经典的TODIM方法. 以文献[24]为例,某企业准备制定未来几年的项目投资计划.假如有4个备选项目需要确定投资重点,董事会利用平衡计分卡评价体系[25]确定了ai(i=1,2,3,4)4个效益型指标:a1财务方向,a2顾客满意方向,a3内部业务流程方向,a4学习成长方向来评估这4个项目的前景,评估结果见表1. 表1 犹豫模糊评估值Table 1 Hesitating fuzzy evaluation value 利用式(7)比较在属性aj(j=1,2,3,4)下两两方案评价值的大小.设δ=0.1,得到表2中所有方案在各个属性下的比较结果.其中“A”表示方案xi/xk比较优势,“D”表示xi/xk比较劣势.例如,在a1财务方向的属性下,决策者认为方案x1要劣于方案x2,因为方案x1在属性a1下的评估值h11为{0.2,0.4,0.7},而方案x2在属性a1下的评估值h12为{0.2,0.4,0.7,0.9}.利用式(1)比较(取δ=0.1)可知,S0.1(h11)=0.387 6 表2 在aj(j=1,2,3,4)属性下方案的优势-劣势比较分析Table 2 Comparative analysis of advantage anddisadvantage under aj(j=1,2,3,4)attribute 由于属性aj(j=1,2,3,4)均为效益型指标,规范化矩阵就是犹豫模糊决策矩阵,见表3. 表3 犹豫模糊决策矩阵D=(hij)4×4Table 3 Hesitation fuzzy decision matrix D=(hij)4×4 步骤2 由专家评定各属性测度gλ值:gλ(a1)=gλ(a3)=0.15,gλ(a2)=gλ(a4)=0.2.利用式(4)、式(5),得到λ=1.4以及所有属性子集的模糊测度,如表4所示: 表4 属性子集的模糊测度Table 4 Fuzzy measure of attribute subset 步骤4 利用式(8)计算方案xi(i=1,2,3,4)在所有属性aj(j=1,2,3,4)下相对于方案xk(k=1,2,3,4)的个体感知优势度φ(xi,xk)取(θ=1),如表5所示. 表5 方案xi(i=1,2,3,4)相对其他方案的个体感知优势度Table 5 The individual perceived advantage of schemexi(i=1,2,3,4) relative to other programs 步骤5 利用式(9)计算方案xi(i=1,2,3,4)总体感知优势度:Φ(x1)=0.000 0,Φ(x2)=0.464 5,Φ(x3)=0.928 3,Φ(x4)=1.000 0. 最后,根据总体感知优势度,得到方案的排序结果为x4>x3>x2>x1. 文献[24]的排序结果为x4>x2>x1>x3,与本文排序有所不同.文献[24]通过犹豫模糊广义λ-Shapley Choquet平均集成算子集成决策信息得到排序结果.信息集成算子是决策者基于完全理性地处理多属性决策的方法,但是在现实生活中决策者往往是有限理性的,因此,提出的方法更加符合现实情况. 由于基于关联的TODIM犹豫模糊多属性决策方法是带有参数η(决策者风险偏好)、参数δ(测度函数S(h))以及参数θ(损失规避系数)的决策方法. 针对决策者不同的风险偏好,参数η取值不同,对原始决策信息中添加的犹豫模糊信息(即属性值)就会发生改变,从而引起犹豫模糊决策矩阵的变化.该敏感分析主要通过改变参数值的大小,分别计算方案最终排序结果的变化情况.参数η分别取0、0.5、1,计算基于η的不同取值下方案排序结果,见表6. 表6 基于η的不同取值下方案排序结果Table 6 The ranking results based on different valuesunder η scheme 从表6中的敏感性分析结果看出,参数η(决策者风险偏好)的值从0变化到1,方案的最终排序结果是一致的.即方案的最终排序结果对参数η的取值不敏感. 针对犹豫模糊测度函数S(h),参数δ取值不同,确定在各属性下方案的优势-劣势比较分析就会发生变化,从而影响方案最终排序.参数δ分别取0.1、0.01、0.001,先进行基于δ不同取值下方案的优势-劣势比较分析,最后计算δ的不同取值下方案排序结果,见表7.这说明参数δ取值对方案排序结果不敏感. 表7 基于δ的不同取值下方案排序结果Table 7 Ranking results based on different values underδ scheme 针对方案感知优势度φ(xi,xk),损失规避参数θ分别为0.2、0.4、0.6、0.8、1,计算基于θ的不同取值下方案排序结果(η=0,σ=0.1),见表8. 表8 基于θ的不同取值下方案排序结果Table 8 Ranking results based on different values underθ scheme 从表8中的敏感性分析结果看出,参数θ的值虽然变化,但方案的最终排序是一致的,这说明参数θ取值对方案排序结果不敏感. 在决策过程中,考虑到决策者行为是有限理性的,这更加符合现实情况.因此,研究考虑决策者“有限理性”的决策问题具有重要的现实意义.针对决策者的属性偏好是犹豫模糊信息,且已知属性关联测度的多属性决策问题,考虑到决策者参照依赖和损失规避心理行为的情形下,提出一种基于TODIM思想的多属性决策方法.该方法通过将其他方案作为参照,引入测度函数对每个属性下方案之间的优势-劣势进行比较,结合TODIM方法和Choquet积分思想,得到方案总体感知优势度,进而对方案进行排序.与已有仅考虑决策者行为且属性关联清晰数的决策方法相比,或与仅考虑决策者行为且属性值为犹豫模糊信息的决策方法相比,所提方法可以有效地处理这两种方法的不足之处.它既考虑到了决策者行为,又考虑到了在不确定的环境下属性间存在着关联的情形,因而具有较强的可操作性和实用性. [1] ZADEH L A.Fuzzysets[J].Information and Control,1965,8(3):338-353 [2] TORRA V.Hesitant Fuzzy Sets[J].International Journal of Intelligent Systems,2010,25:529-539 [3] XU Z S,XIA M M.Distance Measures for Hesitant Fuzzy Sets[J].Information Sciences,2011,181(11):2128-2138 [4] XU Z S,XIA M M.On Distance and Correlation Measures of Hesitant Fuzzy Information[J].International Journal of Intelligent Systems,2011,26(5):410-425 [5] ZHANG Z M.Hesitant Fuzzy Power Aggregation Operators and Their Application to Multiple Attribute Group Ecisionmaking[J].Information Sciences,2013,234:150-181 [6] ZHANG X L,XU Z S.The TODIM Analysis Approach Based on Novel Measured Functions Under Hesitant Fuzzy Environment [J].Knowledge Based Systems,2014,61(1): 48-58 [7] ZHANG X L,XU Z S.Interval Programming Method for Hesitant Fuzzy Muftiattribute Group Decision Making with Incomplete Preference Over Alternatives[J].Computers & Industrial Engineering,2014,75:217-2292 [8] XU Z S,ZHANG X L.Hesitant Fuzzy Multi-attributed-ecision Making based on TOPSIS with Incomplete Weight Information [J].Knowledge Based Systems,2013,52:53-64 [9] XIA M M,XU Z S.Hesitant Fuzzy Information Aggregation in Decision Making[J].International Journal of Approxi-mate Reasoning,2011,52:395-407 [10] 李兰平.犹豫模糊多属性决策M-TOPSIS法[J].重庆工商大学学报(自然科学版),2015,32(6):7-10 LI L P.Hesitation Fuzzy Multiple Attribute Decision Making M-TOPSIS Method [J].Journal of Chongqing Technology and Business University (Natural Science Edition)2015,32(6):7-10 [11] SIMON H A.Administrative Behavior[M].Glencoe: Free Press,1976 [12] KAHNEMAN D ,TVERSKY A.Prospect Theory:An Analy-sis of Decision under Risk[J].Econometrica,1979,47(2):263-291 [13] FAN Z P,ZHANG X,CHEN F D,et al.Multiple Attribute Decision Making Considering Aspiration-levels:a Method Based ON Prospect Theory[J].Computers & Industrial Engineering,2013,65(2):341-350 [14] 张晓,樊治平.基于前景理论的风险型混合多属性决策方法[J].系统工程学报,2012,27(6):772-781 ZHANG X,FAN Z P.Risk Hybrid Multi-attribute Decision Making Method Based on Prospect Theory[J].Journal of Systems Engineering,2012,27(6):772-781 [15] GOMES LFAM,LIMA MMPP.TODIM:Basic and Applica-tion to Multicriteria Ranking of Projects with Environmen-tal Impacts[J].Foundations of Computing and Decision Sciences,1992,16(4):113-127 [16] 樊治平,陈发动,张晓.考虑决策者心理行为的区间数多属性决策方法[J].东北大学学报(自然科学版),2011,32(1):136-139 FAN Z P,CHEN F D,ZHANG X.Interval Multiple Attribute Decision Making Method Considering the Mental Behavior of Decision Maker [J].Journal of Northeastern University (Natural Science Edition),2011,32(1):136-139 [17] KROHLING R A,DE SOUZA T.Combining Prospect Theory and Fuzzy Numbers to Multicriteria Decision Making[J].Expert Systems with Applications,2012,39(13):11487-11493 [18] FAN Z P,ZHANG X,CHEN F D.Extended TODIM Method for Hybrid Multiple Attribute Decision Making Problems[J].Knowledge-based Systems,2013,42(1):40-48 [19] 梁霞,姜艳萍,梁海明.考虑属性关联的C-TODIM决策方法[J].运筹与管理.2015,24(2):101-107 LIANG X,JIANG Y P,LIANG H M.C-TODIM Decision Method Considering Attribute Association [J].Operations Research and Management Science,2015,24(2):101-107 [20] SUGENO M.Theory of Fuzzy Integrals and Its App lications[D].Ph D Dissertation,Tokyo Institute of Technology,1974 [21] KUO M S,LIANG G S.A Novel Hybrid Decision-making Model for Selecting Locations in a Fuzzy Environment[J].Mathematicaland Computer Modelling,2011,54(1):88-104 [22] GRABISCH M,MUROFUSHI T,SUGENO M.Fuzzy Measure and Integrals[M].New York: Physica Verlag,2000 [23] GOMES L F,RANGEL L A.An Application of the TODIM Method to the Multicriteria Rental Evaluation of Residential Properties[J].European Journal of Opera-tional Research,2009,193(1):204-211 [24] 穆志民,曾守祯,张振荣.一种基于犹豫模糊集的多属性关联决策方法[J].数学的实践与认识.2014,44(20):228-234 MU Z M,ZENG S Z,ZHANG Z R.A Method of Multiple Attribute Association Decision Making Based on Hesitant Fuzzy Sets [J].Journal of Mathematics in Practice and Theory,2014,44(20):228-234 [25] KAPLAN R S,NORTON D.The Balanced Scorecard:Translating Strategy into Action[M].Boston:Harvard Business School Press,1996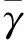
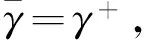
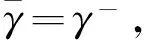
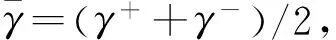
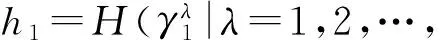
1.2 模糊测度
2 属性关联TODIM方法
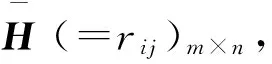
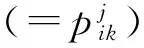
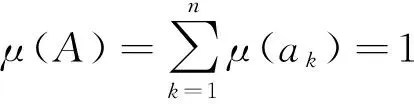
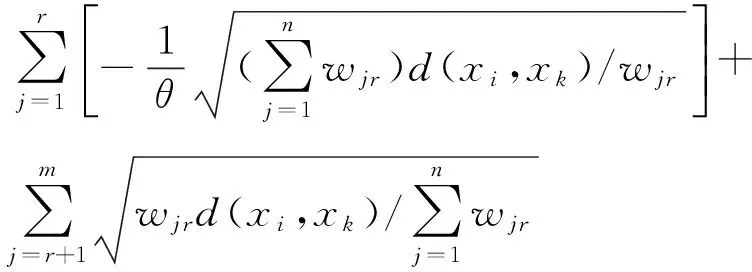
3 算例分析
3.1 算 例

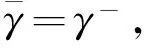


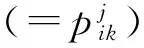
3.2 参数的敏感性分析
4 结 论

