基于力磁耦合效应的金属磁记忆仿真研究*

钱 康， 尹爱军，2

(1.重庆大学 机械工程学院，重庆 400044；2.重庆大学 机械传动国家重点实验室，重庆 400044)

0 引 言

钢铁等铁磁性金属材料在现代化工业中占有重要地位，被广泛地应用于各行各业。但是铁磁构件在制造加工阶段以及使用服役过程中通常承受着各种动载荷或者交变载荷的作用[1]，这使得铁磁构件形成局部的应力集中，应力集中区域的存在很容易造成设备、零部件失效，爆炸等事故的发生，因此对铁磁材料进行无损检测是生产安全的重要过程。但是常规无损检测技术对于构件的早期缺陷，检测成功率较低，常会因为未能及早发现机器装备中的损伤而造成不可估量的经济损失甚至安全事故。

金属磁记忆检测方法是一种近年来被发现并运用的无损检测方法[1]，它无需外界磁场的激励作用，可直接以地磁场为激励源，通过检测拉伸应力引起的残余漏磁场，即可对铁磁材料的应力集中程度和损伤等实现早期检测诊断，为金属疲劳分析、计算剩余寿命以及工艺结构设计提供良好的参照条件。因此，研究基于金属磁记忆的力磁耦合现象可以对铁磁性材料构件的安全使用有着指导作用，有效地防止因构件缺陷损伤造成的经济损失和安全事故[2-3]。

本文主要在理论计算分析的基础上，通过有限元仿真进行对比验证拉伸应力变化对磁记忆信号的影响。

1 基本理论

1.1 力磁效应耦合模型

金属磁记忆是在地球磁场的磁化作用下，铁磁材料因非线性周期性载荷作用，内部的磁畴组织发生不可逆的重新排列，从而使得应力集中区域发生磁场突变，并通过漏磁场显现在试件表面的“自磁化”现象，因此其本质是一种力磁耦合现象[4-5]。

铁磁材料的磁导率与外加磁场、载荷的关系可由力磁耦合关系式表示：

μ=μ1(1+bH/μ1)(a0+a1|σ|men|σ|)(1)

其中，μ是受载荷作用后的铁磁材料磁导率；μ1是铁磁材料的初始磁导率；H是外部施加作用于铁磁材料的磁场大小；a0，a1，m，n是常数，由应力以及载荷作用方向决定；b是常数，由铁磁材料性质决定；σ是外部施加作用于铁磁材料的应力大小。

由式(1)可以看出，外加磁场、载荷共同决定了受载荷作用后的铁磁材料磁导率。

根据45号钢的材料相关参数可知，b=2.5；μT=285；地磁场H=39.8 A/m。与载荷相关参数则依据载荷大小进行确定，其值如下[6]：

当σ<50 MPa 时，a0=0.768 04，a1=0.009 16，m=1.904 12，n=-0.033 53；

当 σ≥50 MPa 时，a0=-0.004 47，a1=0.041 08，m=1.554 99，n=-0.031 48。

利用式(1)，可得出 45号钢在拉伸载荷下，磁导率与应力的变化关系，如图1所示。

σ/MPa图1 45号钢磁导率与应力的变化关系Fig.1 The relation between permeability andstress of No.45 steel

1.2 磁偶极子模型

磁偶极子理论认为：应力集中部位的磁记忆信号由正负的磁偶极子产生。受应力作用的铁磁构件，其应力集中区域的磁记忆信号分布情况根据磁偶极子模型推导出其函数关系式[6-8]。

如图2所示，假定铁磁构件应力集中部位为一矩形槽，矩形缺陷长度为2l、宽度为2w、深度为d。用有限长度的磁偶极带模拟矩形缺陷，矩形缺陷两侧磁偶极带是极性相反、面磁荷密度ρs相等、距离为2w、深度为d的两个磁荷面。在假设缺陷口以及其他部位没有磁荷分布的情况下，矩形缺陷空间任一点P(x0，y0，z0)产生的漏磁场为

其中，μ0为真空中的磁导率。

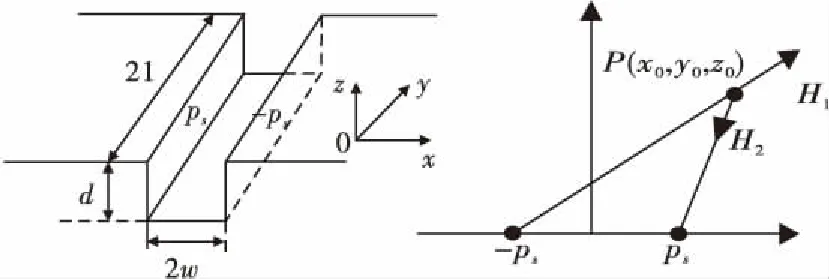
(a) 磁偶极子三维模型 (b) 极性相反的磁荷产生的场强图2 矩形缺陷模型的磁偶极子三维模型Fig.2 Three-dimensional model of magnetic dipolefor rectangular defect model

1.3 漏磁场计算

将缺陷模型简化为图3，缺陷宽度为2w，深度为d，h为应力集中区上端与试件表面的距离，z为提离值。

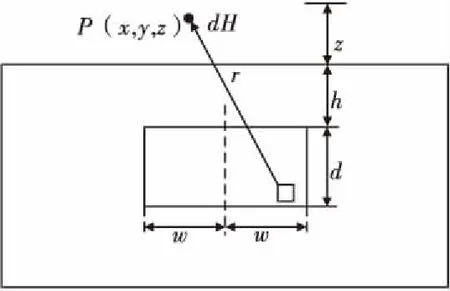
图3 矩形状缺陷简化模型Fig.3 The simplified model of moment shape defects

利用磁偶极子模型得到漏磁场X分量和Y分量的磁感应强度分量表达式：

(3)

(4)

2 力磁效应的理论计算

由金属磁记忆检测法的原理[7-10]可知，在轴向拉伸应力作用下铁磁体内部的磁畴组织发生了定向和不可逆的重新取向，从而使得应力集中区域周围的磁记忆信号发生变化。当拉应力增加时，铁磁性材料中磁畴的磁矩方向趋向一致，最终在应力或应变集中处积聚大量磁化能形成较强的漏磁场，表现为切向分量(X分量)存在峰值，法向分量(Y分量)存在过零点，梯度值K出现极值。图4表示45号钢分别在50 MPa、100 MPa、150 MPa、200 MPa、250 MPa的拉应力作用下的磁记忆信号分布及垂直分量的梯度值。

从图4可以看出：试件表面的磁记忆信号在宏观上曲线走势大致相同，其大小分布与载荷强度存在正相关关系；在试件中部即x=60 mm处，磁信号法向分量始终过零点，不受载荷大小的变化而发生位置改变；梯度值左右两侧的分布关于x轴的中线

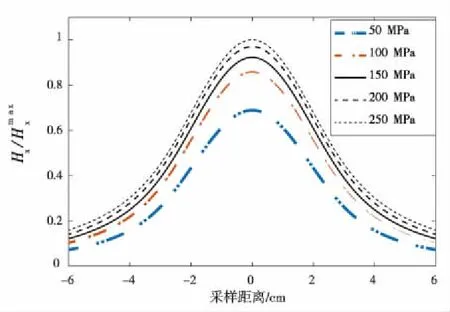
(a)X分量

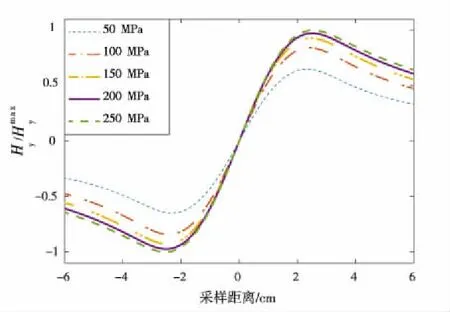
(b)Y分量

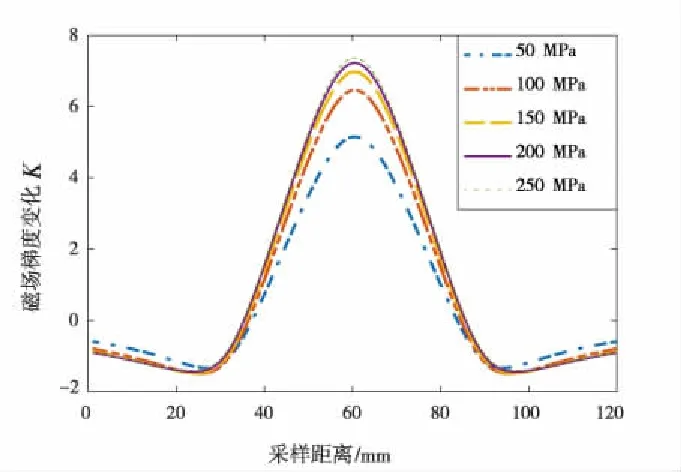
(c)磁记忆信号Y分量的梯度值图4 磁记忆信号分布及其Y分量梯度Fig.4 Distribution of magnetic memory signaland its Y component gradient

呈轴对称，且梯度的幅值随载荷增加而增大，在缺陷处梯度值的变化幅度明显，在x轴中点处出现极值。

3 有限元仿真

3.1 力磁耦合仿真

本文的力磁耦合仿真分析[11-12]是利用ANSYS中的Static Structural和Maxwell两个模块进行静力学和电磁学的力磁耦合仿真分析，流程如图5所示。

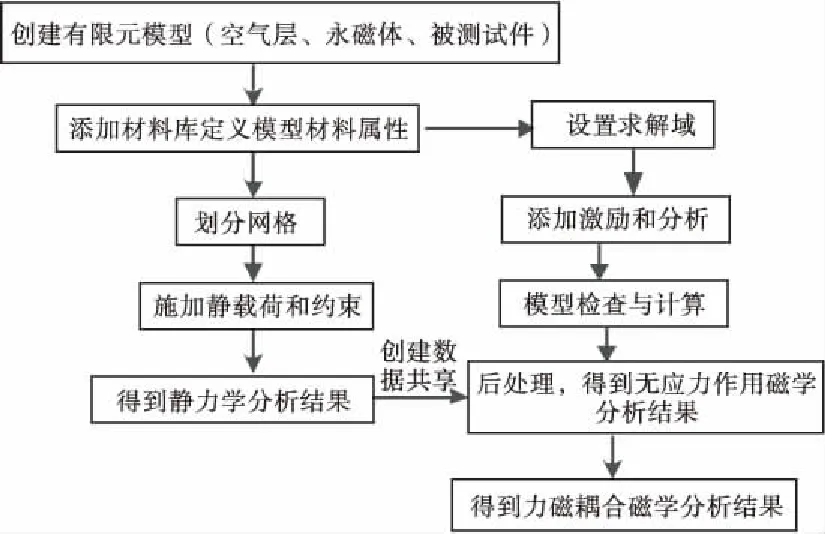
图5 力磁耦合仿真流程图Fig.5 Flow chart of force magnetic coupling simulation

3.2 仿真模型建立及参数设置

有限元仿真模型由求解域(空气层)、两块永磁铁、衔铁以及被测试件组成。通过对两块永磁铁进行参数设置，利用永磁体产生的磁场来模拟地磁场，磁力线分布如图6所示。为得到较好的仿真效果，仿真模型在尺寸设置上要求永磁体尺寸远大于被测试件。

图6 仿真模型的磁力线分布Fig.6 Distribution of magnetic lines in simulation model

地球磁场强度为30～60 A/m，由图7所示可知，两个永磁铁之间的磁场强度为52.451～55.999 A/m，符合实际情况，所以该模型参数设置正确。

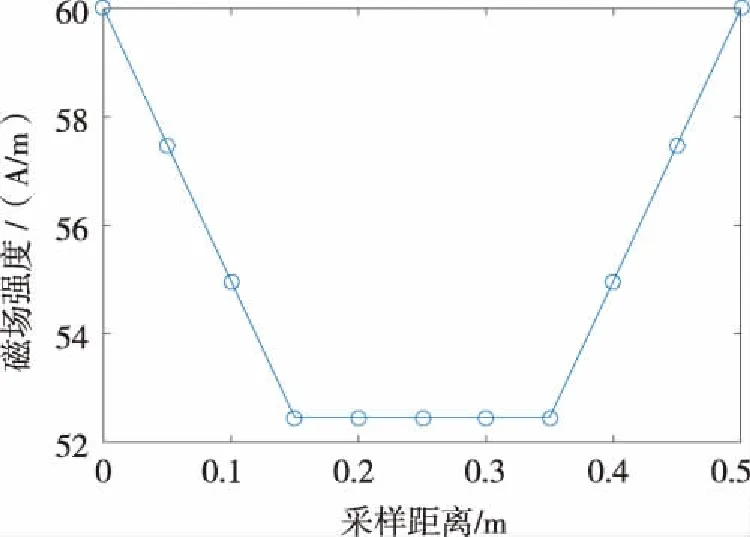
图7 永磁铁间隙磁场强度Fig.7 The magnetic field intensity of permanent magnet

研究试样为中心含有小孔的45号钢平板，其尺寸大小如图8所示，其参数设置如表1所示。

图8 试件尺寸大小Fig.8 The size of specimen表1 试件有限元模型参数设置Table 1 The finite element model parameter settingof test specimen

单位E/GPavσs/MPaμT数值2090.269355285

如图9所示，对被测试件进行网格划分得到试件的有限元模型。

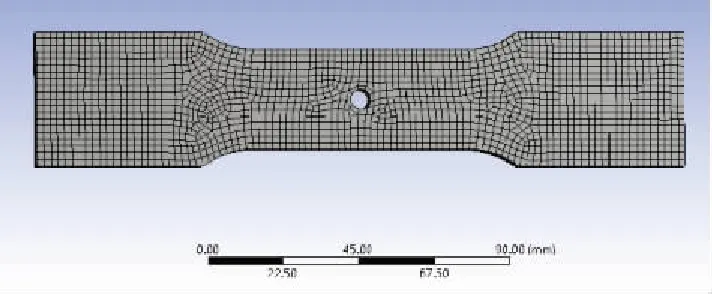
图9 试件的有限元模型Fig.9 Finite element model of specimen

3.3 力磁耦合仿真结果分析

将图8所示的被测试件一端固定，另一端分别施加50 MPa、100 MPa、150 MPa、200 MPa、250 MPa的拉应力。

根据ANSYS Workbench仿真结果可知，应力集中均发生在中心孔两侧，提取不同应力作用下，应力集中处的最大应力值，绘制出图10。从图10可以看出，随着外加应力的增大，中心孔处存在的最大应力随之增大，且呈线性增长趋势。

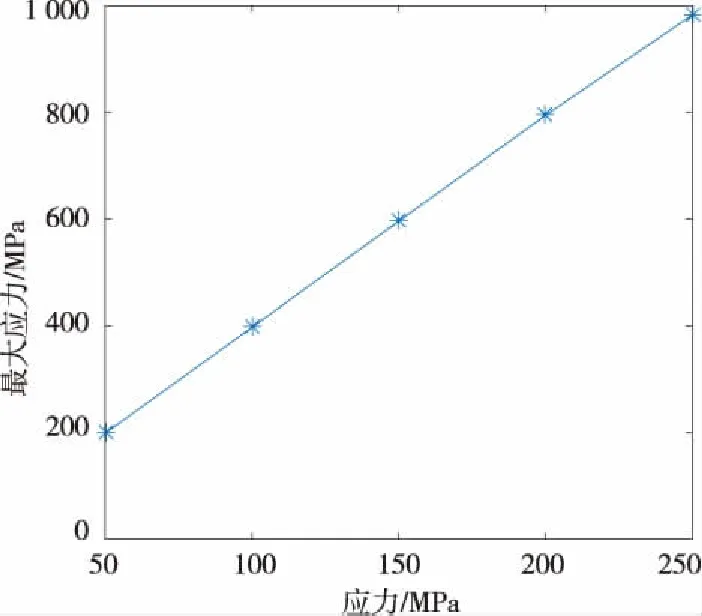
图10 中心孔处最大应力变化趋势Fig.10 Variation trend of maximum stress at center hole

创建数据共享，将静力学分析的结果作为外载荷传递到Maxwell模块进行磁学分析，按照扫描路径，在提离值0.5 mm时，得到中心孔周围磁记忆漏磁场X分量和Y分量的分布情况如图11所示。

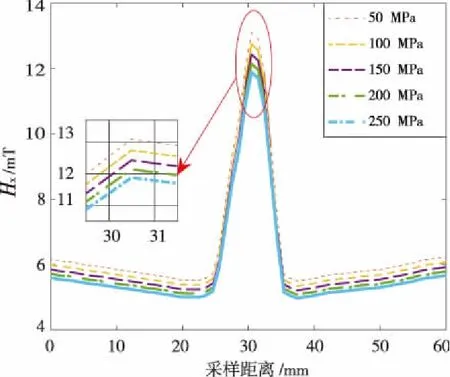
(a)X分量

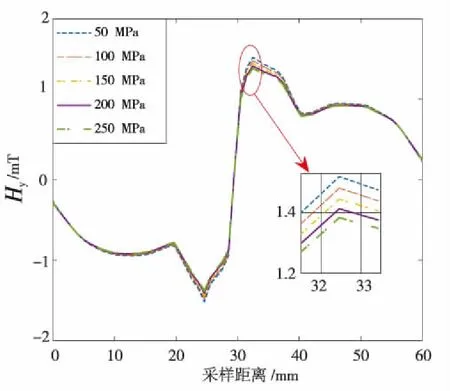
(b)Y分量

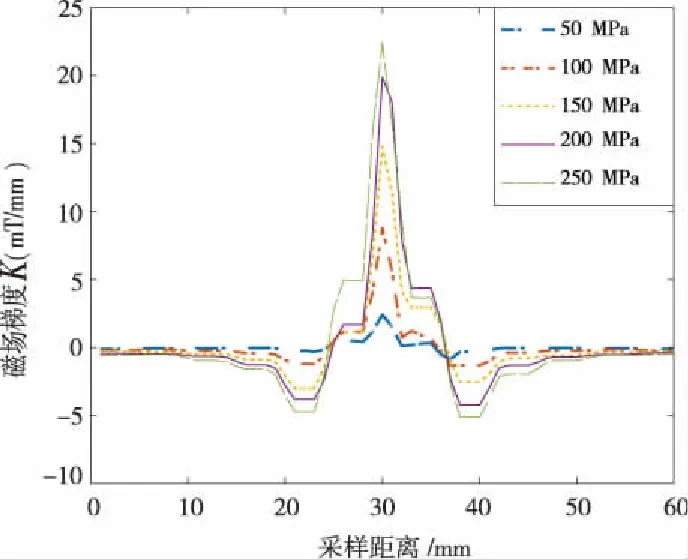
(c)Y分量梯度值图11 磁记忆信号分布及其Y分量梯度Fig.11 Distribution of magnetic memory signal and its Ycomponent gradient

从图11可以看出：

磁记忆漏磁场X分量和Y分量均随着外加应力的增大而增大；

随着外加应力的增大，后阶段相比于初始阶段漏磁场X分量和Y分量的峰值变化更加剧烈，峰值增幅增加，这是由于当试件所受应力达到一定范围时，试件磁导率减小，磁阻增大。

在试件中心位置，磁场梯度出现最大值，对应磁记忆信号垂直分量过零点位置。 仿真结果与理论计算一致，体现出应力集中导致的金属磁记忆现象的典型特征：漏磁场水平分量出现最大值而垂直分量出现过零点，同时在过零点位置磁场梯度变化最大，存在峰值。这证实了有限元仿真的可靠性，本文的有限元模型可用于铁磁材料的拉伸磁记忆有限元分析。

4 结 论

根据已知的力磁效应关系表达式和磁偶极子模型推导出磁记忆信号的表达式，并通过理论分析不同拉伸应力下磁记忆信号分布及其垂直分量梯度的变化规律。对45号钢构件进行了有限元建模分析，得出不同载荷下应力集中对铁磁构件磁记忆信号的变化规律，可为工程早期损伤的识别提供参考。后续将会进行金属拉伸变形检测试验进而验证理论计算与有限元仿真所得出的结论。

[1] DUBOV A A.Development of a Metal Magnetic Memory Method[J].Chemical & Petroleum Engineering，2012，47： 837-839

[2] 王威，曾发荣，苏三庆，等.基于磁记忆的受弯钢梁力-磁效应试验[J].材料科学与工程学报，2016(1)：109-114

WANG W，ZENG F R，SU S Q，et al.Experimental Research on Magnetic Mechanical Effectiveness of Bending Steel Beam Based on Metal Magnetic Memory [J].Journal of Materials Science and Engineering，2016(1)： 109-114

[4] 赵珍燕，任尚坤，杨梅芳，等.不同材料在不同应力状态下的磁记忆信号特征[J].钢铁研究学报，2017(2)：123-127

ZHAO Z Y，REN S K，YANG M F ，et al.Magnetic Memory Signal Characteristics of Different Materials under Different Stress States [J].Journal of Iron and Steel Research，2017(2)： 123-127

[5] 刘斌，张威，杨茗涵，等.基于第一性原理的力磁耦合模型研究[J].仪表技术与传感器，2014(3)：76-78

LIU B，ZHANG W，YANG M H，et al.Study on the Force-Magnetic Coupling Model Based on First-Principle [J].Instrumentation Technology and Sensors，2014(3)： 76-78

[6] 习小文.铁磁构件应力磁化及反转效应的数值模拟与试验研究[D].南昌：南昌航空大学，2015

XI X W.Numerical Simulation and Experimental Research of Stress Magnetism and Magnetization Reversal Effect on Ferromagnetic[D].Nanchang:Nanchang University of Aeronautics，2015

[7] 代汝林，李忠芳，王姣.基于ABAQUS的初始地应力平衡方法研究[J].重庆工商大学学报(自然科学版)，2012(9)：76-81

DAI R L，LI Z F，WANG J.Research on Initial Geo-Stress Balance Method Based on ABAQUS[J].Journal of Chongqing Technology and Business University (Natural Science Edition)，2012(9)： 76-81

[8] 权大赫，丁红胜，金光秀.弹塑性变形阶段力磁效应的有限元模拟[J].测试技术学报，2015(3)：200-207

QUAN D H，DING H S，JIN G X.Finite Element Simulation of Magneto-Mechanical Effect in Elastic-Plastic Deformation Phases [J].Journal of Test and Technology，2015(3)： 200-207

[9] 姚结艳.基于力/磁耦合作用的再制造构件磁记忆检测研究[D].合肥：合肥工业大学，2014

YAO J Y.Research on Metal Magnetic Memory Testing for Remanufacturing Components Based on Stress-magnetic Coupling Mechanism[D].HeFei：HeFei University of Technology，2014

[10] 陈健飞，张茜云，刘海波，等.基于有限元分析的磁记忆关联模型试验[J].无损检测，2016(11)：37-40

CHEN J F，ZHANG Q Y，LIU H B，et al.Experiment of Magnetic Memory Association Model Based on Finite Element Analysis [J].Nondestructive Testing，2016，(11)： 37-40

[11] 刘国奇，付任珍，李新蕾，等.紧凑拉伸试样应力场仿真与磁记忆效应分析[J].无损探伤，2014(6)：17-20

LIU G Q，FU R Z，LI X L，et al.Compact Tension Specimen Stress Memory Field Simulation with F and Magnetic Effect Analysis [J].Nondestructive Testing，2014(6)： 17-20