一种基于加权马氏距离的TOPSIS改进评价法及其应用*
王 韦 霞
(安徽机电职业技术学院 基础教学部,安徽 芜湖 241003)
TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)评价法属多指标、多方案的排序法,它的中心思想是:通过构造评价体系的正、负理想解向量,计算每个评价方案到正、负理想解向量的距离,再求出每个评价方案和最优方案的相对贴近度来对方案进行排序,从而选出最优方案。
1 传统TOPSIS法及其局限性
设有n个评价方案Ai(i=1,2,…,n)及m个指标Cj(j=1,2,…,m),xij为评价方案Ai在指标Cj下的指标数据。传统的TOPSIS方法采用如下操作步骤:
步骤1 用向量归一化法对评价指标进行预处理,即:
步骤2 构造加权规范评价矩阵Z=(zij)n×m,其中:
zij=wjyij(i=1,2,…n;j=1,2,3,…,m)
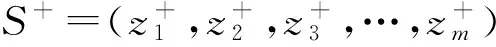
步骤4 计算各评价方案到正、负理想解的欧氏距离。
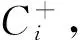
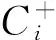
2 传统TOPSIS法及其局限性
传统的TOPSIS法存在如下局限性[1-2]:
(1) 由步骤2发现,权重采用主观判断且事先作用于标准数据中,不仅缺乏客观合理性,而且容易导致TOPSIS现逆序现象。
(2) 由步骤3发现,增加或减少新方案可能导致正、负理想解改变,也容易出现逆序现象。
(3) 由步骤4、步骤5发现,欧式距离测量存在问题:当两不同评价方案到最优、最劣方案的欧式距离相等时,此时无法根据贴近度比较优劣。同时,当评价指标数据相关性显著时,使用欧式距离容易出现误判。
3 改进的TOPSIS法原理及步骤
为了解决上述局限性,提出一种基于加权马氏距离的TOPSIS法,改进如下:
(1) 正、负理想点选择的改进方法:将评价指标转化为效益型指标,借助极差变换法转化为标准化矩阵,即:
对效益型指标:
对成本型指标:
显然,正、负理想解为:S+=(1,1,1,…,1),S-=(0,0,0,…,0),不会随着新方案的增加或减少而改变。
(2) 将评价方案到正、负理想解的欧式距离改用加权的马氏距离定义。
假设各方案Ai标准化后的数据指标值Si(si1,si2,…,sim)及正、负理想解均来自于均值为μ,协方差阵为∑的总本样本空间G,则方案Ai到正、负理想解的加权马氏距离d+(Si,S+)、d-(Si,S-)定义为
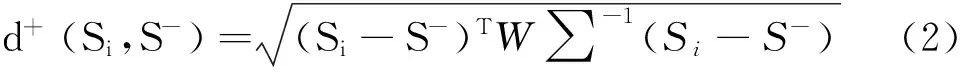
其中W=diag(w1,w2,…,wm)为指标Cj(j=1,2,…,m)的权重。由矩阵的知识可知,要使d+(Si,S+),d-(Si,S-)存在,要求协方差阵非奇异,且W∑-1正定,则W∑-1首先必须为对称矩阵,即要求w1=w2=…=wm,但实际问题中指标间往往存在差异性,各指标权重取值一样显然不合理[5]。为使加权合理以及计算的d+(Si,S+),d-(Si,S-)有意义,采取如下做法[3-7]:
令Λ=diag(λ1,λ2,…,λm),其中λ1,λ2,…,λm为∑的特征值,U=(e1,e2,…em)为特征值对应的特征向量组成的正交基,做变换fi=UTSi(i=1,2,…,m),则fi=(fi1,fi2,…,fim)的协方差阵Λ满足UT∑U=Λ,利用上述定义的评价方案到正、负理想解的距离(式(1)、式(2)) ,fi到正理想解的加权马氏距离为
同理可得:
由tr(Λ)=tr(∑),可知变换后的fi=(fi1,fi2,…,fim)(i=1,2,…,n)没有改变原先Si(si1,si2,…,sim)(i=1,2,…,n)之间的差异程度,故可用变换后的d+(fi,S+)、d-(fi,S+)代替方案Ai到正、负理想解的加权马氏距离,此时WΛ-1必是正定的。
4 案例分析
评价企业综合实力问题:为系统地分析某IT类企业的经济效益,选择8个不同的利润指标,对15家企业进行了调研,得到如表1所示的数据。
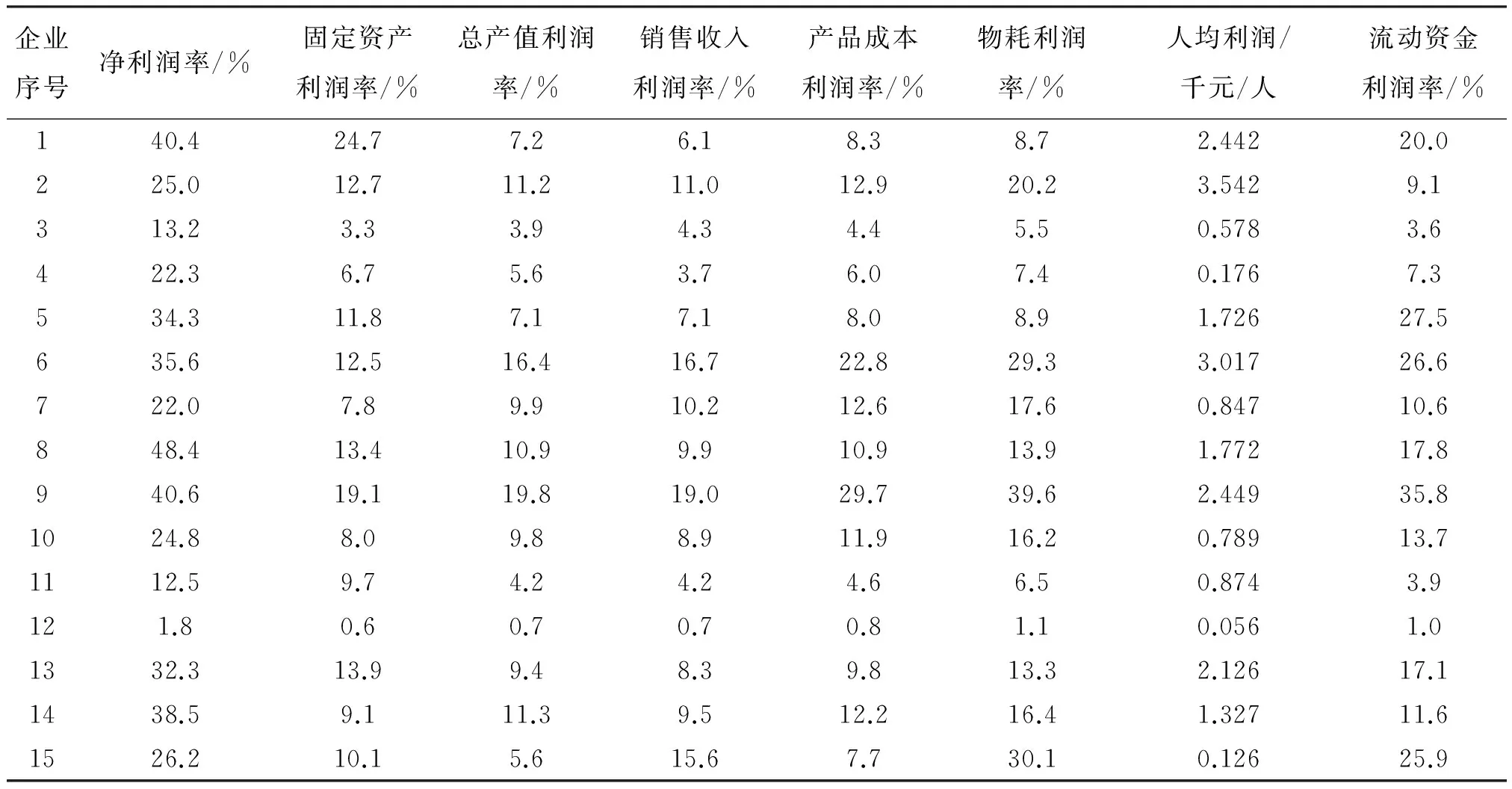
表1 企业综合实力评价Table 1 Evaluation of enterprise comprehensive strength
根据式(3)改进的TOPSIS法计算得出方案Ai标准化后的数据指标矩阵S如下:
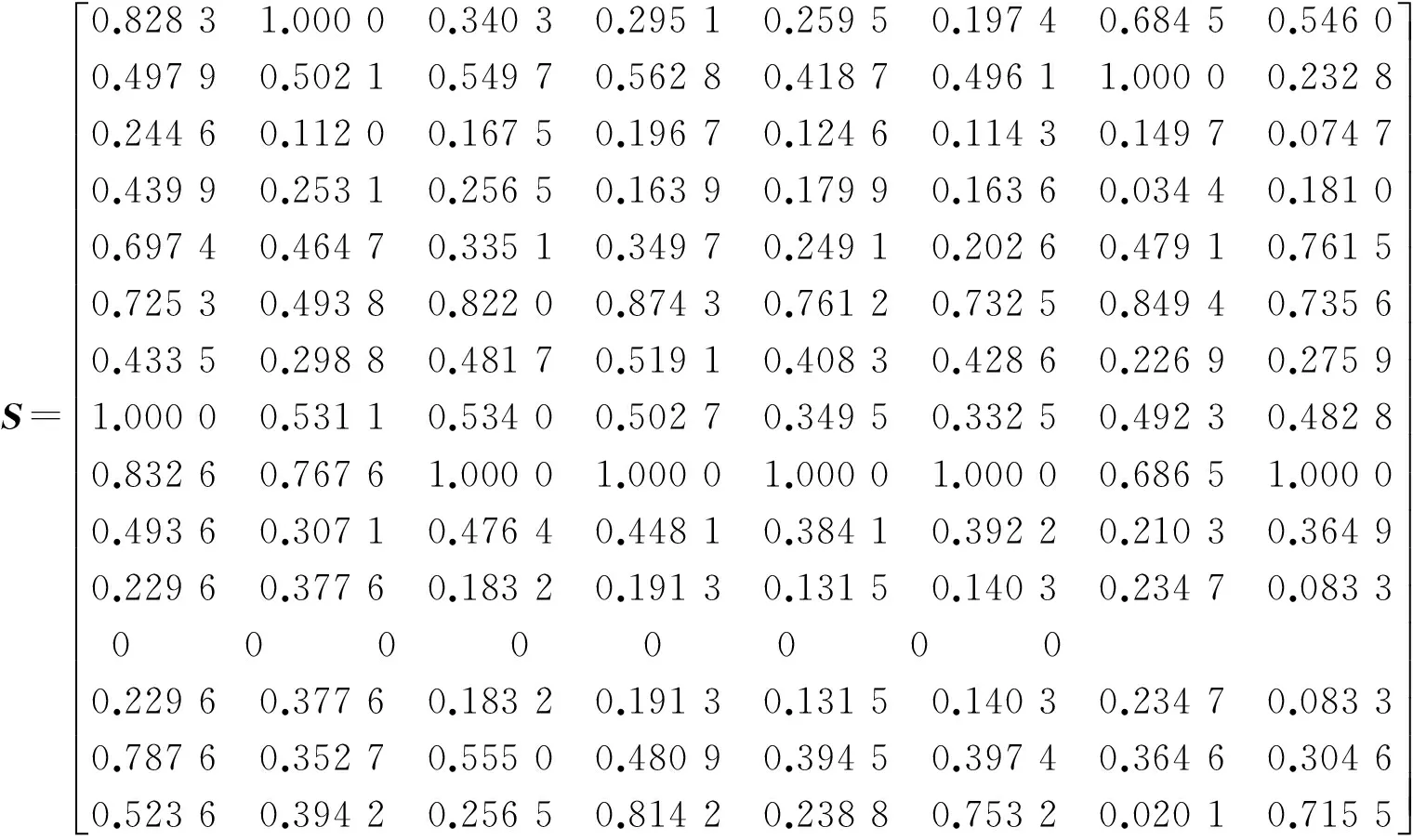
显然此时的正、负理想解为:S+=(1,1,1,…,1),S-=(0,0,0,…,0)。计算S的协方差阵Σ及其特征向量组成的正交基U分别为
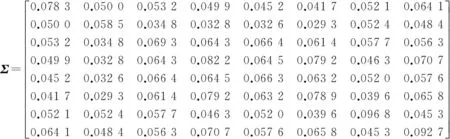
U=

-0.1946-0.14360.35770.02560.64410.43850.30280.33770.06580.1159-0.1169-0.6860-0.39320.26910.45190.25840.71030.0946-0.2839-0.11880.4221-0.2768-0.05830.3657-0.07140.68400.4730-0.0037-0.1349-0.0464-0.36130.3905-0.65600.0367-0.5371-0.14670.1862-0.2724-0.15410.35440.0442-0.69160.2970-0.2221-0.2211-0.0930-0.43600.3668-0.0412-0.09360.17860.3948-0.2412-0.53150.58730.34090.1193-0.0266-0.38140.5366-0.30400.5397-0.10680.3957
设各指标的权重矩阵为W=diag(w1,w2,…,w8),采用专家评判法求得各指标的权重向量W=diag(0.25,0.2,0.15,0.1,0.1,0.1,0.05,0.05),利用改进后的TOPSIS评价法求得方案Ai到正、负的加权马氏距离及到正理想解的相对贴近度如表2所示,改进后的TOPSIS法与改进前的TOPSIS法对各评价方案按由优到劣的排序如表3所示。从改进前、后的TOPSIS法的结果可见,第一名、第二名以及最后一名结果一样,反映了两种方法在评判方案优劣性方面,某种程度上是一致的,而中间排名顺序发生变化,主要原因是评价指标数据重复信息较多。
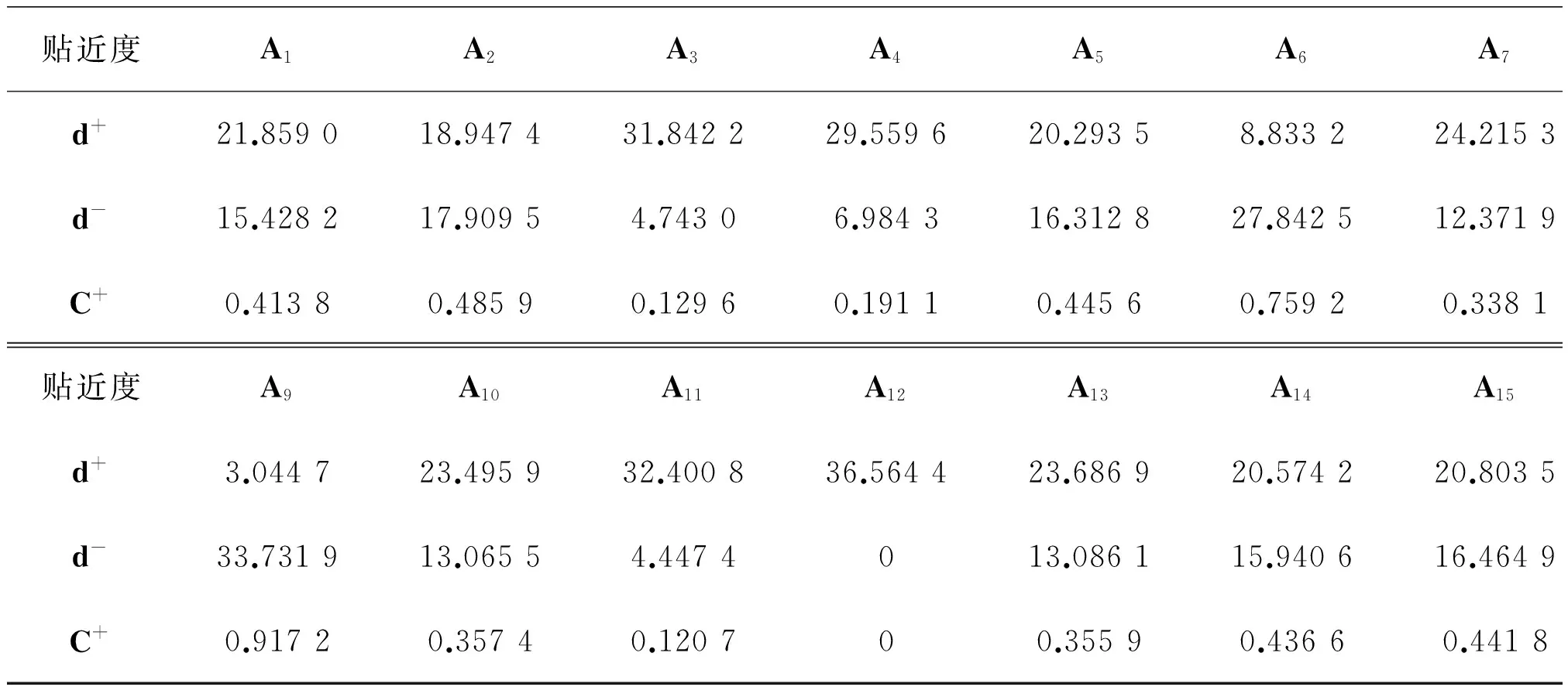
表2 各评价方案相对贴近度Table 2 Relative closeness of evaluation scheme

表3 改进前、后TOPSIS法结果对比Table 3 The TOPSIS method results before and after improvement
5 结 语
与传统的TOPSIS方法相比,改进后的TOPSIS方法有如下优点:
(1) 将评价指标转化为效益型指标,将相对正、负理想解转化为绝对正、负理想解,消除传统TOPSIS方法容易产生的逆序现象。
(2) 同时,将评价方案做正交变换,利用变换后的评价方案到正、负理想解的马氏距离代替传统欧式距离,不仅解决了评价指标信息相关性影响评价结果问题,而且也解决了协方差矩阵奇异时马氏距离不存在问题。
(3) 采用主观方法对各指标赋权与利用各评价指标对评价方案的方差贡献率赋权相结合的方法,充分利用了评价对象信息的客观性及专家经验知识的主观性,通过宏观及客观调控,进一步提高了评价结果的可靠性。
[1] 黄永生.基于熵值与TOPSIS在战略供应商选择的应用[J].物流科技,2016(3):121-123
HANG Y S.Application of TOPSIS Method in Strategic Supplier Selection Based on Entropy Weight [J].Logistics Sci-Tech,2016(3)121-123
[2] 陈伟.关于TOPSIS法应用中的逆序问题及消除的方法[J].运筹与管理,2005(3):39-43
CHEN W.On the Problem and Elimination of Rank Reversal in the Application of TOPSIS Method [J].Operation Research and Mana-gement Science,2005(3):39-43
[3] 文望,陆新.马氏综合权重距离判别法在中小型滑坡灾害评估中的应用[J].后勤工程学院学报,2013(6):11-17
WEN W.LU X.Application of Mahalanobis Comprehensive Weighting Distance Discriminant Method in Stability Assessment of Small and Medium Landslide [J].Journal of Logistical Engineering University,2013(6):11-17
[4] 赵琳,罗汉,刘京.加权马氏距离判别分析方法及其权值确定—旅游信息服务系统的智能推荐[J].经济数学,2007(2):185-188
ZHAO L,LUO H,LIU J.Weighted Mahalanobis Distance and the Weight-Determining Method[J].Mathematics in Economics,2007(2) :185-188
[5] 何桢,吕海利.用加权马氏距离法进行多响应产品设计的一种改进[J].组合机床与自动化加工技术,2007(2):88-91
HE Z,LU H L.An Improvement to the Method of Multires-ponse Product Design Using Weighted Mahalanohis Dis-tance[J].Modular Machine Tool &Automatic Manufac-turind Techn-ique,2007(2): 88-91
[6] 王正新.基于马氏距离的TOPSIS决策方法及其应用[J].经济数学,2012(2):17-20
WANG Z X.Mahalanobis Distancd-based TOPSIS Decision Making Method and Its Application[J].Jouranl of Quantitative Economics,2012(2):17-20
[7] 张峰,谢振华,程江涛,等.基于主成分的改进马氏距离TOPSIS方法[J].火力与指挥控制,2015(3):92-95
ZHANG F,XIE Z H,CHENG J T,et al.Method to Improved Mahalanohis Distance of TOPSIS Based on Principal Component[J].Fire Control & Command Control,2015(3):92-95

