中考数学文化题的赏析与探讨
顾为云

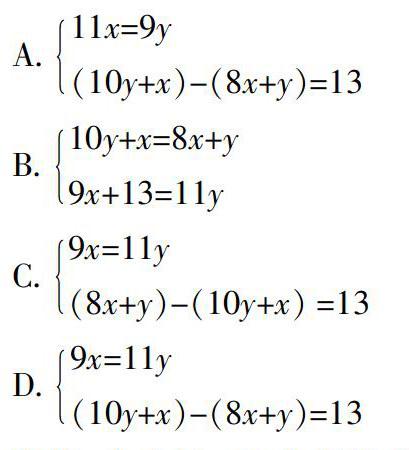
[摘 要] 数学文化题是中考的新题型,问题以古典著作为背景,融合了数学知识内容和思想方法. 本文以近几年的中考题为例,分析问题形式,探讨解题策略,与读者交流学习.
[关键词] 数学文化;中考数学;定理;证明;拓展;应用
近几年的中考中,出现了众多以数学文化内容为背景的考题,该类考题具有情感熏陶和知识考查的双重功能,理解和学习数学文化题有助于学生了解数学的发展历史,深刻理解数学的知识内容,下面将详细解读中考数学中的文化类考题.
对著作问题的解析
在古代数学著作中涉及众多的问题,以著作问题为背景,用现代数学语言求解是中考中数学文化的典型问题. 该类题一般给出古语问题以及译文,需要学生理解问题信息,探寻解题思路,主要考查学生相应的数学知识.
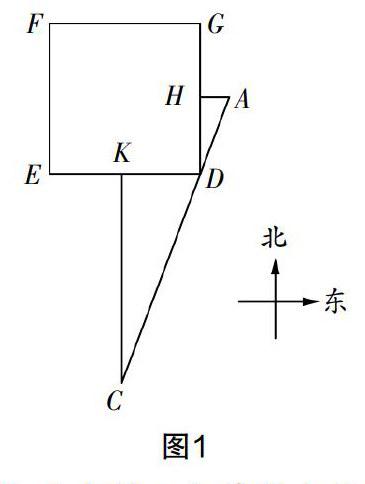
例1 (2018年泰安卷第17题)《九章算术》是中国传统数学最为重要的著作,在“勾股”章节有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话翻译,大意为:如图1所示,DEFG为一边长为200步(“步”为古代长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出去东门15步远的点A处有一树木,试求出去南门多少步可以恰好看到位于点A处的树木(即点D位于直线AC上)?请计算KC的长为_______步.
赏析 本题来源于古代数学著作《九章算术》,属于平面几何问题,解题的重点在于结合几何图形理解著作译文,从中提炼关键条件,然后构建解题思路. 本题目涉及三角形相似和相似性质等几何知识,由图形相似构建线段对应关系来完成求解.
对著作问题的模型构建
构建古代著作问题的研究模型是中考数学较为常见的考题,该类题一般给出著作问题的相关译文,要求利用现代数学思想建立研究模型,最为典型的问题是利用方程思想,建立解决问题的方程组.
例2 (2018年广州卷第8题)《九章算术》是我国古代数学的经典著作,书中有这样一个问题:“今有黄金九枚,白银一十一枚,称之重适等 ,交易其一,金轻十三两,问金、银各重几何?”大致意思是:甲袋子中装有黄金9枚(每枚黄金重量相等),乙袋中装有白银11枚(每枚白银重量相等),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?如设每枚黄金重x两,每枚白银重y两,根据题意可得()
分析 由选项可知本题目需要根据著作的信息条件列出求解方程,即建立问题研究的数学模型,属于二元一次方程实际应用题. 解题的具体思路是:依据方程思想,从题干信息中提炼等量关系,然后将其用数字符号表示.
解答 黄金9枚=白银11枚,即总质量相等,可得9x=11y.
赏析 本題目同样来源于数学著作《九章算术》,需要依据问题信息构建求解的二元一次方程组. 基本解题策略是理解问题信息,从中提炼等量关系,将其转化为对应的数学语言,并用数学符号表示,是方程思想的应用.
对著作定理的推导证明
著作定理的推导证明题一般以古代数学定理为背景,以完善定理证明过程为出题形式,主要考查学生解题的思维过程. 解题时首先需要理解定理证明的思维方法和构建思路,然后结合问题信息探求证明条件,几何定理的证明是其中最为常见的问题.
例3 (2017年北京卷第20题)数学家吴文俊院士非常重视我国古代数学家贾宪提出的“从长方形对角线上任意一点作它的两条分别平行于两邻边的直线,则所容两长方形的面积相等(如图2所示)”这一推论,他从这一推论出发,利用“出入相补”原理还原了《海岛算经》的九题古证. (上述材料来自于《古证复原的原理》《吴文俊与中国数学》和《古代数学泰斗刘徽》)
请根据图2完成该推论的证明过程.
分析 本题目要求证明古法定理,是关于四边形面积相等的问题,考查的是四边形面积的计算和图形分割知识. 由题可知,具体证明思路是:利用割补法,将其分割为几个小三角形的组合,然后分别证明对应小三角形面积相等. 因此证明过程的第一步是对矩形的面积割补,则矩形EBMF面积大小等于△ABC分别减去两个小的三角形△AEF、△FMC,第二步是分别证明分割所用三角形的面积相等,即△ANF与△AEF的面积相等,△FGC与△FMC的面积相等.
解答 由矩形的对角线将其分割为对应相等的两个小三角形,可知证明过程为:
赏析 上述问题来源于吴文俊院士对古定理的还原,是典型的几何证明题. 证明的总体思路是分割图形,构建图形的面积关系,因此在完善证明过程中依据该策略来建立问题的证明条件,该类问题对学生的证明思维要求较高.
以著作文化为背景的解题应用
古典著作的文化信息同样在数学解题中有着极为广泛的应用,涉及数学的定理和思想方法. 以其为背景命制的拓展应用题通常给出相关的定理公式,要求利用定理求解实际问题,解题关键是理解定理,把握定理的适用条件.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
分析 题目给出了勾股数通解公式,求解n=1时一边长为5的直角三角形的其他边长,可以用m,n构建边长的表达式,然后从中选取符合题意的情形.
赏析 以数学文化为背景的拓展应用题具有较强的实用性,是对数学“学以致用”理念的贯彻. 上述以勾股数为背景,给出了相应的勾股数通式,以问题解决的形式考查学生知识的理解与应用能力,由于定理的条件限制,使得问题呈现多解情形,因此对学生的严谨思维具有较高的要求.
综上可知,数学文化题结合了文化信息与数学知识,是对数学教材的一种补充与拓展,学习求解数学文化题需要借助考题的导向作用,关注数学的经典著作,了解与教材内容相关的文化题材,尤其是教材中的定义与概念,需要结合其文化背景来加以理解. 以强化阅读能力为基础,培养数学文化思维是提升该类问题求解能力的关键.

