数学问题解答

2017年11月号问题解答

(解答由问题提供人给出)

2391凸四边形A1A2A3A4在直线l同一侧，A1A3与A2A4是凸四边形的两条对角线，△A2A3A4,△A1A3A4,△A1A2A4及△A1A2A3的面积分别是S1,S2,S3,S4.Ai至直线l的距离为di(i=1,2,3,4),则d1S1+d3S3=d2S2+d4S4.

(江苏如皋市教师进修学校 徐道 226500)

证明设A1→A2→A3→A4→Ai逆时针排列，Ai(xi,yi),yi>0,i=1,2,3,4,直线l的方程为y=0.

考察行列式

由于D第一列与第三列对应元素相等，故D=0.

又由行列式的性质

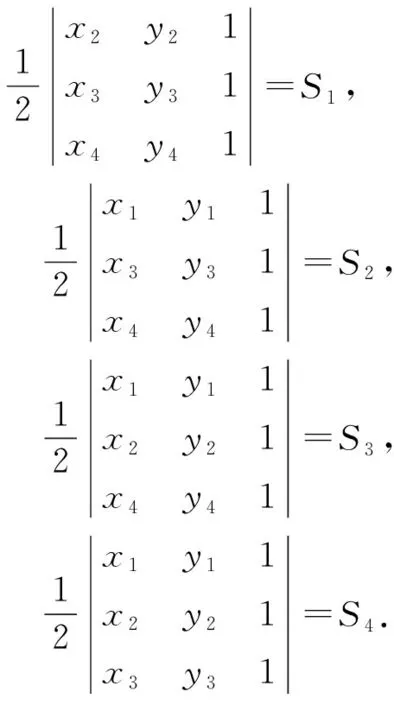
yl=di(i=1,2,3,4).

故d1S1-d2S2+d3S3-d4S4=0,结论获证.

2392如图，PAB、PCD分别是⊙O的两条割线，交⊙O于点A、B、C、D，AD与BC相交于点Q.若点M、N分别满足四边形MAQC，四边形NBQD都是平行四边形.证明:P、M、N三点共线.

(重庆市合川太和中学 袁安全 401555)

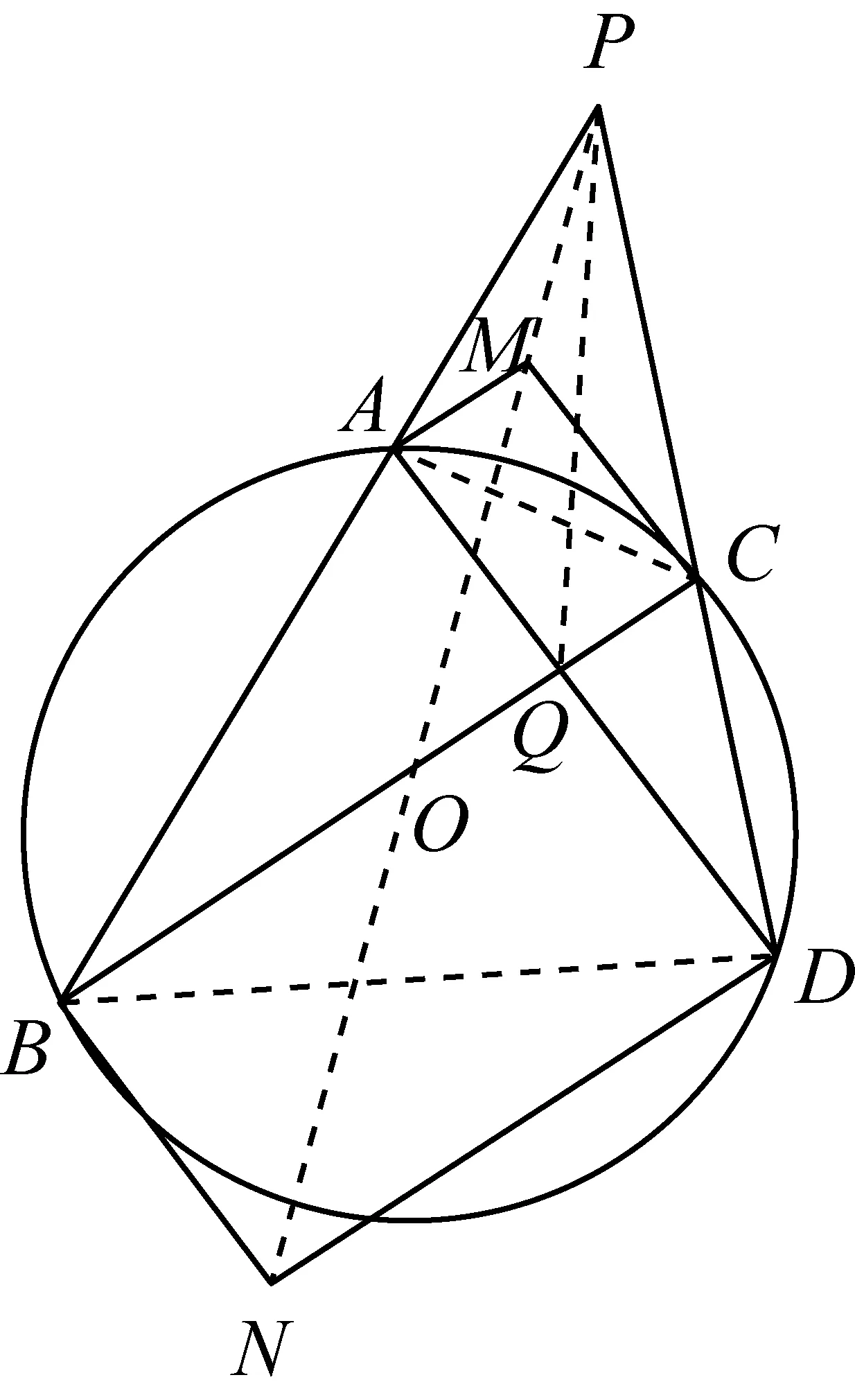
证明如图所示.

连接AC、BD、PQ、PM、PN.

则BN=QD,AM=QC.

易知△PAC∽△PDB，

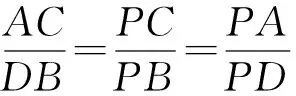
①

又易知△QAC∽△QBD，

②

由①,②得

又易得∠PBN=∠PBD+∠DBN

=∠PCA+∠ACB=∠PCQ.

于是△PBN∽△PCQ,

故∠BPN=∠CPQ.

又由①，②可得

而∠PAM=∠PBC=∠ADC=∠PDQ,

从而△PAM∽△PDQ,

进而∠APM=∠DPQ.

于是∠BPN=∠CPQ=∠DPQ=∠APM.

故P、M、N三点共线.

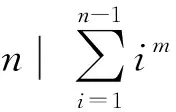
(浙江温州市区马鞍池东路1-408 陈克瀛 325000)

解n可唯一地表为n=3rb，其中r，b∈N+，(3 ,b)=1. 我们来证明以下两个结论：

证对r施行数学归纳法.

r=1时，由1k+2k≡2≢0 ( mod 3 )知结论成立；

假定r=d时结论成立；

今证r=d+1时结论也成立. 对此用反证法.

如果存在正偶数m，使得

(1)

变换(1)的左端和式得

(2)

用二项式定理展开(2)的右端并注意到：

“正整数u≥2⟹3d+1| 3du(特别地有

3d+1| 3dm)”之后，

对(2)取模3d+1得

由此和(1)并根据同余式的性质推出

而这与归纳法假定矛盾！这就证明了结论对于r=d+1也成立 . 命题A得证 .

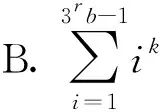
证b=1时，命题B即命题A.

以下设b>1. 用反证法. 如果存在正偶数m，使得

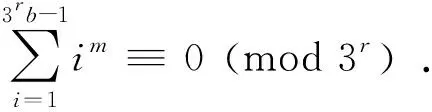
(3)

另一方面，对等式

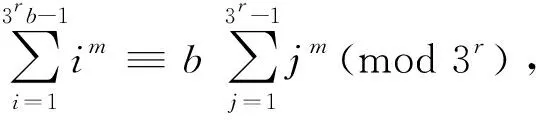
由此和(3)以及“( 3 ,b)=1⟹( 3r,b)=1”

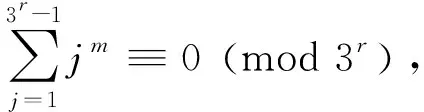
这与命题A矛盾！故命题B获证.

由B即知，不存在满足题述条件的正偶数.

注奇数n(n>1 )不是3的倍数，则

2394在等边三角形ABC中，D为边BC的中点，P为线段BD上异于端点的一点，延长线段AP交该三角形的外接圆于点Q，延长线段QD交AQ的垂直平分线MN于点M,证明：

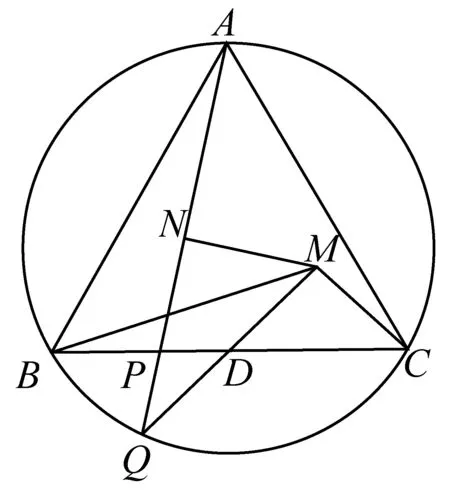
(河南省辉县市一中 贺基军 453600)

证明如图，连接AD,AM及QB,QC.

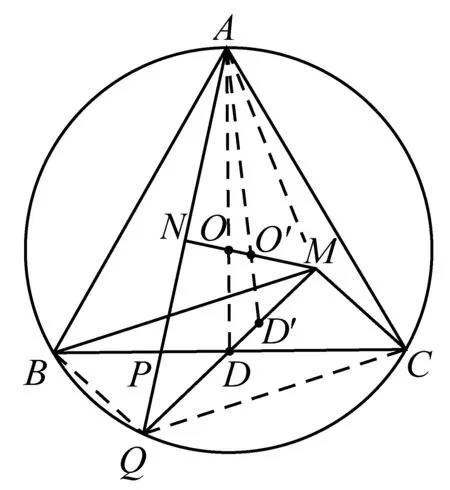
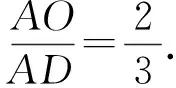
在△AQM中，QM的中点记为D′，

则AD′与MN的交点O′为该三角形的重心.

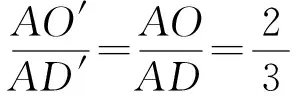
OO′∥DD′，即NM∥QM，这显然矛盾.

因此D,D′两点重合，D为QM的中点.

在四边形BQCM中，

因对角线BC与QM相互平分，

故该四边形为平行四边形，

从而有QB=MC，QC=MB.

在圆内接四边形ABQC中，由托勒密定理得

AB·QC+CA·QB=BC·AQ,

因AB=BC=CA, 故QC+QB=AQ.

在△BCQ中，易知

∠BQC=120°,∠BQP=∠CQP=60°,

又由三角形面积公式得

综上可得

2395已知△ABC三边长,面积,半周长,外接圆及内切圆半径分别为a,b,c,Δ,s,R,r.则

(1)

(黄兆麟 天津水运高级技工学校 300456)

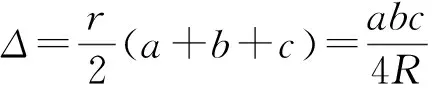
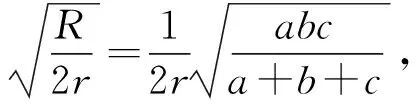
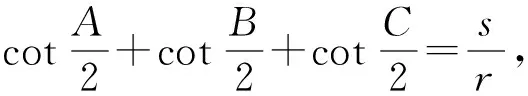
那么有

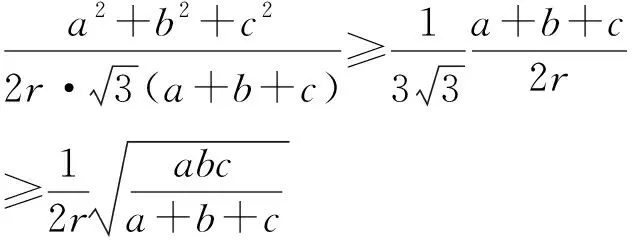
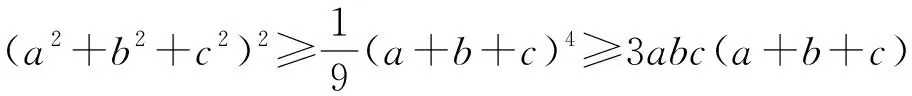
(2)

而显然有 3(a2+b2+c2)≥(a+b+c)2,

两边平方整理可得

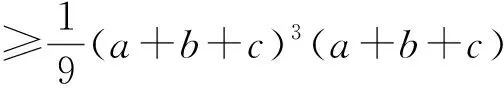
≥3abc(a+b+c)，

即不等式链(2)成立.从而命题不等式链(1)获证.

2017年12月号问题

(来稿请注明出处——编者)

2396形如n=16a(16b+15)(a,b∈N)的正整数不能表示成14个整数的四次方和.

(浙江省富阳二中 许康华 311400)

2397如图，四边形ABCD对角线相交于点O且AO=λOC．记∠ABO=∠1，∠ADO=∠2，∠CBO=∠3，∠CDO=∠4．求证：

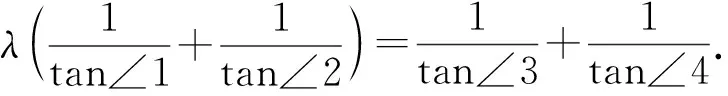
(重庆市长寿龙溪中学 吴 波 401249)

2398设a,b,c>0,a+b+c≤3,求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

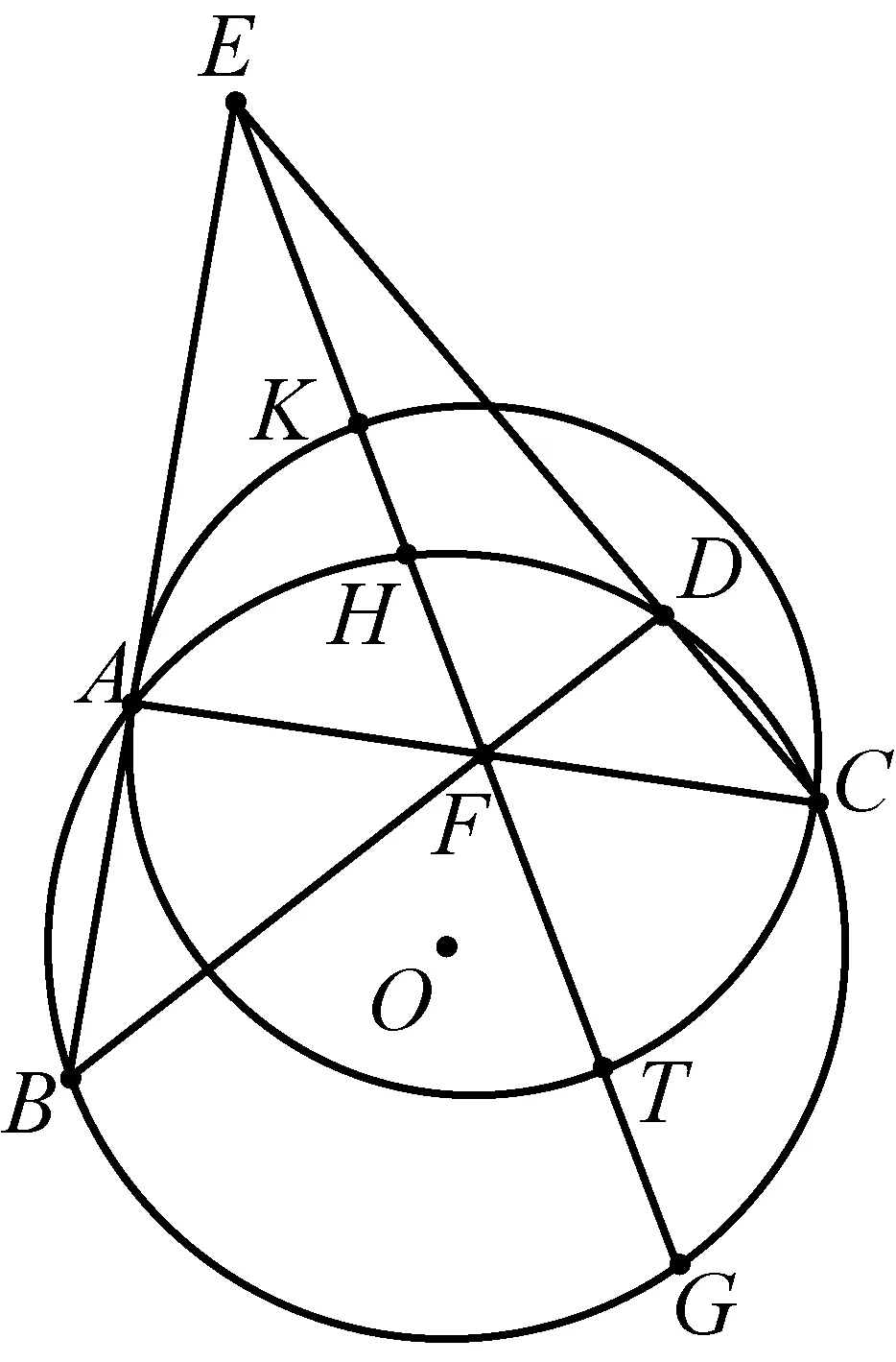
2399如图，已知⊙O上四点A、B、C、D，BA交CD于E，AC交BD于F，EF交⊙O于H、G，K为EF中点，以点A、K、C作圆交EG于T，求证：HF=TG.

(江西师范高等专科学校 王建荣 335000，温州私立第一实验学校 刘沙西 325000)

2400设△ABC中的三边长分别为a,b,c，外接圆和内切圆半径分别为R,r，求证：

(河南质量工程职业学院 李永利 467000)