关于位似概念的注记
胡志广 阿孜古丽·吉力力
(1. 天津师范大学数学科学学院 300387; 2. 新疆和田地区教育学院 848000 )
在中学,图形的相似和位似是两个教学内容.
定义1如果两个多边形满足对应角相等,对应边成比例,那么这两个多边形相似.
定义2两个多边形相似,而且对应顶点的连线相交于一点,对应边平行或共线,这样的两个图形叫做位似图形,这个点叫做位似中心.
关于位似图形,人教版就采用上面的定义方式.但不同教材给出的定义不尽相同,位似概念引起了很多老师的讨论([1-5]),甚至产生误解(可见[3]).本文,我们给出位似概念的常见误解剖析,并给出图形位似的常见等价形式:
定理下面陈述中,当图形都是多边形时,相互等价:
(1)两多边形位似,即它们相似,且对应顶点的连线相交于一点,对应边平行或共线.
(2)两图形相似且对应点的连线过一固定点.
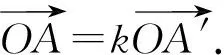
1 常见误解的剖析
(a)定理中的相似为“一种存在”,不一定与所给的相似相同.如图一,正方形ABCD与正方形GFEB相似,而在此对应下,对应顶点的连线没有公共交点.但这两个正方形位似,且有两个位似中心O和P.
图一
图二

图三
图四
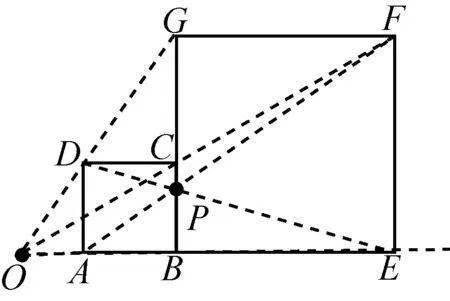
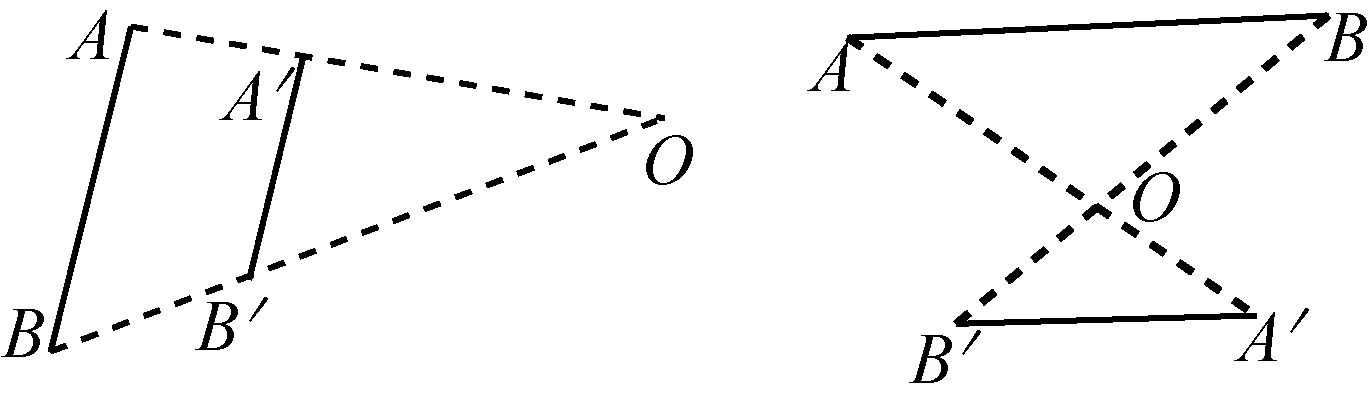
(b) 定理的(1)中的“对应边平行或共线”不可缺少.如图二,三角形ABC与ABD关于AB轴对称,它们全等,自然相似.显然它们有对应边不平行,故不位似.也可见[4]中的反例.
(c)定理的(1)中的“相似”不是多余条件.如图三,梯形ABEF与BCDE不位似.
(d)定理的(1)中的“对应顶点的连线相交于一点”不能少.如图四,三角形的平移不位似.
(e)定理的(2)中的对应点不能是“对应顶点”,与上(b)同.
(f)定理中的(3)之②的“向量”不能改成“线段”.如位似比为k和-k的图形组合.
2 定义等价的证明
(2)⟹(1)设AB和A′B′是不共线的对应边,假设AB和A′B′不平行,设交点为H.取AB和A′B′的中点C和C′,则它们是对应点,从而C、C′和O三点共线.由梅涅劳斯定理,用直线COC′分别截△AA′H和△BB′H,得
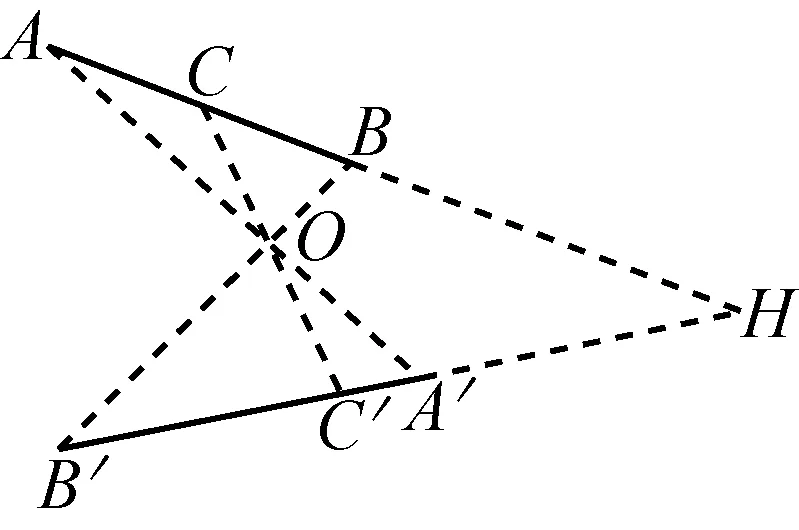
图五
这说明AB∥A′B′,矛盾.因此AB∥A′B′.

若AB∥A′B′,则如图六所示都有
图六
若AB和A′B′共线,分两种情况讨论.当点A、B均不等于点O,则顶点A和B所在的另一边ZA和BC分别平行于Z′A′和B′C′,于是
注意到kAB至少与kZA和kBC之一相等,不妨设kAB=kZA.于是
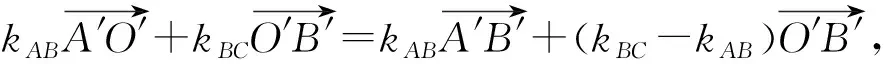
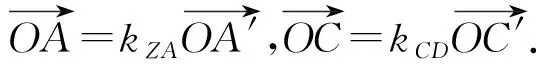
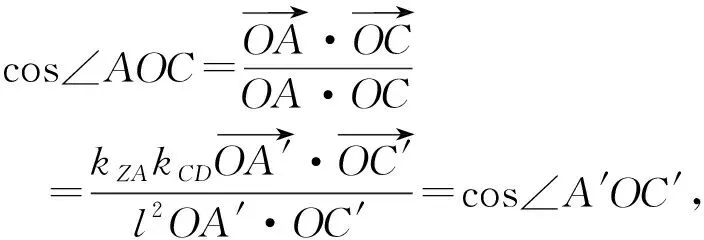
也得到kCD=kZA.
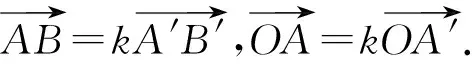
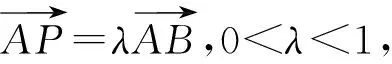
(3)⟹(2)我们先证明命题:在(3)的条件下, 边对应于边.
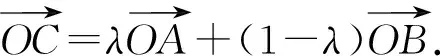
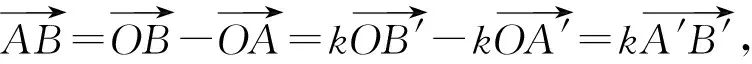
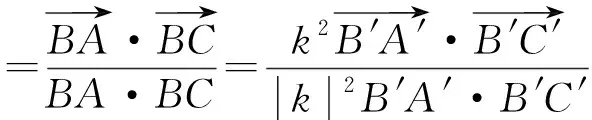
=cos∠A′B′C′,
可知对应角相等.因此两多边形相似.
3 图形位似的性质
(i)M1与M2位似,位似比为k1,M2与M3位似,位似比为k2,则当k1k2≠1时,M1与M3位似,位似比为k1k2;当k1k2=1时,M1与M3重合或相差一个平移.
设位似中心分别为O1和O2,在位似变化下,A1的像为A2,A2的像为A3,于是有
从而
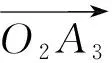
当k1k2≠1时,上式可变形为
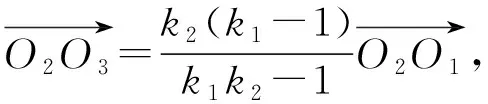
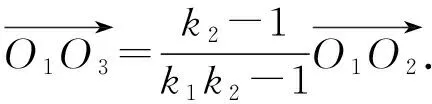
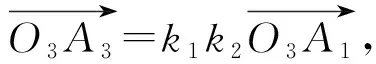
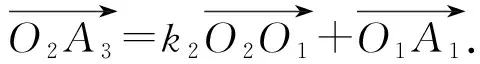
(ii) 两有界位似图形的位似中心至多有两个.并且有两个位似中心的多边形边数为偶数.
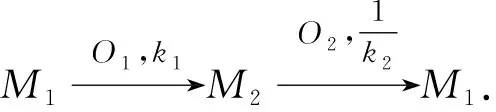
注:两平行线有无穷多个位似中心.

