高一学生关于平面概念的意象①

沈中宇 沈金兴

(1.华东师范大学数学系 200241; 2.浙江省桐乡市凤鸣高级中学 314500)

1 引言

“平面”是高中数学立体几何中学生正式接触到的第一个抽象概念.人教版《数学2》(必修)从生活情境引入平面，并利用生活中的实例引出平面的性质，这样的设计突出了平面的生活气息，但从生活中的平面抽象到数学中的平面，学生在对平面的进一步认识上存在障碍.在教学中，受希尔伯特几何公理体系的影响，平面概念是作为不加定义的原始概念出现的.于是，教师通常忽视此概念的教学以及学生的原有认识.

实际上，数学教育家早就认识到，人的头脑并不是一个单纯的逻辑实体，其内部复杂运行方式与单纯的数学逻辑不同，因此，我们必须区分正式定义的数学概念和它们在我们认知过程中所持有的形式.基于此原因，20世纪80年代初，D.Tall 和S.Vinner区分了概念定义和概念意象，概念意象是与某个概念相关的整个认知结构[1].概念意象包括关于这个概念的心理图像(概念的视觉表征和符号等)和与这个概念相关的性质.概念意象建立在个体的所有经历之上，随时间而变化，了解学生的概念意象对我们非常重要[2].S. Vinner后来又提出“获得概念就是形成概念意象”，所以形成好的概念意象，会对学生把握和运用概念有所帮助.但由于概念意象是建立在学生个体的所有经历之上，而不同个体的学习基础、思维加工方式与学习习惯会不同，使用的工具也可能各异，导致建立的意象可能完全不同.且即便是同一个体，也会随着时间的推移及学习经验的积累与深入，会对原有意象进行加工、调整、补充、修改、提炼等，会形成新的意象，从而使自己的意象越来越接近于概念本身.这进一步表明学生要真正构建起完整准确的概念根本离不开概念意象的帮助.因为它不仅可以让我们更好地了解学生，同时对我们的教学也有促进作用[3].

为了深入了解学生对平面概念所持的原有观念，克服学生学习平面的障碍，更好地进行教学，我们需要回答一下问题：未学过“平面”的学生对此概念持有什么样的意象？由此我们可以得到什么教学启示？

2 研究方法

2.1 样本的选取

问卷测试的对象来自于一所普通高中的高一学生共260名，他们的数学水平根据中考的数学成绩来看，呈正态分布.数学优秀生与较薄弱的学生各占20%，60%集中在中等程度，男女生比例比较接近，具体信息如表1.由于这些学生刚从初中升入高中不到一个月，因此对高中的数学知识还知之不多，基本上停留在初中所学的数学内容，故学生的头脑中还没有三维空间的立体感，只有二维的平面几何印象，很适合于了解学生关于立体几何中基本概念“平面”的原始意象是如何表征的.

表1 测试学生的数学水平与性别分布

为了进一步了解学生心中对“平面”究竟是怎么想的，在测试后又进行了访谈.共抽取11人作了访谈，其中男生5人，女生6人，数学水平按优秀、中等、薄弱分别为3人、6人、2人.

2.2 研究工具

问卷调查的测试题为：当你看到“平面”这两个字时，你会想到什么？把你想到的写在下面的横线上(已经画好6条横线)，有多少写多少，不够的可自行添加横线.

访谈的问题为“你写的这个内容是怎么想到？”，主要目的就是进一步了解学生内心的真实想法.

2.3 问卷调查与访谈的实施

问卷测试安排在自修课上进行，且全部有效回收.访谈安排在测试之后的一周进行，此时已统计好了所有学生的回答，并已分类.所以根据回答类型，分别选择了不同数学程度的学生.先给他们看当时自己的回答，然后再进行询问，对访谈过程全程录音并作记录，以供继续研究之用.

3 测试结果

3.1 问卷调查的结果

学生共给出了1110条回答，人均4.27条，其中最少的写出0条，最多的则写出了8条.这些回答可以分为以下7类：生活类、旧有知识类(简称旧知类)、图形类、物理属性类(简称物属类)、几何属性类(简称几属类)、关系类和想象类.

其中生活类是与生活中学生所遇到的平面原型相关的回答，旧知类是指与学生之前学过的数学知识相关的回答，图形类为与平面图形相关的回答，物属类是与生活中平面原型所具有的一些物理特征相关的回答，几属类是与平面的几何属性相关的回答，关系类是和平面与点、线、面和空间之间关系相关的回答，想象类是与平面概念距离较远的一些回答，图1给出各类意象出现频率的分布情况.

每位学生所持意象的丰富程度不同，最少的没有给出，最多的则给出了6类，平均每人写出2.83类，图2给出了各类别数的分布情况.

接下来对每类的具体情况进行描述.

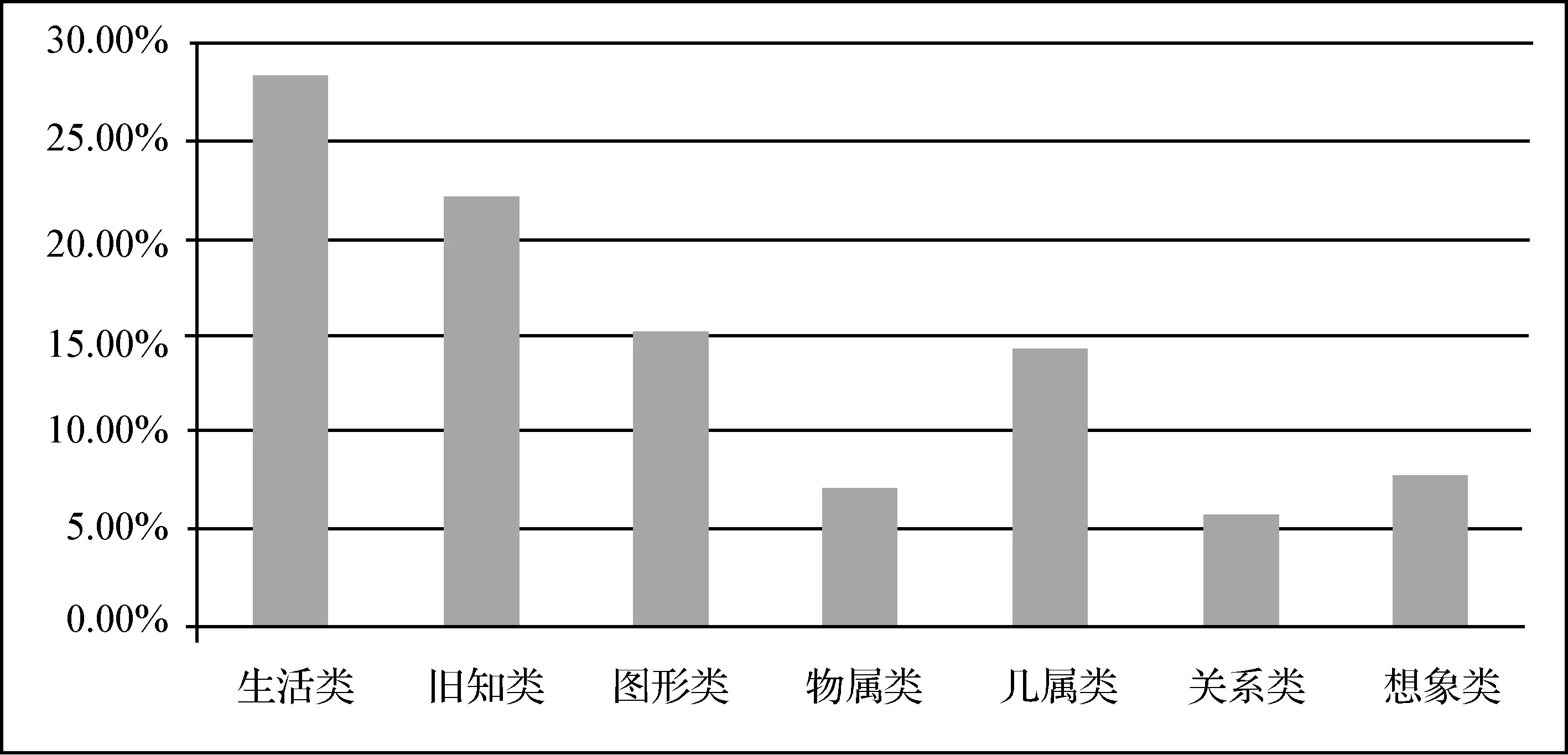
图1 不同回答类型的频率分布

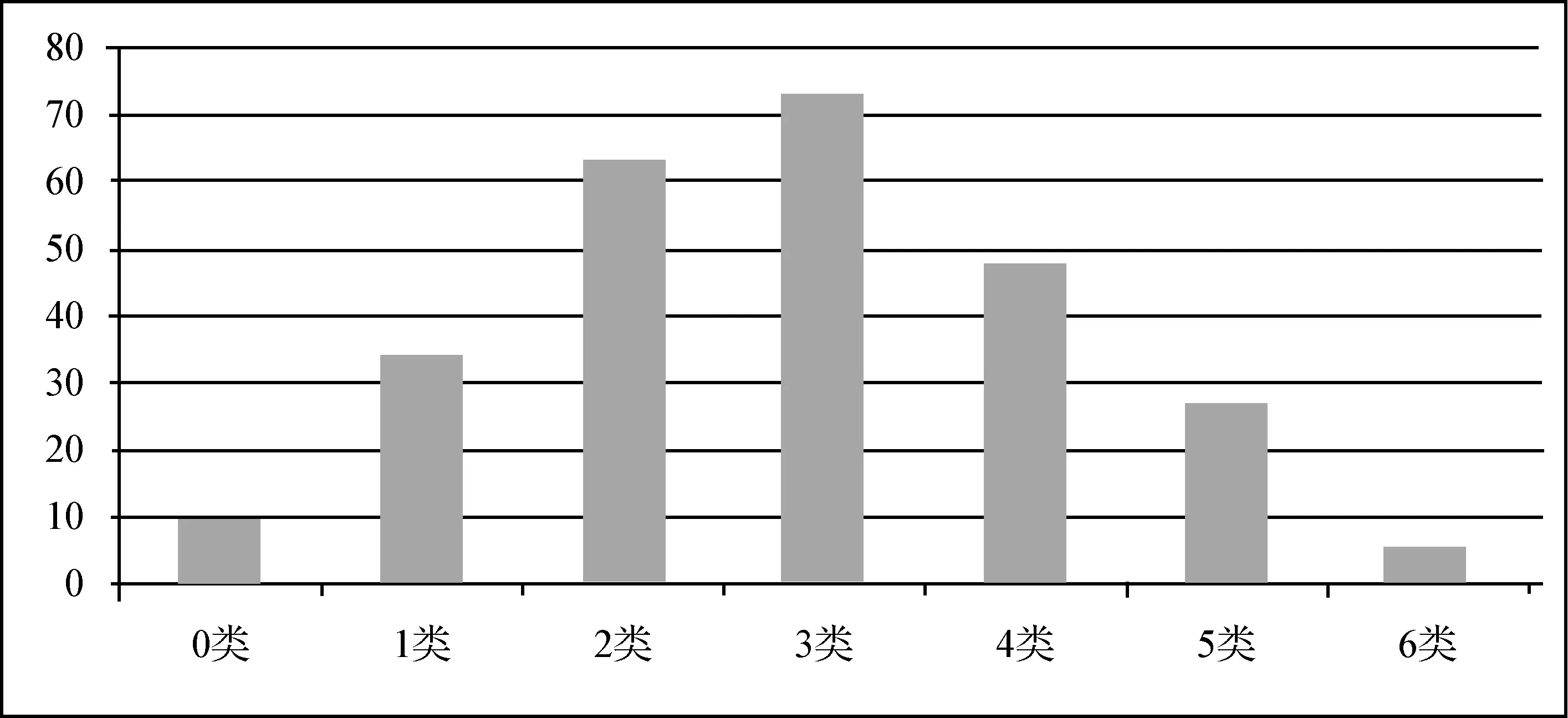
图2 各种类别的分布情况

3.1.1 生活类

生活类所占的频数是最多的，有313条(占28.20%).此类为生活中学生所遇到的平面原型，主要包含以下几种情况.

日常生活中常见的带有平面特征的物体(频数为216)：“桌面”、“地板”、“墙壁”、“地面”、“纸面”、“玻璃”、“黑板”、“平板电脑”等.

带有平面特征的自然景观(频数为73)：“海平面”、“河面”、“湖面”等.

比较特殊的例子(频数为24)：“银河系”、“动画”、“物体的某个面”、“物体与地面的接触面”、“图案”等.

3.1.2 旧知类

旧知类是所占频数第二多的类别，有244条(占21.98%).此类为学生之前学过的与平面相关的数学知识，可以分为平面几何的知识和代数的知识两大部分.

平面几何知识(频数为153)，其中占的比较多的回答是与平面相关的“点”、“线”以及平面几何中关于点和线的相关命题(频数为66).如“平面上两条直线与第三条直线平行，则这两条直线平行”、“过一点只有一条直线与另一条直线平行”等.其余还包括由平面的“平”字联想到的“平角”、“平行线”、“平面图”等，其中一个面为平面的立体几何图形如“立方体”、“多面体”等.其余还有“立体几何”、“三维空间”、“几何作图”等.

代数知识(频数为91)，其中所占较多的回答是“平面直角坐标系”，其次是由此联想到的“抛物线图象”、“函数图象”、“数轴”、“坐标轴”等.

3.1.3 图形类

图形类所占的频数也比较多，有168条(占15.14%)，此类中有直接回答为“平面图形”(频数为81)，也有写特殊的平面图形(频数为86)如“圆”、“三角形”、“长方形”等，还有直接画出平面图形(频数为1)的，如直接画个长方形在横线上.

3.1.4 物属类

物属类有78条(占7.03%)，在此类中，学生写出生活中平面原型所具有的一些物理特征.可以将其分为关于“平”的特征、关于“大小”的特征、关于“厚薄”的特征，每类的具体表现如下.

关于“平”的特征(频数为57)：“不能弯曲”、“没有弧度”、“平的”、“水平的面”、“光滑的面”、“没有起伏”、“扁平”等.

关于“大小”的特征(频数为7)：“很广”、“很大”、“无边际”、“任意方向”等.

关于“厚薄”的特征(频数为14)：“极薄”、“侧面看是一条线”等.

3.1.5 几属类

几何属性类有158条(占14.23%)，此类中，学生对平面的几何属性进行了一定的抽象刻画.可以将这些刻画分为4类，第一类是关于平面宏观几何性质的刻画，第二类是平面微观几何性质的刻画，第三类是对平面抽象性质的刻画、第四类是一些对平面性质的错误刻画.

关于平面宏观几何性质(28条)，这类性质包括平面的运动以及平面的上位概念，具体表现有：“旋转”、“平移”、“位置”、“一个面”、“表面”等.

关于平面微观几何性质(10条)，这类性质包括对平面构成的刻画，具体表现有：“由点组成”、“以点概面”、“点、线构成”等.

关于对平面抽象性质的刻画(110条)，包括了对平面无限延展性和无厚度两个特性上的认识，具体表现有：“二维”、“没有厚度”、 “非立体”、“没有长度”、“可延伸”等.

关于对平面性质的错误刻画(10条)，主要是没有对平面无限延展性这一特性的正确认识，具体表现有：“只有长和宽的面”、“封闭图形”、“限定范围”、“面积”、“不含点线”等.

3.1.6 关系类

关系类有63条(占5.68%)，主要是对平面与点、线、面和空间之间关系的描述与刻画.主要可以分为2类，第一类是对点、线、面之间的空间状态的描述，第二类是平面与点、线、面之间性质的描述.

对点、线、面之间的空间状态的描述(41条)包括：“平面与空间”、“同一空间”、“多个平面组成的空间”、“正方体的各面”、“平面与平面平行”、“平面与平面垂直”、“垂直于平面”、“直线与平面”、“平面与平面相交”等.

对平面与点、线、面之间性质的描述(22条)包括：“在同一平面上”、“不在同一平面上”、“确定一个平面”、“平行的线在同一平面上”、“同一平面上的直线相交或平行”、“直线所在的平面”等.

3.1.7 想象类

想象类有86条(占7.75%)，主要是对平面一些上层思考，或者与平面概念距离遥远通过想象得到的一些图像.主要可以分为3类，第一类是对平面的上层思考，第二类是与平面基本无关的图像，第三类是与平面的物理属性联想到的性质.

关于平面的上层思考(21条)，具体表现有：“只是一个概念”、“什么是平面”、“平面从何而来”、“没有真正意义的平面”、“抽象”、“数学”.

与平面字面相关(56条)，具体表现有：“平面游戏”、“平面模特”、“平面设计”、“分布”、“想象”、“空白”、“单调”、“乏味”、“数学题”、“三体”、“面条”等.

对平面物理属性的联想(9条)，具体表现有：“镜面反射”、“视线的范围”、“平抛的物体运动轨迹是抛物线”等.

3.2 访谈的结果

通过访谈，进一步了解到了学生心中的真实想法.对学生心中的“平面”意象原型归纳，主要来自于以下五类.第I类意象原型来自文字直观，如学生说：“因为有‘平面’这两个字，所以让我想到了平面直角坐标系、平面图形”等.第II类意象原型来自生活中类平面的物体，如桌面、墙面、黑板面，地面等，学生说：“这些都是我的生活中随时可见到的象平面的物体”.可见学生的实物意象也不是空穴来风，而是与学生密切相关的生活原型，因此学生整天生活着的空间，教室里的各种类平面物体就成了学生写得最多的.第III类意象原型来自兴趣爱好，如有一男生写了“魔方的一面”，问他怎么想到的，该生回答：“我喜欢玩魔方，就自然想到了”；再如一女生，她写了“平面模特、平面设计”，问她时说：“前面两个字‘平面’是由题中‘平面’两字想到的，后面的‘模特、设计’是因为平时自己喜欢看服装设计类的杂志，爱好这方面而想到的”.第Ⅳ类意象原型来自数学中的抽象，如“没有立体的画面”、“正方形”、“正方体的一个面”、“由线成面”等，当问到是何原因想到这些时，学生回答：“以前数学中学到的一些象平面的东西”.第Ⅴ类意象原型来自其他学科中的抽象，如“镜面反射”、“平坦的光滑面”等，学生说“平面无厚度，无凹凸，让人想到物理中的光滑面”.

访谈中表现出来的学生对平面意象的原型，完全依赖于学生各自体验到的客观物体或学过的学科知识经验，它的表征形式也与个人经历息息相关，包括学生的兴趣特长和爱好，同时也验证了辨证唯物主义中的哲学观点：“物质决定意识，意识是客观事物的主观反映”.所有这些也为平面教学带来某些启示.

4 结果分析

4.1 学生对平面认识的初步分析

从以上结果可以发现，生活类、旧知类和图形类是学生持有最多的前三个意象，占到总条数的65.32%，因此可以看出学生对于平面概念的意象主要有两个来源，一方面来自于生活实践，对应的是生活类.另一方面来源于之前所学的数学知识，对应的是旧知类和图形类.其中生活类中出现最多的还是学生日常生活中接触到的物体，旧知类中出现较多的是平面几何中的知识.图形类则说明了学生对于平面的心理图形基本上是一些具体的图形.通过访谈部分学生，得知学生填写最多的这三个意象是由于受到了“平面”这两个字以及日常生活的启发，而物属类、几属类、关系类则主要来源于学生的抽象思维.

从图2可知：三江平原北部平原地区的径流深小于100.0 mm(多年平均降水量的17.5%)，大部分地区小于75.0 mm(多年平均降水量的13.2%)。根据表1，安邦河、挠力河、同抚和萝北地区多年平均降水量为574.0 mm,按最小值521.7 mm计算，至少有446.7 mm的降水处于蒸发和渗漏状态。通常降水期间渗漏量是大于蒸发量的；再者图2是根据蓄满产流模型计算的，因此，该地区的入渗降水量应当大于230.0 mm。

物理属性类中出现最多的是学生对于平面中“平”的特征的描述，说明这一特征在学生心目中主要体现在生活中出现的各种与“平”相关的语言中，如平坦、没有起伏等.

几何属性也是学生中出现较多的一种回答，其中学生对于平面属性认识比较清楚的是它没有厚薄的特性，“二维”这个词出现的比较频繁，说明学生对于平面没有厚度这一特性认识的比较准备，而对于另一个无限延展的属性，认识到的学生则相对较少，甚至出现了平面具有大小、封闭图形等错误的认识，这可能受到了学生之前将平面对应为具体图形的影响.

对于关系类的描述相对较少，其中比较多的体现在学生将平面与空间进行对比，将平面作为立体图形的一个面上，这也与学生之前学过的一些简单几何体有关.

想象类的描述则出乎意料的相对较多，说明高中生也具有一定的想象能力，对于没有学过平面概念的学生，他们的答案并不一定是常规的，其中值得注意的是，有一部分同学对于平面概念具有一些元认知的属性，能思考平面到底是什么，平面从何而来等具有哲学意义上的问题.

4.2 学生对平面概念的历史相似性

平面的概念在历史上经过了漫长的发展，早在公元前5世纪，古希腊哲学家巴门尼德(Parmenides)对平面概念就已作过刻画[4]，在这之后，欧几里得(Euclid, 前3世纪)、古希腊数学家海伦(Heron, 约公元1世纪)、英国数学家辛松(R. Simson, 1687～1768)、法国数学家傅里叶(B. J. Fourier, 1768～1830)、德国数学家莱布尼兹(G.W.Leibniz, 1646～1710)、德国数学家希尔伯特(D.Hilbert, 1862～1943)等都对平面概念作过刻画.

巴门尼德将平面定义为“一个二维对象、直的表面”，欧几里得将平面定义为“与其上直线一样平放着的面”，海伦将平面定义为“平面是具有以下性质的面，它向四周无限延伸，平面上的直线都与之相合，且若一条直线上有两点与之相合，则整条直线在任意位置与之相合.”，辛松的定义与海伦的类似，傅里叶对平面的定义为“平面由经过直线上一点且与直线垂直的所有直线构成”，莱布尼兹将平面看成“平面是与两点等距离的点的集合”，希尔伯特将平面作为不加定义的量.

已有研究表明，非数学专业的毕业生，如社会学家、小学老师等工作人员对平面的理解具有历史相似性[5]，如表2所示，根据本次测试来看，发现了未学过平面概念的学生对平面的概念意象与历史上这些数学家想法也非常相似，具有显著的历史相似性.

表2 学生对“平面”概念的历史相似性

4.3 学生对平面概念的认知发展水平

从学生的平面概念意象可见，抽象程度和处理相关线索的能力有鲜明的层次性，因此，可以利用SOLO分类法[6]将学生对平面概念的认知划分为五个水平：前结构水平、单一结构水平、多元结构水平、关联结构水平和拓展的抽象水平，前结构水平(P)指学习者被情景中的无关方面所迷惑和误导，为以前所学的无关知识所困扰，对应的是想象类中很多无关的想象以及旧知类中以前所学的无关知识.单一结构水平(U)指的是学生关注主题或问题，但只使用一个相关的线索，对应的是生活类、物属类和图形类，学生提取的线索分别为生活情境、物理属性和图形表征.多元结构水平(M)指的是学生使用多个线索，却不能觉察到这些线索之间的联系，对应的是几属类，在此类中学生觉察到了一些相关的特征，如二维、点线构成等，但还较为零散，缺乏有机整合的能力.关联水平(R)指的是学生能将线索编入总体框架中，对应的是关系类，此类中，学生已经可以系统的思考点、线、面与平面之间的位置关系，具有一定的整体结构.拓展的抽象水平(E)代表一种更高水平的学习能力，代表学生有更强的钻研精神和创造意识，对应想象类中的关于平面的上层思考，这一类中学生认识到平面是一个概念、平面在现实生活中并不存在，概括考虑了新的和更抽象的特征.据此，可以将学生对平面的七类概念意象根据不同的抽象水平对应如表3所示.

表3 学生对“平面”概念的认知水平与概念意象的对应

实际上这五个层次的划分和平面概念的历史发展也是类似的，人类认识平面也是从生活中的具体实物以及具体图形出发，巴门尼德、欧几里得等将平面概念的“没有厚度”、“无限延展性”等核心性质突出出来，达到了较高的认知水平，经过历史的发展，最后由希尔伯特建立几何公理体系，从而将平面作为不加定义的量，用公理即各概念之间关系进行刻画，平面概念的抽象程度得到了的进一步提升.

将上述五个认知水平由低到高依次对应于水平0、水平1、水平2、水平3和水平4，并记为L0，L1，L2，L3，L4.表4给出了各水平的分布情况.

表4 学生关于平面的认知水平

用ni(i=0,1,2,3,4)表示各水平的频数，相应的权重di(i=0,1,2,3,4)依次为0，1，2，3，4，则运用公式

5 结论与启示

以上我们可以看到，在学生学习平面概念之前，高中生关于平面的概念意象可分为生活、旧知、图形、物属类、几属类、关系和想象7类，每位学生平均持有的意象为2.83类，学生基本能写出3类及以上的意象.学生的概念意象基本来源于生活与之前的教学，从某种意义上看，可以发现其中的历史相似性比较突出，而且基本可以将这些意象按照SOLO分类法分为几个认知水平，这与历史上平面概念的发展阶段也是类似的，并且高一学生对平面概念的认知水平中等偏下，因此我们可以得到的教学启示有以下几个方面.

首先，在学习平面概念之前，学生在生活以及之前的学习中接触了很多平面的原型，所以平面概念的教学可以建立在生活以及旧有知识的基础上进行，但也需要注意的是生活中形成的一些观念对平面概念的进一步学习具有阻碍作用，其中尤其要注意的是学生容易将生活中平面原型具有面积、固定范围这一特点迁移到学习中，阻碍平面无限延展性的学习.在引入生活实例的时候可以让学生提取其中的关键属性如“平”、“很薄”、“很广”，为之后进一步的抽象做准备，也可以让学生从学过的一些简单立体图形中体会平面的概念.

其次，由于学生对平面概念的意象具有丰富的历史相似性，所以可以考虑融入数学史的角度进行教学，将学生的理解与历史上数学家的思想相对应，可以让学生感受到概念的由来，知道一个概念不是凭空掉下来在教科书中出现的，而是经过几千年的演化而来，同时也增强了学生的数学自信，他们的想法与历史上数学家的想法一致.

最后，荷兰的著名数学教育家弗赖登塔尔说过：“与其让学生学习公理体系，不如让学生学习公理化……一句话，与其让学生学习数学，不如让学生学习数学化”[7].从学生关于平面概念的意象中我们可以看到学生不同层次的认知水平，这也是对平面概念进行数学化的过程，从中也可以感受到与平面概念历史发展惊人的相似，故可在已有的数学认知基础上安排教学，这就给我们的教学设计提供了参考，可以对平面概念的历史发展阶段进行重构，融入到我们的教学过程中，注重学生的自主探究和数学化的过程，从而真正实现学生对平面概念的深入理解，同时也获得宝贵的数学活动经验与能力.