一个新的三角形面积公式
曹嘉兴
(浙江省开化县第二中学 324300)
已知△ABC的三边长a、b、c求其面积△有我国南宋时期著名数学家秦九韶(1202—1261)在《数书九章》(1247)中提出的三斜求积公式:
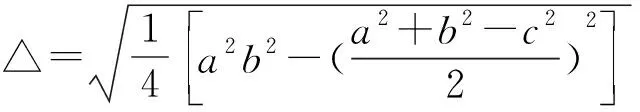
以及古希腊著名数学家海伦(Heron,约公元1世纪)在《测量学》(Metrica)一书中提出的公式:
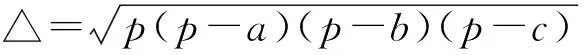
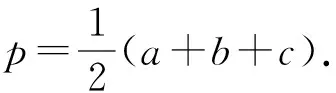
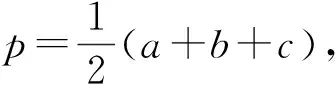
证明设△ABC的内切圆半径为r,
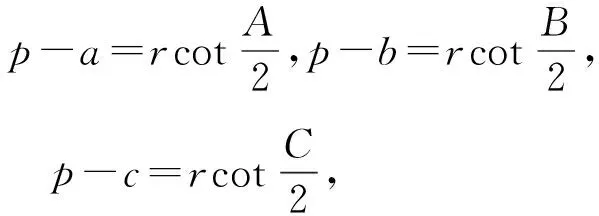
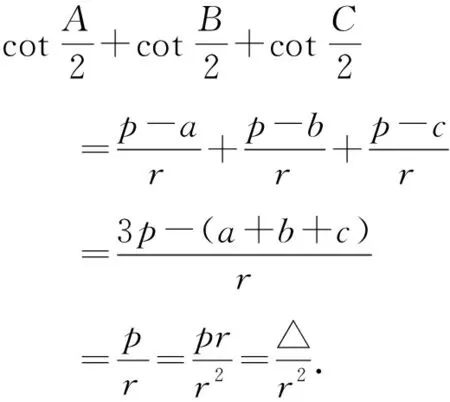
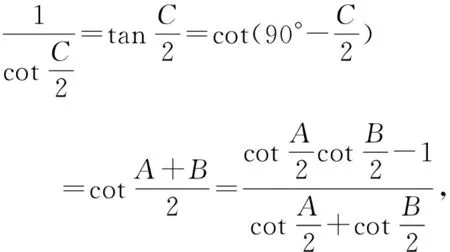
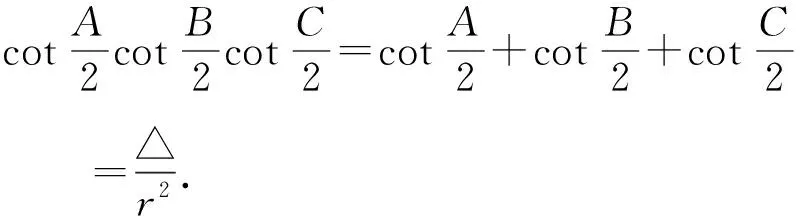
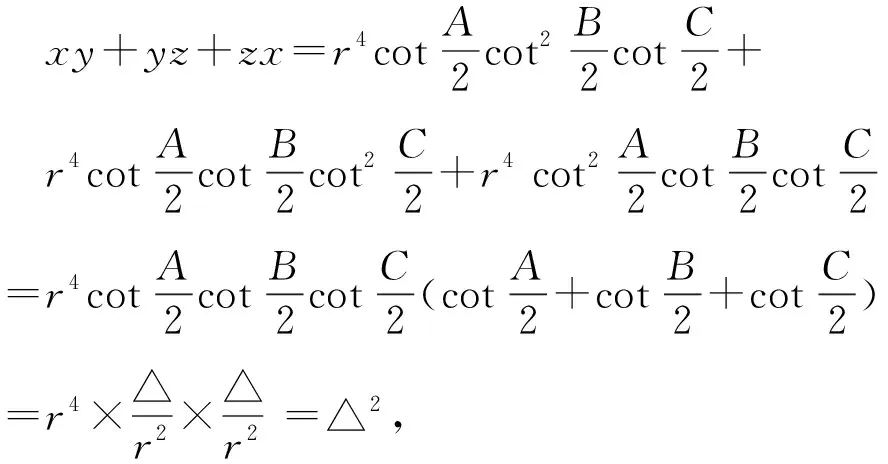
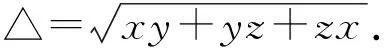
推论如图1, 在△ABC中,它的内切圆⊙O与各边AB、BC、CA分别相切于点D、E、F,设AD·DB=x,BE·EC=y,CF·FA=z,则△ABC的面积为
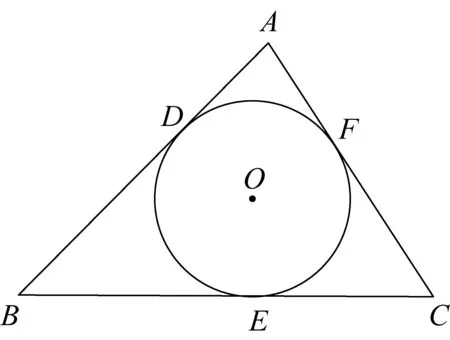
图1
容易验证本文给出的三角形面积公式与海伦公式也是等价的.事实上,
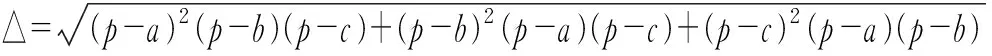
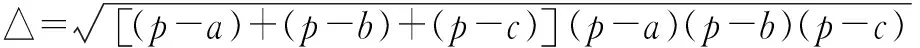
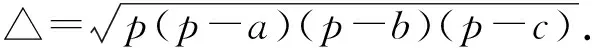
本文给出的三角形面积公式同样具有结构对称的形式,因此显得优美. 在一些场合还能简化计算(或证明)的过程,现举两例说明.
例1(Finsler―Hadwiger不等式)设△ABC的各边长分别为a、b、c,它的面积为△,则
当且仅当△ABC为正三角形时等号成立.
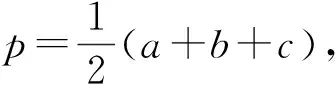
(p-a)(p-b)=x,(p-b)(p-c)=y,
(p-c)(p-a)=z,
则a2-(b-c)2=4y,b2-(c-a)2=4z,
所以原不等式等价于
[a2-(b-c)2]+[b2-(c-a)2]+[c2-(a-b)2]
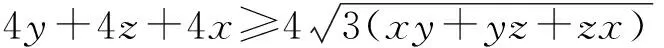
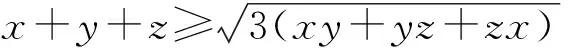
⟺(x+y+z)2≥3(xy+yz+zx)
⟺x2+y2+z2≥xy+yz+zx
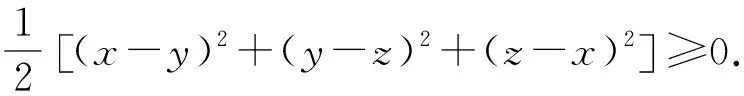
最后的一个不等式显然成立,故原不等式成立.
由最后的不等式不难看出当且仅当x=y=z,也就是p-a=p-b=p-c,即a=b=c时等号成立,故当且仅当△ABC为正三角形时等号成立.
例2(Goldner不等式)设△ABC的各边长分别为a、b、c,它的面积为△,则a4+b4+c4≥16△2,当且仅当△ABC为正三角形时等号成立.
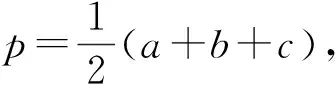
(p-a)(p-b)=x,(p-b)(p-c)=y,
(p-c)(p-a)=z,
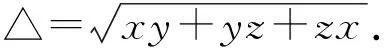

所以a4≥16(p-b)2(p-c)2=16y2,
同理可得b4≥16z2,c4≥16x2.
所以a4+b4+c4≥16(x2+y2+z2)
≥16(xy+yz+zx)=16△2.
由上述证明过程不难看出当且仅当p-a=p-b=p-c,即a=b=c时等号成立,故当且仅当△ABC为正三角形时等号成立.

