出租车几何学
——一种有趣的几何学
范逸璇
(吉林大学数学学院 130012)
1 出租车几何学
我们熟悉的初等几何学是以欧几里德(Euclidean)几何原本内容为基础而建构出来的.但是在真实生活中,受制于纵横交错之街道(如,纽约曼哈顿街道),两点之间很少能以直线行进方式到达,多数是以「前后左右」的方式行进,这使得原本的两点距离公式必须改写.
「出租车几何学」(Taxicab Geometry) 或「格子点几何学、曼哈顿几何学」.出租车几何学主要探讨在纵横交错街道的限制之下的几何系统理论基础,它是由生于俄国的著名德籍数学家闵可夫斯基(Hermann Minkowski,1864—1909)最先开始研究的.近年也有「校车几何」School-bus geometry(Cynthia Lanius,1998),初期并未正式架构出完整的理论基础,直到1975 ,Krause,Eugene F.才将Taxicab Geometry 做了进一步研究.本研究即以「出租车几何学」(Taxicab Geometry),表示一个路线仅能以「水平」或「铅垂」方向行进的坐标平面几何系统[1].
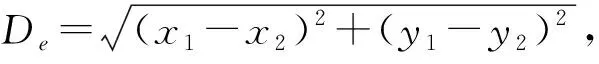
这是一个对“距离”的合理定义,因为它满足:
(1)非负性:两点距离总是大于等于 0 ;
(2)对称性:A到B的距离等于B到A的距离;
(3)零距离:A到B的距离为 0 当且仅当A=B;
(4)三角形不等式:对于任意三点A、B、C,不等式AB+BC≥AC总成立.
也就是说出租车几何学是建立在一个合理的度量空间上的.这是一个全新的几何世界.
2 出租车几何—三角形性质
(1)在出租车几何学系统里,很多经典几何定理仍然成立.
①三角形的内角和还是180度.因为,这是一个关于角度的定理,与距离的度量方式无关;既然角度的度量方式不变,三角形的内角和也仍然不会变.
②两点间的最短路线有很多条.
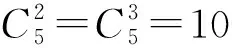

图1
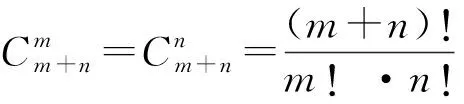
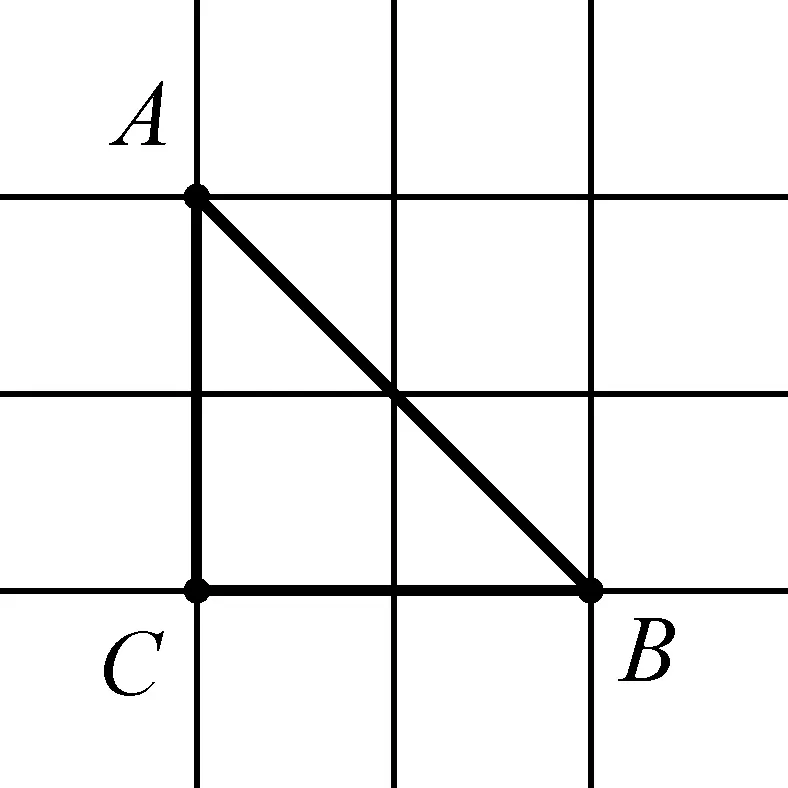
图2
(2)如果涉及到三角形的边长,很多命题就不再成立了.
①在直角△ABC中,勾股定理不成立.另一结论:斜边等于两直角边之和:AB=BC+CA.
如图2,在直角△ABC中,设A(x1,y1)、B(x2,y2)、C(x1,y2),根据出租车几何学距离(两点之距离)公式:AB=|x1-x2|+|y1-y2|,AC=|x1-x1|+|y1-y2|=|y1-y2|,BC=|x1-x2|+|y2-y2|=|x1-x2|,即AB=BC+CA.
②“等边对等角”、“等角对等边”不成立.例如图3中的△ABC,虽然AB=AC=3,但∠B≠∠C.在△MNS中,虽然∠N=∠S(=71.57°),但MN=5,MS=7.
在出租车几何中,还能画出等边直角三角形(图3,△PQR).

图3
③在出租车几何学中,不能用“边边边”判断三角形全等.
我们画出两个△ABC、△A′B′C′,它们的对应边都相等(AB=A′B′=2,BC=B′C′=4,AC=A′C′=6),但这两个三角形并不能重合在一起.
④在出租车几何中,不能用“边角边”判断三角形全等.
如图4中,在直角△GHF、△G′H′F′中,GH=G′H′,FH=F′H′,但是它们不全等.
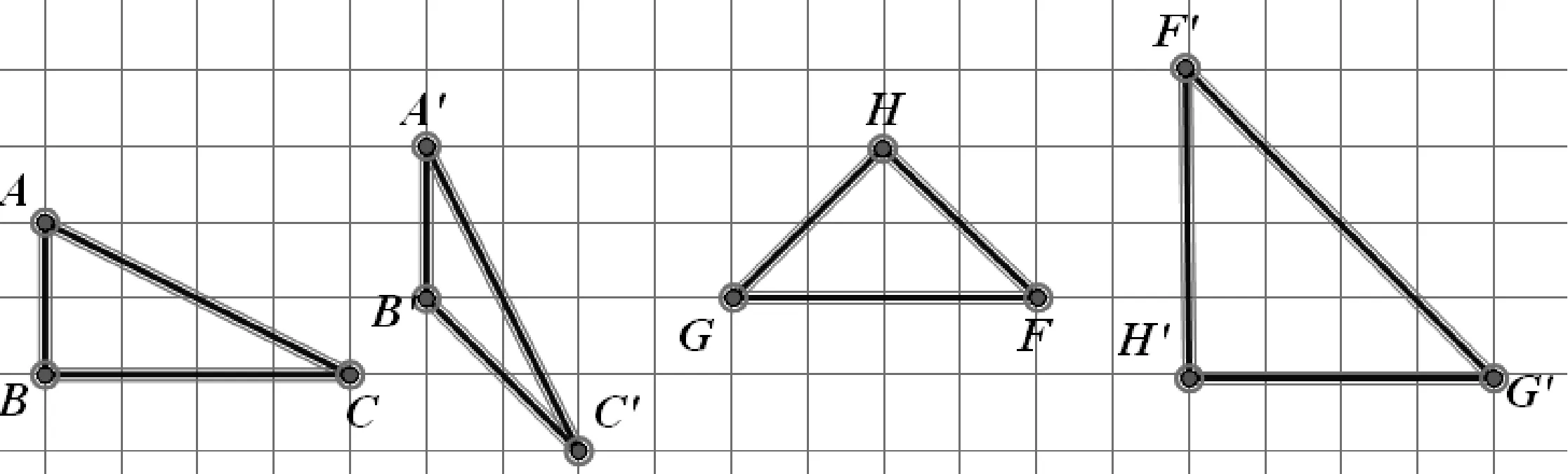
图4
3 出租车几何学系统中的「圆」
圆是到某个定点等距离的点集合.在欧几里德几何系统中,假设定点为O(a,b),与O点相距r之点集合为{(x,y)|(x-a)2+(y-b)2=r2},它的图形是圆.
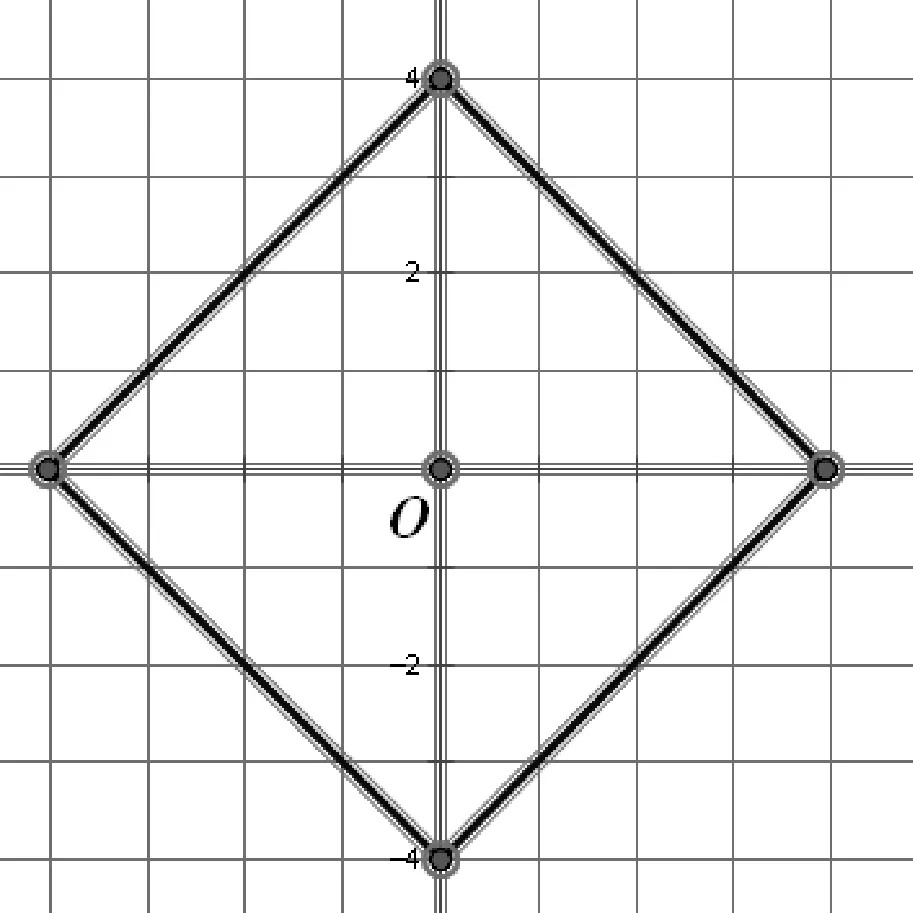
图5
而在出租车几何系统中,与定点O距离r的点集合为{(x,y)||x-a|+|y-b|=r},它的图形是以O(a,b)为中心的「正方形」,如图5.
在出租车几何系统中,半径为正整数r的圆都是由4r个点组成的图形,且其圆的周长为8r.
「圆」的周长与直径之比值为此系统的「圆周率」.「圆周率」为8r÷2r=4.
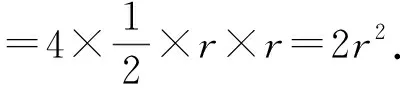
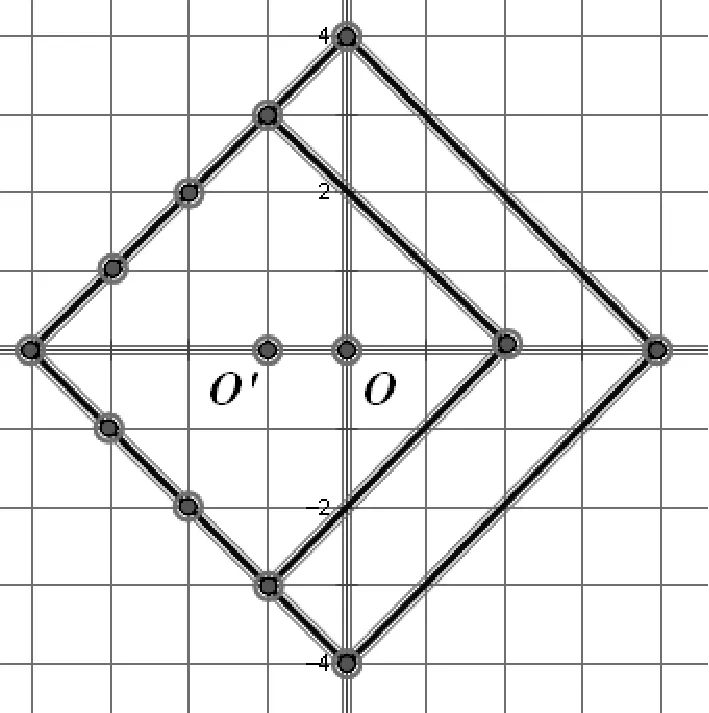
图6
在欧几里德几何学中,两个圆的公共点不超过两个.而在出租车几何学中,两个圆的交点可以有多个,例如(如图6),半径为3的圆O′与半径为4的圆O有7个交点.
4 出租车几何学系统中之「中垂线」
在欧几里德几何系统中,「与两定点距离相等的点集合」的图形为连接两定点线段的中垂线,但是按照此定义,在出租车几何学系统中,「与两定点距离相等的点集合」,却不是大家熟悉的「中垂线」,因此姑且称之为「等距线」.
在出租车几何学系统中,两定点坐标A(x1,y1)、B(x2,y2),与A、B两点等距离的点集合为|x-x1|+|y-y1|=|x-x2|+|y-y2|的解.重新定义距离后,很多图形会变得更加复杂.定义两点间的垂直平分线为到两点距离相等的点组成的图形.在这个几何世界里,垂直平分线是什么样的?在一般情况下,垂直平分线并不一定是“垂直”平分线,而可以是一条折线段或其他情形.
问题[2]在出租车几何学系统中,在J(-6,-1)、F(-3,3)、R(2,1)三个楼盘之间建设一所学校S,要求SJ=SF=SR,如何确定S点(三条“中垂线”交点).
(1)|SJ|=|SF|,|x+6|+|y+1|=|x+3|+|y-3|
(※1)
①当-1≤y≤3和-6≤x≤-3,
(※1)变为:x+6+y+1=-x-3-y+3,即y=-x-7/2.
②当-1≤y≤3和x<-6,
(※1)变为:-x-6+y+1=-x-3-y+3,即y=5/2
③-1≤y≤3和x>-3,
(※1)变为:x+6+y+1=x+3-y+3,即y=-1/2
参见图7中的粗实线.

图7
(2)|SF|=|SR|,|x+3|+|y-3|=|x-2|+|y-1|
(※2)
①当1≤y≤3和-3≤x≤2
(※2)变为:x+3-y+3=-x+2+y-1,即y=x+5/2
②当x<-3 和y<1,
(※2)变为:-x-3-y+3=-x+2-y+1
-x-y=-x-y+3,由于 0≠3,在x<-3和y<1条件下无解.
③当-3 ≤x≤2 和y<1,
(※2)变为:x+3-y+3=-x+2-y+1,即x=-3/2
④当-3 ≤x≤2 和y≥3,
(※2)变为:x+3+y-3=-x+2+y-1,即x=1/2
参见图7中的细实线.
(3)|SJ|=|SR|,|x+6|+|y+1|=|x-2|+|y-1|
(※3)
①当-6 ≤x≤2 和y<-1,
(※3)变为:x+6-y-1=-x+2-y+1,即x=-1
②-6 ≤x≤2和-1 ≤y≤-1,
(※3)变为:x+6+y+1=-x+2-y+1,即y=-x-2
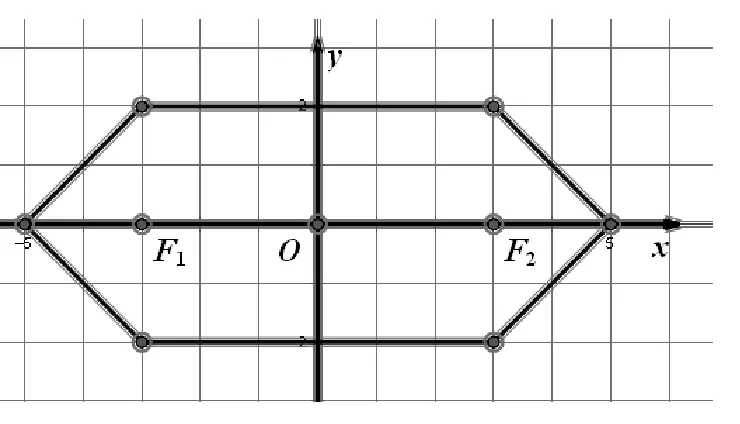
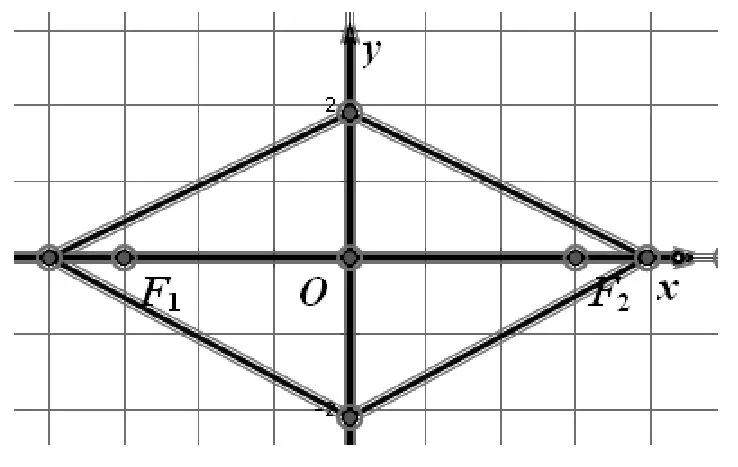
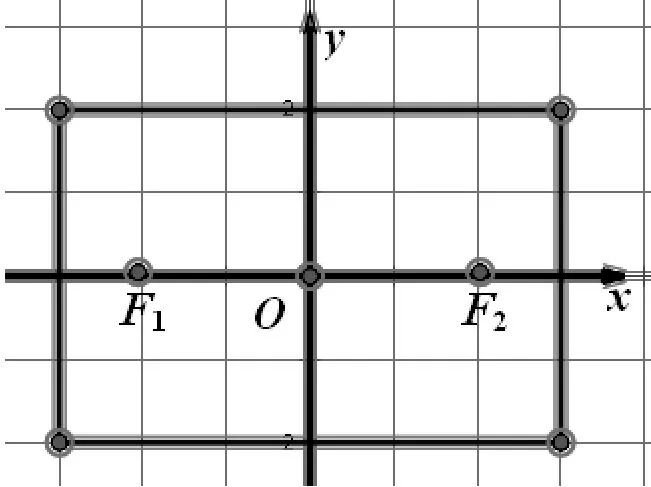
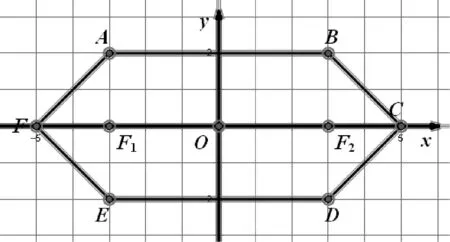
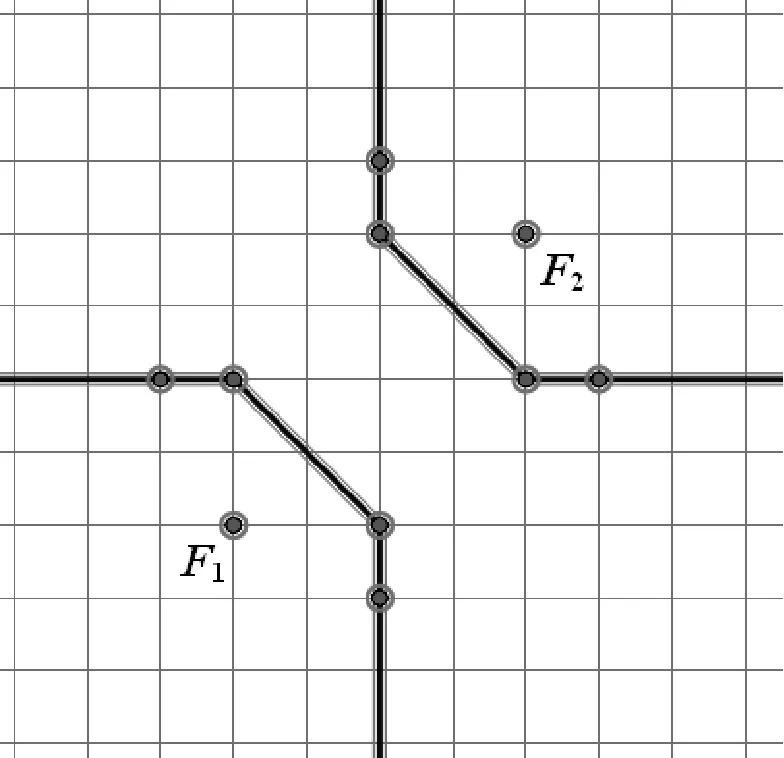
③-6 ≤x≤2和1 (※3)变为:x+6+y+1=-x+2+y-1,即x=-3 参见图7中的虚线. 三条线交点(-1.5,-0.5)为所求S点.图8中正方形(点虚线)为JFR三点的“外接圆”. 尽管垂直平分线如此奇怪,不过(一般情况下)三角形三边的垂直平分线仍然交于一点.这个点也是名副其实的“外心”,以它为中心可以作出这个三角形的“外接圆”. 图8 还有一些特殊的情况,出租车几何系统中三点不仅仅确定一个圆.例如,同时过A(0,1)、B(0,-1)、C(1,0)的圆就有无穷多个(如图9).这是因为:A(0,1)和C(1,0) 的垂直平分线是∠BCO区域中(包括边)各个网格线的交点,如点P(它到点A和点C的距离都是7);同理B(0,-1)和C(1,0) 的垂直平分线是∠ACO区域中(包括边)各个网格线的交点.这两个区域的交点(坐标轴上的点)O、O1、O2、O3、O4、…就是点A、C、B的外接圆的圆心,对应半径分别为1、2、3、4、5、…,如图9,得到对应的若干个圆. 图9 在出租车几何系统中,点到直线最短的距离为横向或纵向距离(与直线之斜率有关).点P(x1,y1)到L:y=mx+b的距离[3]: d=|y1-mx1-b|,-1 (1)对于定点P与直线L,任何到P点与L等距离之点所成的集合,在欧几里德几何系统中的图形为拋物线,但是在出租车几何系统中的图形又是什么呢? 图10 如图11. 图11 (2)直角坐标系x轴两个固定点F1(-c,0),F2(c,0),另外两个点F(-a,0),C(a,0) ,a>c>0 .则出租车几何系统的「椭圆」方程为 |x-(-c)|+|y|+|x-c|+|y|=2a 如图12. 图12 (3)直角坐标系x轴有两个固定点 F1(-c,0),F2(c,0),A1(-a,0),A2(a,0) ,c>a>0 .则出租车几何系统之「双曲线」方程为 |||x-(-c)|+|y||-||x-c|+|y|||=2a 图13 图14 还有更复杂的情形[4],如图14:焦点轴斜率为1的情形(它上面的点到两个定点(即焦点)A,B的距离之差的绝对值都等于常数4.),方程较复杂,略. 高考题 (2014·福建·文·12):在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为‖P1P2‖=|x1-x2|+|y1-y2|,则平面内与x轴上两个不同的定点F1,F2的“L-距离”之和等于定值(大于‖F1F2‖)的点的轨迹可以是( ) [答案A.] A B C D 与此具有相同背景还有福建2006高考题(理·12)、广东2010高考题(理·21).这三道高考题的背景都是出租车几何学.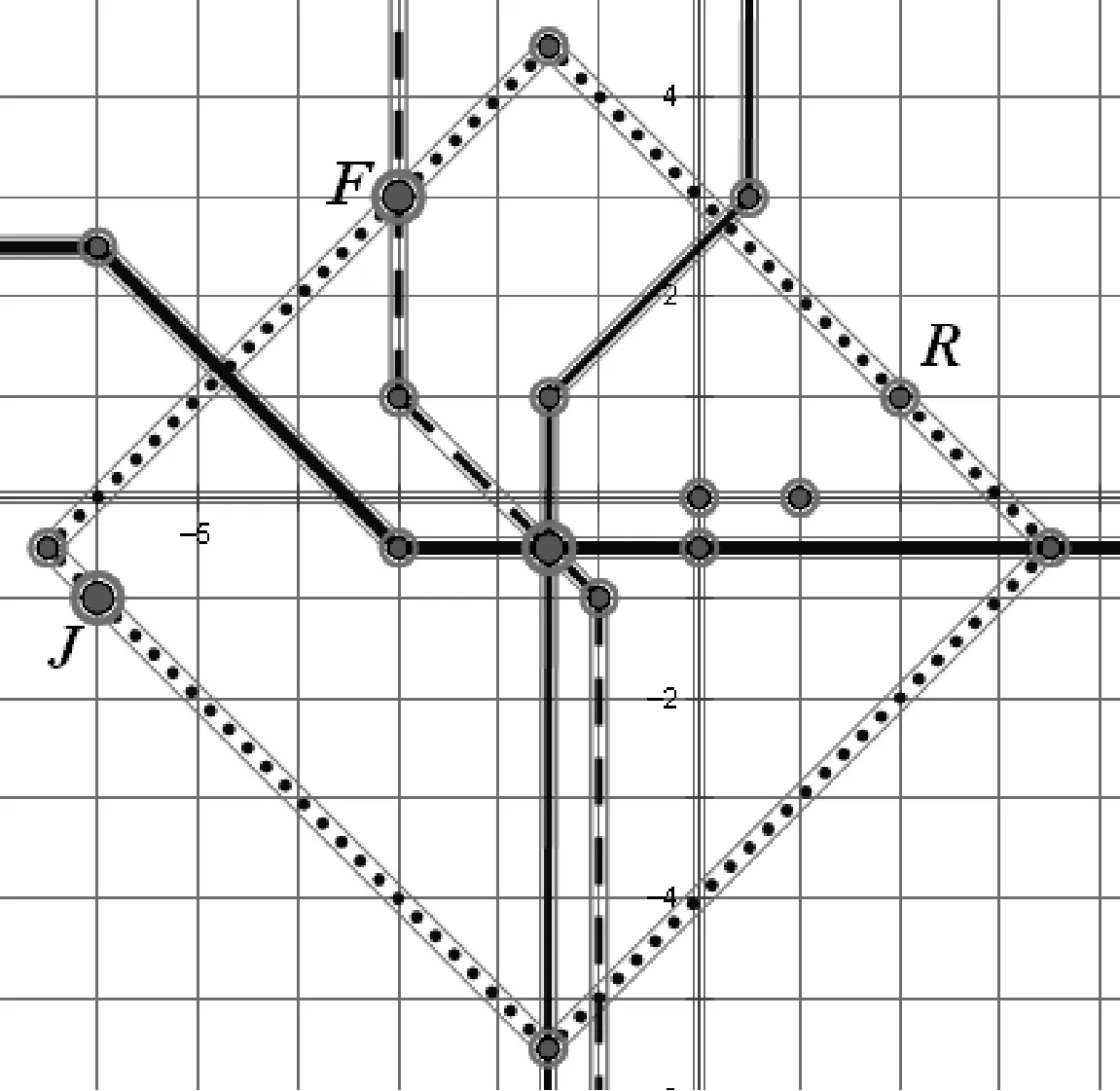
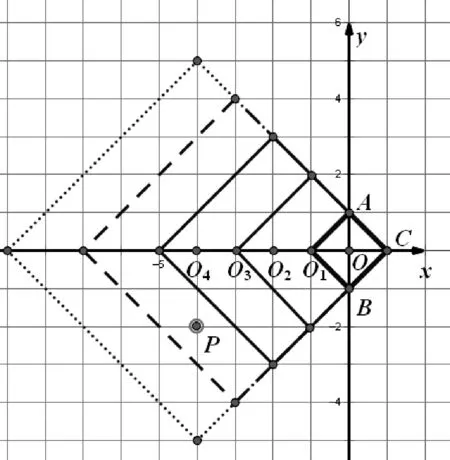
5 在出租车几何系统中,点到直线的距离例示
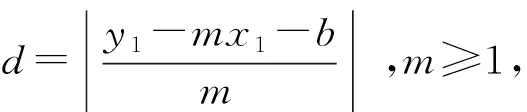
6 出租车几何学系统中的「圆锥曲线」
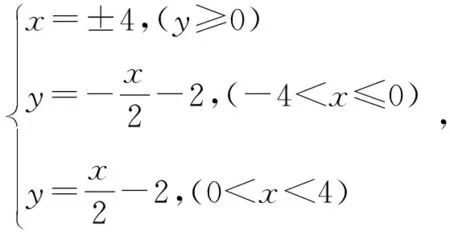
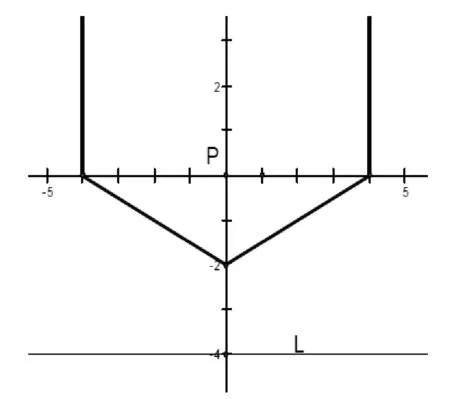



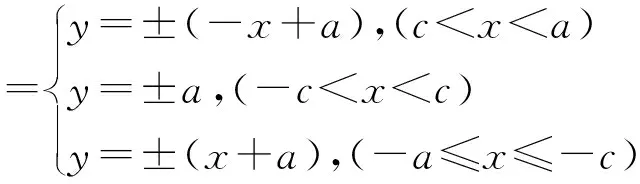

7 出租车几何背景的高考题