基于余弦7倍角公式求几个一元三次方程的解及其应用

黄盛清

(西南交通大学 610031)

《数学通报》 2015 年 10 月号问题 2268：

试证明

(1)

对该问题，问题提供人柳冉在《数学通报》2015 年第 11 期 “2015 年10 月号问题解答”[1]中反复利用正弦、余弦的积化和差等公式及一定的运算技巧给出了证明.

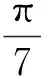
1 由余弦7倍角公式得到一个一元七次方程的解

余弦7倍角公式为

cos7θ=64cos7θ-112 cos5θ+56cos3θ-

7cosθ

(2)

令x=cosθ，a= cos7θ=cosφ，则式(2)可变形为

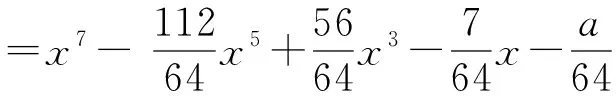
定理1方程fa(x)= 0的解为

证明因为a=cosφ=cos(2π±φ)

=cos(4π±φ)=cos(6π±φ)，

所以据式(2)定理1得证.

推论1取a=-1，则方程

的解为

证明a=-1，即 cosφ=-1，故可取φ=π，则由定理1 得推论1.

2 几个一元三次方程的解

将f-1(x)变形为

(3)

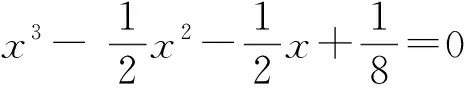
证明(a) 由式(3)，根据推论1即可证明此结论.

则由结论1(a)即可证明此结论.

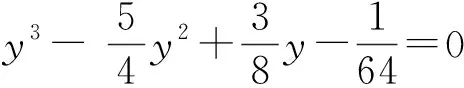
证明(a) 将结论1(a)的方程

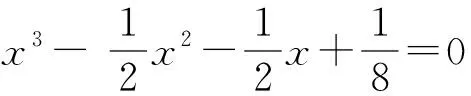
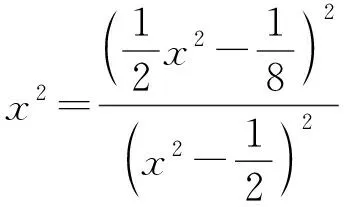
(4)

令x2=y，将式(4)变形为

并化简可得到

(5)

由结论1(a)知方程(5)的解为

(b) 对方程(5)，令y=1-u得

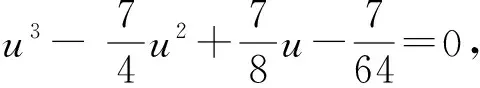
则由结论2(a)，结论2(b)得证.

3 应用

例1《数学通报》2015年10月号第2268号问题：试证明

证明根据一元三次方程3个根与系数的关系，由结论2(b)有

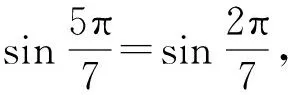
例2试证明

证明根据一元三次方程3个根与系数的关系，由结论1(b)即可得证.

显然，根据例2的3个等式，柳冉在文献[1]中所给的证明可以简单许多.关于正弦、余弦多倍角公式的应用，人们研究的更多的是2倍角和3倍角的情况，希望本文对余弦7倍角公式应用方面的研究能起到抛砖引玉的作用，期望有更多的数学爱好者对正弦、余弦多倍角公式的应用有更多的研究并产生更好、更漂亮的结论.