数学问题解答

2017年5月号问题解答

(解答由问题提供人给出)

2361若x,y,z是正实数，求证：

(1)

其中“∑”表示轮换对称和.

(四川成都金牛西林巷18号华鑫园A601 宿晓阳 610031)

证明设y2+z2=a,z2+x2=b,x2+y2=c.则a,b,c为三角形的三边.

于是(1)式等价于下列涉及三角形三边的不等式

(2)

由柯西不等式，有

(3)

又由b2≥b2-(c-a)2,知

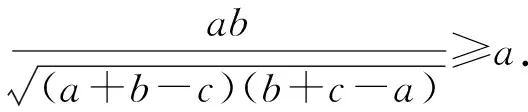
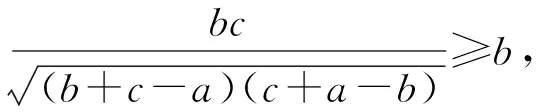
三式相加，得

(4)

(3)+2×(4)并开方，即得(2)式.故(1)式成立.

2362在△ABC中，a,b,c为其三边长，ra,rb,rc与ha,hb,hc是其对应三边上的旁切圆半径与高，则有

(hb+hc)(hc+ha)(ha+hb)

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

证明记△ABC的面积为S，注意到

应用正弦定理，以及三角恒等变形，得

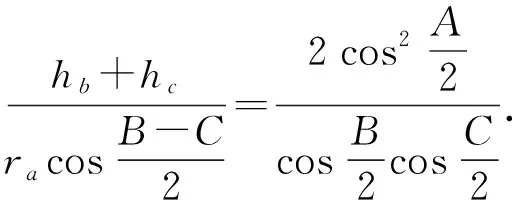
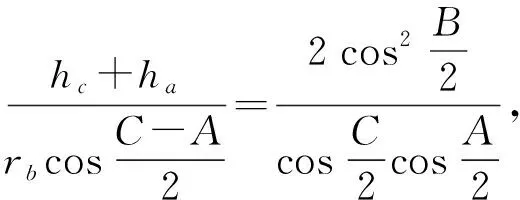
三式叠乘，立即获得

(hb+hc)(hc+ha)(ha+hb)

2363在△ABC中，AD、BE、CF相交于一点O，点D、E、F分别在△ABC三边BC、CA、AB上，则有

min(AD,BE,CF) ≤OD+OE+OF

≤max(AD,BE,CF).

(西安卫星测控中心 赵晓辉 714000)

证明不妨设AD≤BE≤CF，过O作直线MN平行于BC，交AB于M，交CA于N，则有

由此可得

即

OE+OF≥OA.

从而

OD+OE+OF≥OA+OD=AD.

类似可证

OE+OD≤OC,

得到

OD+OE+OF≤OC+OF=CF.

特别地，若AD=BE=CF，

则有OD+OE+OF=AD.

2364给定m≥3且m∈N，设a1,a2,…,am>0，n≥m且n∈N，求证：

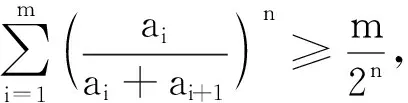
(湖南师大附中数学教研组 张湘君 410006)

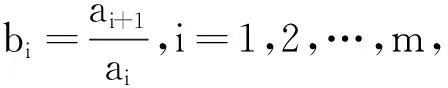
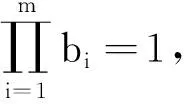
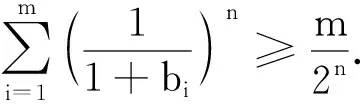
由幂平均不等式知

于是只需证明

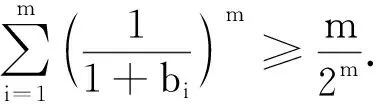
考虑到bi>0,i=1,2,…,m，

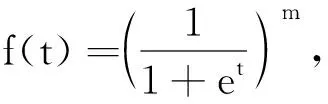
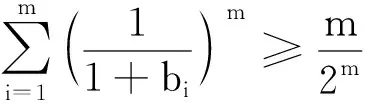
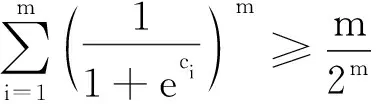
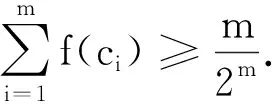
f″(t)=met(1+et)-m-2(met-1).

下面分两种情况讨论：

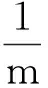
于是只需证明

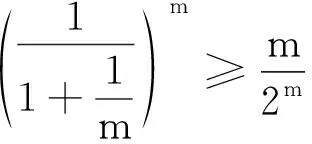
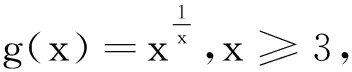
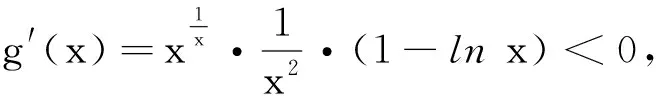
所以g(x)在x≥3时单调递减，

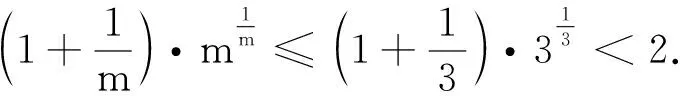
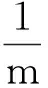
f″(t)≥0，则f(t)是下凸函数，

由琴生不等式得

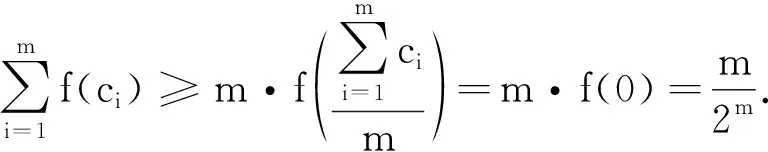
2365已知如图，在△ABC中，点P、Q分别在CB、BC的延长线上，AE垂直于∠ACQ的平分线于点E，BD1、BD2在∠ABP的内部，且∠ABD1=∠PBD2，AD1⊥BD1，AD2⊥BD2，直线D1E、D2E分别与直线PQ交于点H、G．

求证：△EGH为等腰三角形．

(北京市陈经纶中学 张留杰 100020)

证明如图，过点D1、D2作直线与PQ交于点F，

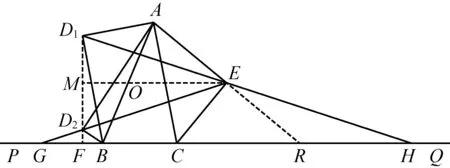
因为 ∠AD1B=∠AD2B=90°，

所以A、D1、D2、B四点共圆，

且这个圆是以AB为直径.

设圆心为O，则O为AB的中点，

所以 ∠BD2F=∠BAD1．

因为∠BAD1+∠ABD1=90°，

又∠ABD1=∠FBD2，

所以∠BD2F+∠FBD2=90°，

所以∠BFD2=90°，即D1D2⊥BC．

延长AE交PQ于R点，

因为CE平分∠ACQ，AE⊥EC，

所以易得△ACE≌△RCE，

所以AE=ER，即点E是AR的中点．

连结EO并延长交D1D2于M，

因为OE是△ABR的中位线，

所以EO∥PQ，所以EO⊥D1D2，

由圆中的垂径定理可得M是D1D2的中点，

所以易得Rt△EMD1≌Rt△EMD2，

所以∠D1EM=∠D2EM．

又∠D1EM=∠EHG，∠MED2=∠EGH，

所以∠EGH=∠EHG，

所以△EGH为等腰三角形．

2017年6月号问题

(来稿请注明出处——编者)

2366如图，G为△ABC的重心，D,E,F分别为边BC,CA,AB的中点，延长AD,BE,CF交△ABC的外接圆于点L,M,N，求证:

S△LMN≥S△ABC.

(山东省泰安市宁阳县第一中学 刘才华 271400)

2367设a,b,c为正实数，且abc=1，求证：

(安徽省岳西中学 储百六 246600)

2368如图，在△ABC中,点E，F，D分别在AC，AB，BC上且DE∥AB,DF∥AC,EN⊥AB,FL⊥AC,N、L分别为垂足，EN与FL交于H,求证：

AN2+AL2+BC2=BN2+CL2.

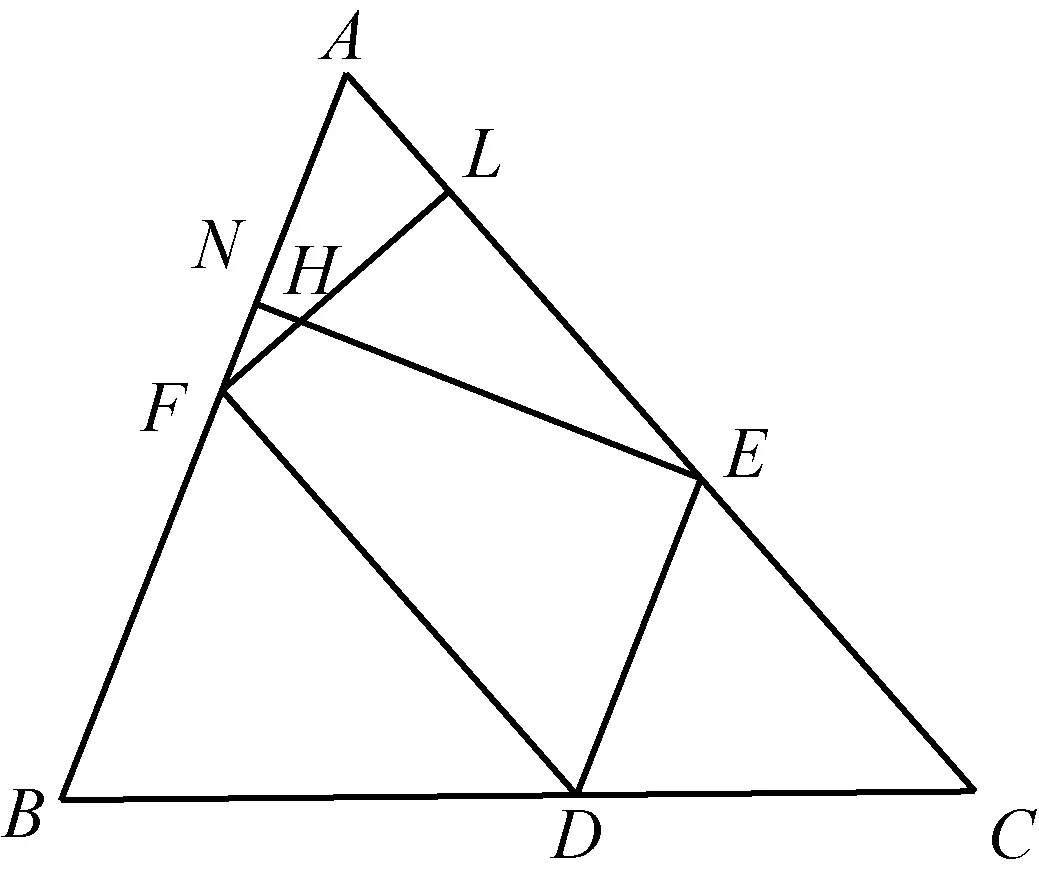
(江西师范高等专科学校 王建荣 335000，温州私立第一实验学校 刘沙西 325000)

2369设点I,H分别为锐角△ABC的内心和垂心,则有

(天津水运高级技工学校 黄兆麟 300456)

2370如图所示，从海岸上的P地瞭望某海岛周边的4座海洋科研观察站A，B，C，D，发现P，A，B与P，C，D分别处在同一视线上，又测得P地到海岛中心O地的距离为d千米，各观察站到O地的距离均为r千米.从P地到O地已建成直线通达的物流干线，现拟在海岛内的既有干线上设立中转站M，新建4条由M分别直线通达各观察站的物流支线，试确定中转站的选址，使得新建支线的总长度最短.

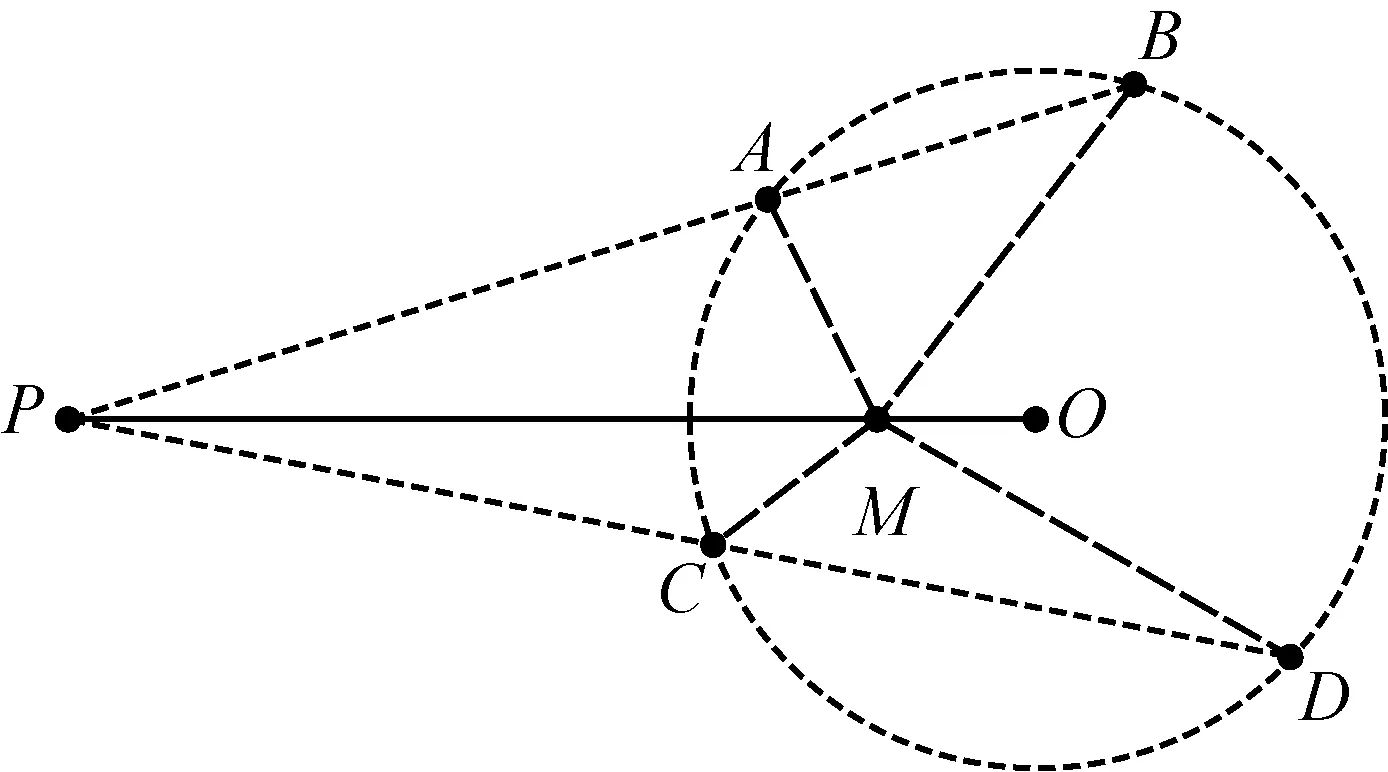
(河南省辉县市一中 贺基军 453600)