7～9年级学生概率认知中的“等可能性偏见”研究*

何声清 巩子坤

(1.北京师范大学教育学部 100875；2.杭州师范大学理学院 310036)

1 引言

概率素养(probabilityliteracy)[1]是当今社会公民必备的数学素养，概率内容也已然自上世纪末开始陆续进入各国的中小学数学课程标准(如美国[2]、英国[3]、我国[4]).然而诸多研究一再表明[5～7]，自学前到高中阶段，学生在概率认知及推理方面始终表现出不同程度的错误，“概率思维中的不当推理在不同年龄层之间广泛存在且十分顽固”[8].“等可能性偏见”是学生对概率概念的典型错误认知之一，并且已被国外诸多研究[9～14]一再证实.Lecoutre较早地对“等可能性偏见”进行了描述[11]，“在用一些外形对称的物体(如，硬币、骰子)进行随机试验时，人们认为各事件的结果总是等可能的.例如，同时掷2枚硬币，掷出‘一正一反’的概率理论上大于‘两个正面’.然而，许多人认为所有结果均是等可能的”.Amir的研究表明[15]，学生在概率决策时常常不当地用“50-50”对各事件的可能性一概而论.Tarr则进一步区分了学生在概率决策时不当使用“50-50”的两种典型表现[16]：一种误用是在预测两种以上等可能结果的随机试验中；另一种误用是在预测两种不等可能结果的随机试验中.

关于我国学生“等可能性偏见”的实证研究则相对较少.李俊首次对上海地区的6、8、12年级学生概率认知中的“等可能性偏见”进行了研究[17]，并将其具体区分为两种表现形式：一种认为随机试验所有结果的概率相等且均为50%，另一种认为所有结果的概率相等且均为1/n(n是指“学生能够列举的所有可能的结果总数”).高海燕对杭州地区6～12岁(1～6年级)学生的研究表明[18]，学生的“等可能性偏见”随年级递增不降反增.何声清等对杭州地区11～14岁(5～8年级)学生的研究表明[19]，学生在重复样本及包含组合运算的问题情境中更易于表现出“等可能性偏见”.然而纵观上述研究，以下问题尚待深究：承接高海燕的研究，我国中学生(7～9年级)“等可能性偏见”的表现如何？该偏见是如何随年级递增而发展的？两类“等可能性偏见”的表现有何差异？该偏见在不同概率任务中表现有何差异？该偏见在不同性别之间有何差异？本研究将对以上问题进行具体分析.

2 研究设计

2.1 测试工具

研究共设计了7个“摸球”任务(Tasks)，以考察学生对两个事件的概率进行比较的能力(表1).各任务按照“球的颜色种类”、“球的总数”及“盒子个数”等变量设置任务情境，其中任务1～2是“摸出1个球”的情境；任务3～7是“摸出2个球”的情境.

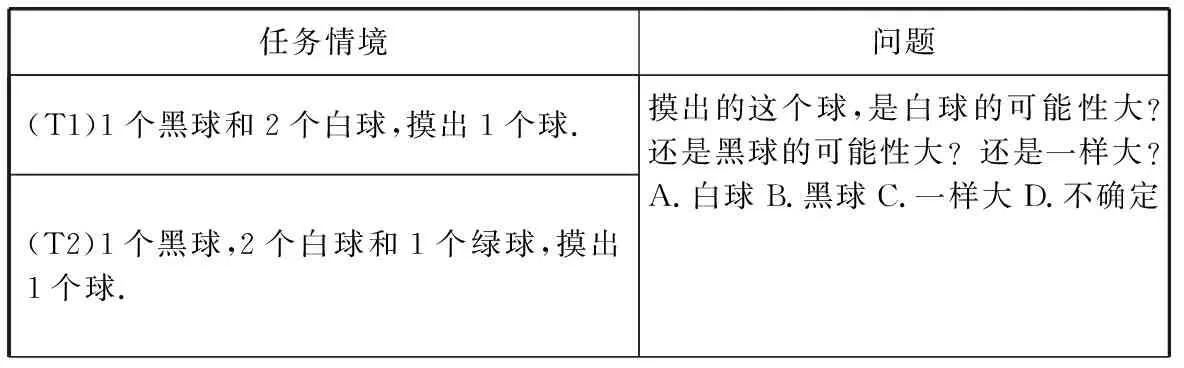
表1 “摸球”任务设计

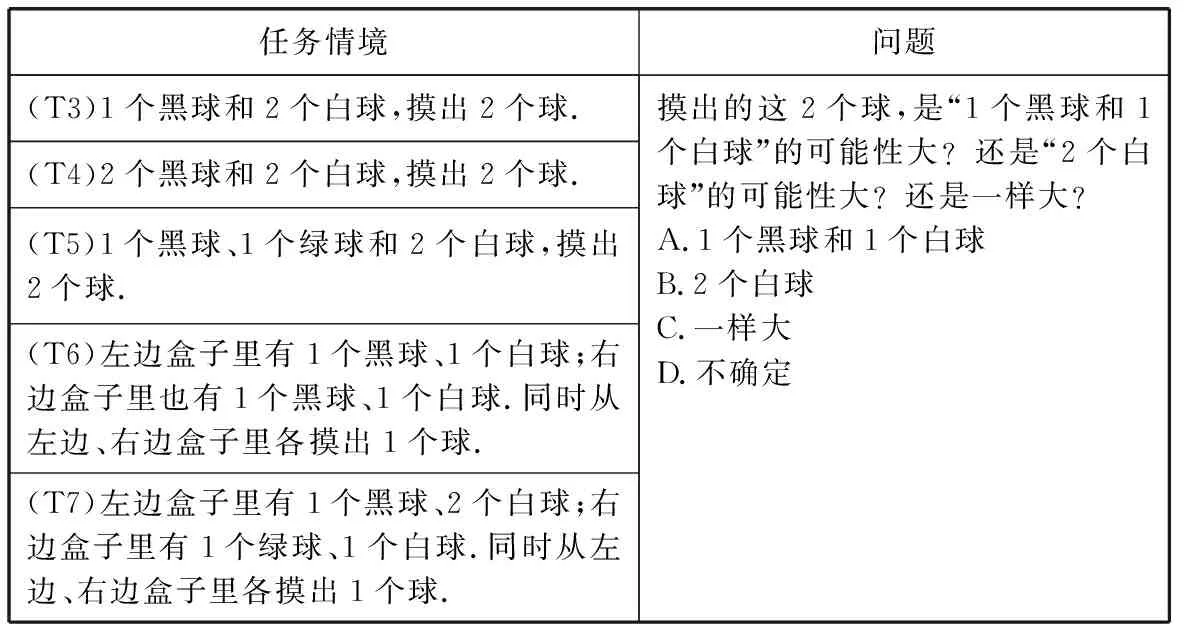
续表

(注：①各题目题干均是“一个(两个)不透明的盒子里(分别)有×个白球、×个黑球和(和×个绿球)，它们除颜色外都相同.闭上眼睛，摇一摇盒子后，从盒子里摸出2个球(各摸出1个球).”②除了要求对事件概率进行比较之外，各题均要求被试详细写出作答理由，用作判断学生问题解决策略的依据.)

2.2 被试

北京市某学校的204名7～9年级学生参与了本次测试，各年级的被试人数分别为69人、74人及61人，男、女生人数分别为113人和91人.

2.3 信度

对学生各题作答的内部一致性进行分析，结果表明，该测试卷具有较高的同质性信度(Cronbachα=0.771).

3 研究结果

在本研究中，李俊[19]提出的两类“等可能性偏见”再一次得到了证实.为了讨论方便，下文将前者称为第I类“等可能性偏见”(简称为第I类偏见)，后者称为第II类“等可能性偏见”(简称为第II类偏见).以T4为例，有被试认为“‘1个黑球和1个白球’与‘2个白球’的概率相等，因为两者的可能性均是50%”，这属于第I类偏见；有被试认为“有三种可能，所以三种可能各占1/3，因此‘1个黑球和1个白球’和‘2个白球’的可能性一样大，1/3=1/3”，这属于第II类偏见.

我们根据学生作答的情况以及提供的理由来分析他们是否持有两类偏见.

3.1 学生在“摸出1个球”任务中几乎没有表现出“等可能性偏见”

学生在“摸出1个球”任务中表现良好，总体正确率为93.87%，7～9年级学生的作答正确率分别为92.03%、91.22%及99.18%.在任务1和任务2中，分别仅有1.47%和1.96%的被试在其作答理由中表现出“等可能性偏见”，学生基本能够对判断做出合理解释.以任务1为例，有62.7%的被试认为“白球的数量(比例)多，所以摸出白球的可能性大”，有32.4%的被试更是列举了事件的样本空间(如，“摸出黑球有1种情况，摸出白球有2种情况”)，并据此认为“摸出白球的可能性大”.

3.2 学生在“摸出2个球”任务中明显表现出两类“等可能性偏见”，且两类偏见的发展趋势有所差异

学生在“摸出2个球”任务中的作答正确率则明显较低(40.1%)，7～9年级学生的作答正确率分别为28.41%、36.76%及57.38%.从学生的作答理由来看，学生在该类任务中则明显表现出较多的“等可能性偏见”(22.98%)，且各年级基本持平(分别为22.26%、24.36%及22.3%).学生的“等可能性偏见”没有随着年级的递增而明显消除，这也得到了已有研究[11]的支撑.将学生在该类任务上的作答正确率与“等可能性偏见”的百分比对比可推断，尽管学生在该类任务上的正确率随年级的递增有较明显的提高，但其持有的“等可能性偏见”却始终比较顽固.

纵向来看(表2)，7～9年级学生的第I类偏见随着年级递增有较明显的消除；而第II类偏见随着年级递增反而有较明显的增多.也就是说，尽管总体而言7～9年级学生“等可能性偏见”的百分比基本持平，然而若对两类偏见作具体分析，其发展趋势是不一样的，这是对已有研究[11]“‘等可能性偏见’在认知发展过程中长期存在”的进一步发展与完善.

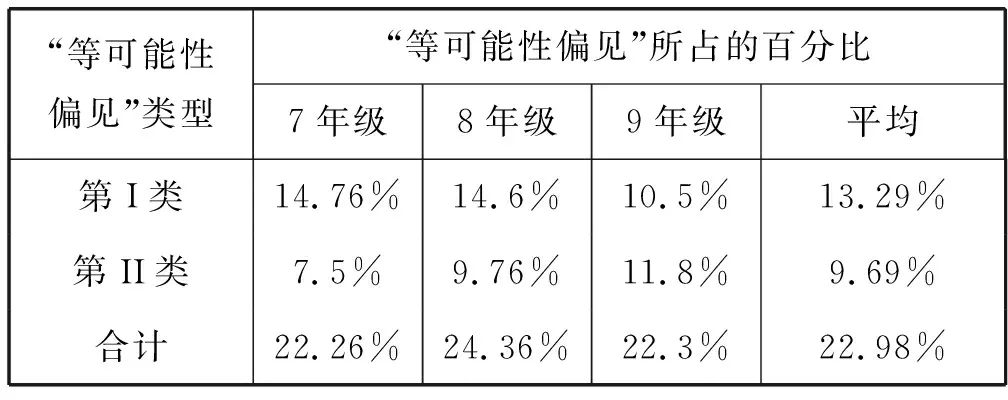
表2 学生在两类“等可能性偏见”表现上的差异

3.3 “等可能性偏见”是导致学生作出等可能判断的主要原因之一

对于“摸出2个球”任务，除任务7外，学生在各任务情境中的作答正确率均较低(表3).

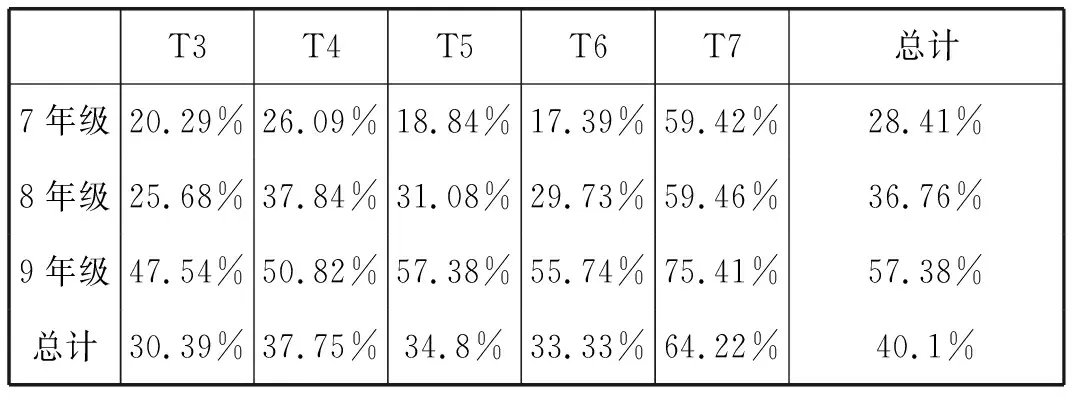
表3 学生在“摸出2个球”任务中的作答正确率

在该类任务中，T3～T6的答案均是“A.‘1个黑球和1个白球的可能性大’”，T7的答案是“B.‘2个白球’的可能性大”.然而在学生的作答中，选择“C.一样大”的百分比(42.35%)甚至超过了正确选项(40.1%).需要指出的是，选择“C.一样大”并不一定意味着学生一定持有“等可能性偏见”，其他方面的不良直觉或错误认识也是导致其做出此类判断的原因.例如，有的学生在T4中选择“C”的理由是“因为黑球和白球一样多，都是2个”或者“我猜的”.为此，我们进一步对学生的作答及其理由进行对比分析(图1)，结果发现，持有“等可能性偏见”的学生的百分比(22.98%)占了选择“C.一样大”的学生的百分比(42.35%)一半以上.具体到每一个任务，两者也均有类似的比例(T3，33.17% vs 49.51%；T4，26.46% vs 52.45%；T5，19.24% vs 34.31%；T6，24.8% vs 55.39%；T7，11.2% vs 20.1%).尽管没有对导致选择“C”的其他原因进行统计，我们基本可以说，持有“等可能性偏见”是导致学生选择“C.一样大”(等可能的判断)的主要原因之一.

图1 选择“C.一样大”与基于“等可能性偏见”的百分比对比

3.4 学生在不同任务情境中表现出的“等可能性偏见”有所差异

总体而言，各题中学生“等可能性偏见”的百分比从大到小依次是T3>T4>T6>T5>T7(表4).(1)学生在T3中“等可能性偏见”的百分比最高，且基本均是第I类偏见.(2)学生在T4和T6中“等可能性偏见”的百分比也比较高，这或许与题目的结构有关：该类任务中球的个数均是“2黑、2白”，T6中两个盒子里球的个数和颜色也均一致.学生常常把这种直观上的“对等”与结果的“等可能”建立不当的因果联系，“因为两种球都是2个，所以两个结果的可能性相等”.(3)学生在T7中“等可能性偏见”的百分比最低，这一方面可能是因为白球有3个，黑球仅有1个，直观上两者数量悬殊较大，这在一定程度上减少了学生对“两种情况等可能发生”的直觉判断，转而诉诸于其他的策略；另一方面，T7的问题情境是在“两个”盒子中“分别”摸球，这在一定程度上“分解”了摸球的动作，利于学生对摸出的球进行“组合”.换言之，学生可能在该任务上更多地诉诸于组合或其他策略.

需要指出的是，与T7相比，T6同样是从“两个”盒子里“分别”摸球的情境，但学生在该任务上“等可能性偏见”的百分比却相对较多.这是由于T6中黑、白球数量相等，且两个盒子外观对等，给“等可能性偏见”提供了直观的土壤.此外，与T6相比，T4中球的个数同样是2个黑球和2个白球，但学生在该任务上“等可能性偏见”的百分比却相对较多.一方面，这是由于T6是“分别”从两个盒子里“各”摸出1个球，如前文所述，这在一定程度上“分解”了摸球的动作，让使得对摸球结果进行“组合”成为了可能；另一方面，T6的样本空间(4种情况)小于T4(6种情况)，相对而言更容易列举出所有的可能结果，这在一定程度上给学生列举样本空间进而进行概率比较提供了便利，从而“等可能性偏见”这一不良直觉的百分比相较于T4更少.

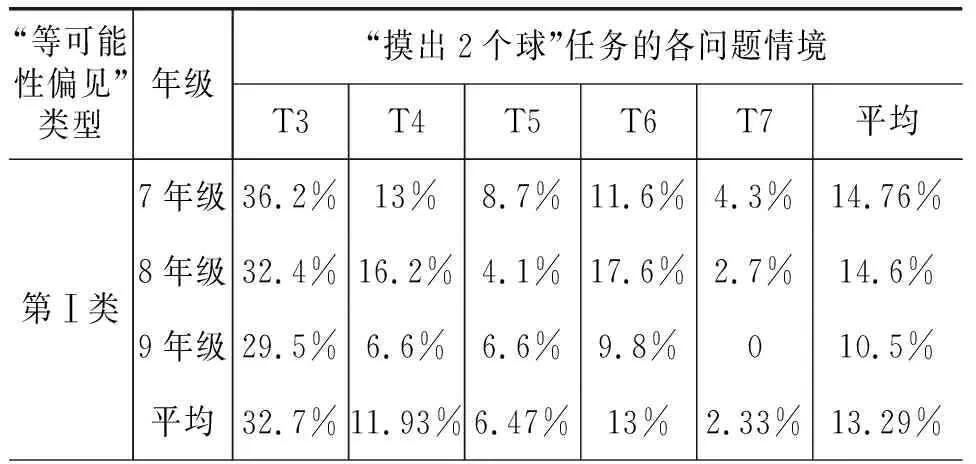
表4 学生在不同任务情境中表现出的“等可能性偏见”

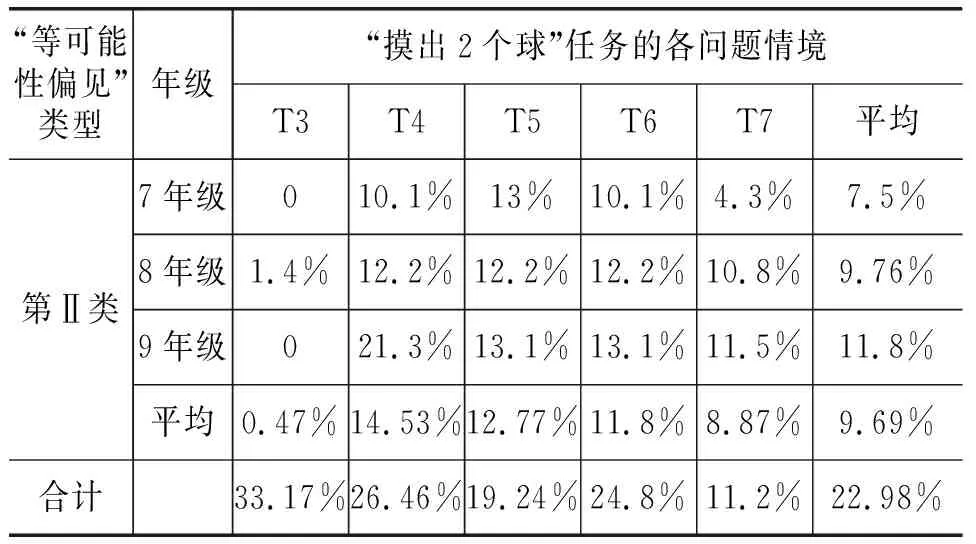
续表

3.5 学生“等可能性偏见”与直觉的发展有关

7～9年级学生两类偏见的发展是“此消彼长”的过程.从一般意义而言，第II类偏见相较于第I类有一定“进步”的方面：该类偏见不再将事件的概率作“二元”划分并采用“50-50”的思路进行解释，而是考虑到了试验结果的其他情况.也就是说，鉴于两类偏见的总体百分比在年级组间基本持平，那么第II类偏见百分比的提高(意味着第I类偏见百分比的降低)可以视为学生直觉上的“进步”.在T4中，9年级学生第II类偏见的百分比明显高于7、8年级，而第I类偏见则明显低于7、8年级；在T6中，9年级学生第II类偏见的百分比虽没有明显提高，但第I类偏见则明显降低.如前所述，T4和T6均是直观上“对等”的情境，这说明9年级学生在这类直观上“对等”的情境中能够摆脱简单的“二元”划分，其直觉有了一定的“进步”.在T5和T7中，各年级组间在两类偏见上的百分比变化不大，仅T7中第I类偏见有一定降低，以及8年级学生在第II类偏见的百分比有一定提高.这说明，在直观上“不对等”的情境中，学生虽然更多地表现为第II类偏见，然而其直觉并没有随着年级的递增有明显的“进步”.

3.6 男、女生的“等可能性偏见”无显著性差异

对男、女生在各任务上的得分进行差异分析.结果表明，男生(M=3.72，SD=1.8)和女生(M=4.09，SD=2.05)的得分无显著性差异(p=.17>.05).具体到每一个任务，男、女生也均无显著性差异(pT1=.992>.05，pT2=.943>.05，pT3=.107>.05，pT4=.443>.05，pT5=.119>.05，pT6=.094>.05，pT7=.899>.05).

对男、女生作答理由中表现出的“等可能性偏见”进行差异分析.结果表明，男生(M=1.09，SD=1.46)和女生(M=1.31，SD=1.81)无显著性差异(p=.35>.05).对男、女生在各任务上是否表现出“等可能性偏见”进行差异分析.结果表明，不同性别学生在各任务的作答理由中是否表现出“等可能性偏见”均无显著性差异(T1，χ2=.600，p=.439>.05；T2，χ2=.048，p=.827>.05；T3，χ2=.486，p=.486>.05；T4，χ2=1.560，p=.212>.05；T5，χ2=1.665，p=.197>.05；T6，χ2=1.118，p=.290>.05；T7，χ2=.601，p=.438>.05).

4 讨论与分析

4.1 本研究结果与国外研究的比较

在Green[20]的一项早期研究中，设计了一道在难度和结构[注]需要指出的是，Green的研究中D选项是“我不知道”，这与本研究中D选项“不确定”略有不同.上均类似于本研究T1的题目：班级里有13名男孩和16名女孩，老师将每位同学的名字分别写在一张纸条上并放进一顶帽子里.老师闭上眼睛从帽子里抽出一张纸条.请选择：A.男孩更容易被抽到；B.女孩更容易被抽到；C.男孩、女孩一样容易被抽到；D.我不知道.在接受测试的11～16岁学生中，有42%的被试选择了答案“C.男孩、女孩一样容易被抽到”.而在本研究中的T1中，仅有4名(1.96%)被试选择了“C.一样大”.在“更容易出现‘等可能性偏见’”的T3～T7中，我国7～9年级(13～15岁)学生才达到同等程度的百分比(42.35%).

以上仅从“学生作答”层面对两项研究进行了比较.如前所述，学生作出的等可能判断不完全源自于其直觉中的“等可能性偏见”.为此引用李俊的研究[17]对学生的“理由”进行更深入的比较.在李俊的研究中，在一项“理论上最容易出现‘等可能性偏见’”的题目中，11和13岁学生中共有28%的被试在作答理由中表现出了“等可能性偏见”.在本研究中，7～9年级(13～15岁)学生在“更容易表现出‘等可能性偏见’”的“摸出2个球”任务中，其“等可能性偏见”的百分比分别为22.26%、24.36%及22.3%，与李俊的研究基本一致.

承接高海燕[18]的研究，7～9年级学生的“等可能性偏见”总体上保持在同等水平，但两类具体的偏见则“此消彼长”.

4.2 造成“等可能性偏见”的原因分析

笔者结合已有研究及学生作答尝试对学生“等可能性偏见”的原因作出如下分析.

(1)构造样本空间时遇到困难

在以“摸球”模型为例的古典概型中，事件A的概率能够基于其包含的可能结果个数(m)及样本空间(n)而被进行理论计算(P=m/n).对于“摸出2个球”的任务，在构造样本空间时需要对各种可能的情况进行组合运算.以T4为例，其样本空间是“黑1黑2，黑1白1，黑1白2，黑2白1，黑2白2，白1白2”.因此摸出“1个黑球和1个白球”的概率为4/6，摸出“2个白球”的概率为1/6.然而，学生常常认为“共有3种可能的情况，即‘1个黑球和1个白球’‘2个白球’和‘2个黑球’，所以摸出‘1个黑球和1个白球’和‘2个白球’的概率均为1/3.”

(2)缺乏对概率“可度量性”的认识

对古典概型而言，事件的理论概率具有先验性.然而在作答中，学生常常会认为“至于哪种情况更容易被摸出，我们是无法预知的，因为事情还没有发生”，也正是这种错误观念导致学生在概率决策时走向“等可能性偏见”：“既然无法预知接下来会发生什么(或者说，既然各种结果都是有可能的)，那么我觉得各种情况的概率一样.”这也得到了其他研究的支撑.例如，在Savard[21]的一项有关“掷硬币”试验中，学生常常认为“硬币有两面，我们不知道落下时哪一面会朝上，因为硬币不是我掷的，所以各种可能性一样.”

(3)生活经验中的不良直觉

良好的直觉对于学生概率思维的发展有益无害[22]，然而不良直觉却对概率思维的发展造成干扰.研究表明[15]，学生生活经验中的朴素概率知识(informallyacquiredknowledge)和学校课程中呈现的概率知识(formalknowledge)常常具有潜在的冲突.在本研究的概率任务中，学生常常把题意中的“闭上眼睛摸球”和“等可能性”建立联系，其理由是“因为是闭上眼睛摸的(无法人为操控)，所以各种结果的可能性一样”.再例如，在所有的7个“摸球”任务中，“摇一摇盒子，摸出×个球”的本意是“随机摸出×个球”.然而有学生把“随机”曲解为“随意”，亦即“随我之意”，“我希望两种结果的可能性一样大，那么两者的可能性就一样大”.

(4) 不当的因果思维

确定性思维是一种“关系思维”，它依据当前或过去的信息对现象进行解释，因果关系在其中扮演着重要角色.如前文提及，对于T4和T6这类直观上“对等”的情境，学生常常把这种直观上的“对等”和结果的“等可能性”形象地建立了因果联系.在以往的一项研究[19]中，我们组织学生进行有放回地摸球试验，让其摸10次并记录结果.统计结果显示，10次摸球中有5次摸出的是白球，另5次摸出的是黑球.学生在试验之后常常断定“如果再摸出一个球，两种颜色球的可能性一样大，因为前面10次中二者机会均等.”显然，学生把“前10次的试验结果”和“理论上的概率”建立了不当的因果联系.

5 结语

学生在“摸出1个球”任务中几乎没有表现出“等可能性偏见”；在“摸出2个球”任务中表现出的“等可能性偏见”学生百分比为22.98%，并且没有随着年级的递增有明显的减少.尽管随着年级的递增，第I类“等可能性偏见”的“消”和第II类“等可能性偏见”的“长”可以认为是学生在直觉上的一种“进步”，但这类偏见始终没有企及概率决策的本质.为此，教师要认识到教学该类概率问题的困难性与艰巨性，与此同时，积极引导学生认识概率的“可度量性”，并逐步引导学生构造样本空间对其进行理论计算.此外，教学应帮助学生摆脱生活经验中不良直觉的影响，有意识地发展学生的概率思维.