倒过来思考 让思维更流畅*
——学习《做数学是倒过来的》一文有感
崔志荣
(江苏省东台市安丰中学 224221)
1 精彩再现
近日,在网上学习了一篇文章《做数学是倒过来的》,该文是中国科学院院士林群在2009年“翱翔计划”启动会上的科学家报告,文章着重讲述了,数学的思维与用处.读罢此文,感触颇深,尤其是林院士介绍的“笛卡尔发现四面体重心的思维过程”,特别有意思,以下与读者再来回味这精彩的思维过程.
大家思考一下这个问题:任意一个四面体的重心在哪儿?笛卡尔说,这个问题太难了,谁能猜出来重心在哪里?笛卡尔的想法是,虽然搞不清楚“任意四面体的重心在哪里”,但可以想象将它的一个顶点压低一点,再压低一点,一直压到底面内,四面体就变成了三角形.如果任意四面体的重心不会求,把它压成一个三角形,三角形的重心会求吧?笛卡尔是个很“笨”的人,他说,这个我也不会,三角形是各种各样的,有大有小、有胖有瘦,不同形状的三角形重心会在什么地方呢?这个问题,笛卡尔也不会.但是他想,把三角形的一个顶点往下压,直到把这个顶点压进另一条边内,这样一个三角形就变成了一条线段,笛卡尔又问:一条线段的重心在哪儿?是在中点上.所以你看,笛卡尔他很“笨”,看到一个问题他不懂,就会追根到底,一定要搞个水落石出.当他把任意一个四面体变成一条线段的时候,他说,这个问题我会了,线段的重心是在中点上,用他的话说,这是一个挑扁担的农夫都知道的.如果这个会了,我就知道任意三角形的重心在哪儿了,一个三角形可以认为是由一根一根长短不一的火柴棍摆起来的,每一根火柴棍就是一条线段,由于每根火柴棍的重心都在它的中点上,所以整堆火柴棍组成的三角形的重心就在三角形的中线上,因此笛卡尔就说,一个三角形的重心一定在一条中线上.这个大家同意吧?你看,笛卡尔多“笨”啊,只有这样讲他才懂.然后,他分别以三角形的三条边为底摆火柴棍,就有由火柴棍的重心组成的三条中线,由于三角形的重心是唯一的,因此三条中线必须交于一点.于是,笛卡尔就把这么一个复杂的问题,一下子变成了“一条线段的重心何在”、“一个三角形的重心何在”的简单问题了,事实上,这就已经从直观上发明了“三角形的三条中线交于一点”的定理.
这样的证明,我们一辈子都不会忘记.但如果从平面几何公理出发证明,你们刚刚学过能记住,等你们大学毕业,保证就忘光了.笛卡尔的发明方法使你一辈子都能记住,因为你不靠死记硬背,笛卡尔不仅告诉你定义、定理的证明方法,还会告诉你发明的方法.从他的发明,就知道三角形三条中线一定交于一点,这个点就是三角形的重心,而四面体可以被看作是以四面体的一个面为底,由一个一个的三角形向上堆起来的,每个三角形的重心连成了一条线,而分别以四面体的四个面为底面堆三角形,就有四条由重心连成的线,这四条线交在一点上,这个点就是四面体的重心.你看这个问题多简单!原本多复杂的一个问题一下变成了一个多简单的问题了,把一个科学家只有绞尽脑汁才能想出来的问题,变成了一个农夫就能解决的问题了.
以上笛卡尔这种倒过来做数学的方法,实际上就是特殊化思维,四面体的极限情况是三角形,三角形的极限情况是线段,然后,通过线段的重心反思三角形的重心,再由三角形的重心反思四面体的重心.这正如我国著名数学家华罗庚教授所讲,善于“退”,足够地“退”,“退”到最原始而又不失去重要性的地方,是学好数学的一个决窍.
2 问题反思
数学大师们的这种倒过来做数学,退到最简单情形思考的思维方式,对我们中学数学的教与学,应有深刻的指导意义!然而,笔者在思考,我们中学教师有没有用心去启迪学生的这种特殊化思维方式呢?我们的学生是否善于运用这种思维方式去解决数学问题呢?值得疑问.比如,两角差的余弦cos(α-β)公式的教学,我们有没有真正引导学生倒过来做数学,让学生自主发现公式呢?也许有教师说,该公式的生成,我们充分引导学生思考,以学生探究为主,而后生成公式.那好,如果在高考中,出这样一道题:谈谈两角差的余弦cos(α-β)公式的发现过程,并证明.高考后,会不会骂声一片呢?2011年陕西高考数学试题:叙述并证明余弦定理.还没有要求考生研究公式的发现过程,就被骂得不轻.
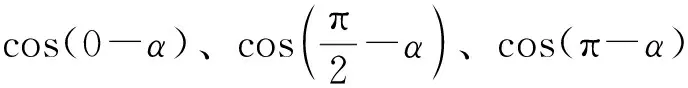
另外,纵观两角差的余弦cos(α-β)公式的新授课,读者有没有注意到,绝大多数课是20~25分钟完成公式的生成,然后是公式的运用.很显然,学生自主探究,不可能这么快发现公式,他们都比那些数学先辈们聪明?其实是我们教师过度引导所致,是学生已经预习过公式,假探究而已,没有充分让学生倒过来做数学.文[2]作者提出,不预习的课堂也很精彩,笔者非常认同,让学生进行本真探究,真正还原公式的发现过程,恐怕学生一节课也未必探究得出来!让学生课后继续思考,并把探究过程以及证明方法整理成数学小论文,第二节课再继续交流,那才能算接近真实的探究!
3 案例分析
上文说明,退到最简单情形,倒过来做数学,学生(包括我们教师)其实悟得并不深.类似的一些其他倒过来做数学的方法,我们也同样有问题,以下笔者试举一些案例,以此说明要加强倒过来做数学的解题意识,并需要切实用到教学中去.
3.1 分析法
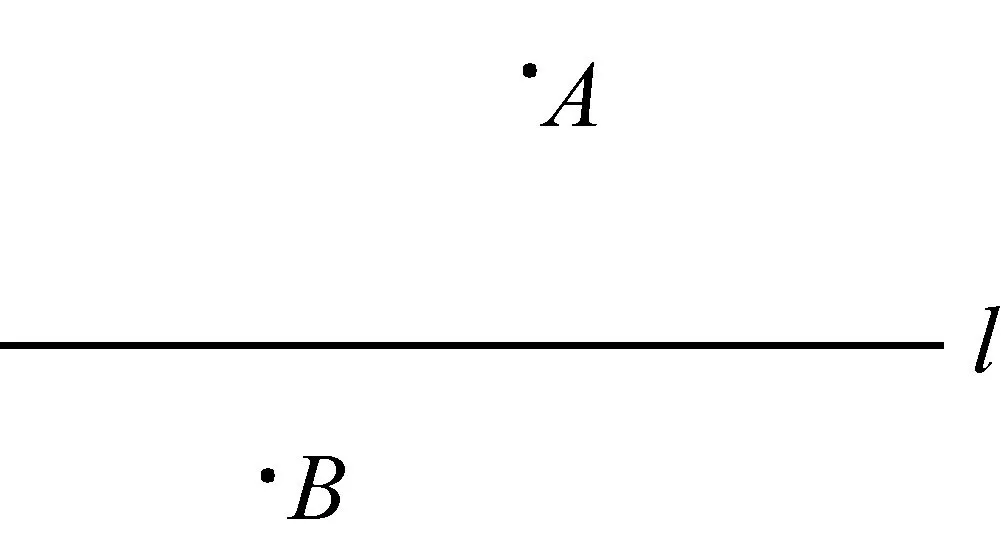
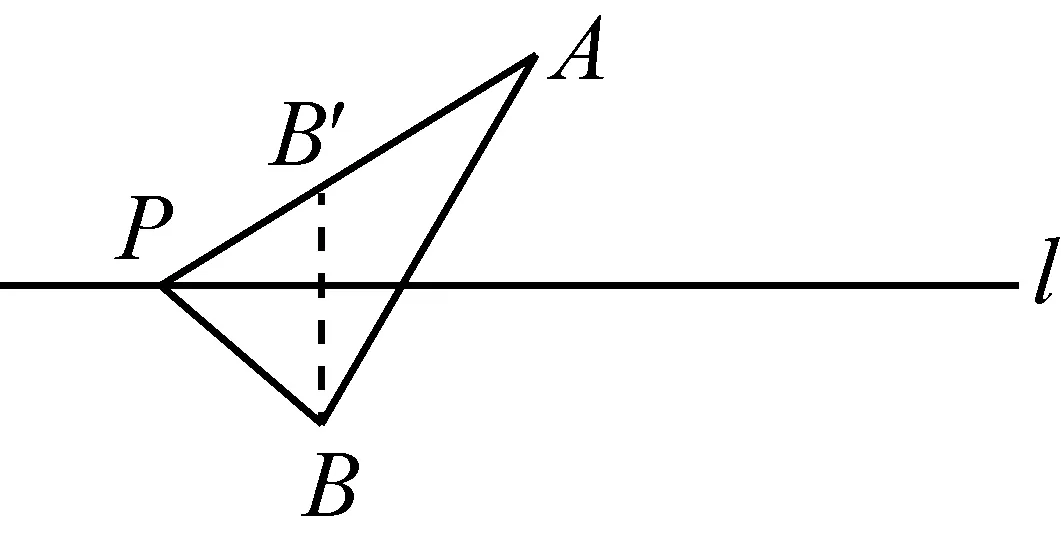
案例1已知点A(x1,y1),B(x2,y2)(x1 案例2若方程lgx=3-x的解x0∈(k,k+1),k∈N+,则运用二分法可得x0所属的下一个区间为__________ 易分析,方程对应的函数f(x)=lgx+x-3单调递增,又计算得f(2)<0,f(3)>0,所以x0∈(2,3),运用二分法,应计算f(2.5)=lg2.5-0.5的正负,怎样判断其正负呢?很多学生想到的是计算器,却很少有学生倒过来想,要得f(2.5)的正负,即比较lg2.5与0.5,即比较2.5与100.5,即比较2.52与10,即比较6.25与10,很容易得到lg2.5<0.5.这种倒过来的比较方法,其实就是分析法的思路,此例再次说明,用分析法倒过来做数学,中学师生的意识还是比较薄弱的! 有些证明题,难以由条件直接推理证明出结论,可以反设结论,由此推理出与条件、定义、定理等矛盾,这种证明方法叫做反证法.反证法也是一种倒过来做数学的典型方法,一些否定性结论,结论是“至多”、“至少”类的问题,常用反证法.还有一些不等式的证明,也可以用反证法,反设结论的不等方向找矛盾.其实,也有一些非证明问题,也需要采用反证法的思路,倒过来做数学,思维才得以顺畅. 案例4已知A,B,C三人中,有一人是真理,他总说真话;有一人是谎言,他总说假话;还有一人是智慧,他的话真假难辨.以下是他们表明自己身份的话,你能判断A,B,C的身份吗? A说:B是真理;B说:我是智慧;C说:B是谎言. 推理判断问题,其实也需用反证法的思路,先确定一个结论进行推理,有矛盾再转换结论,直至所假设结论与条件都相容为止.这也是倒过来做数学,直接由条件难以推理出结论,先假设一个结论,再推理,就思维畅通了.案例3,若假设A是真理,而真理总说真话,所以B是真理,矛盾;若假设B是真理,但他又说“我是智慧”,也矛盾;所以C是一定真理,那他说的一定是真话,所以B是谎言,所以剩下的A就是智慧了. 案例5如图1,在同一平面内,点A,B是直线l异侧的两点,试用尺规作图在直线l作出点P,使得直线l平分∠APB. 图1 图2 案例5是笔者上初二的女儿问的一道题,说句老实话,教高中数学,长期不接触尺规作图,受经验所制约,还就不能立即看出作图方法,怎么办呢?我们可以运用倒过来做数学的思路,假设已经作出点P(如图2),连接AP,BP,这时思维就自然流畅了,我们可充分运用角平分线的相关知识,如角平分线的性质定理、等腰三角形的三线合一、利用角平分线构造全等三角形等等,试图发现图形的一些性质,由此笔者发现了,过点B作直线l的垂线交AP于点B′,由三角形全等可知,直线l垂直平分线段BB′.如此思考,笔者最终找到了尺规作图的方法:过点B作直线l的对称点B′,连AB′交直线l与点P,点P即为所求.笔者把自己的思路分析给女儿听后,她说,爸爸还有点聪明哎!其实,不是聪明不聪明的问题,是数学思想方法的运用,是分析出来的! 通过对林群院士这篇文章的学习、反思、以及一些案例的分析,结合中学数学教学,笔者有两点想法,与读者交流. (1)启迪思维是数学教学的重要任务.我们常听很多人抱怨,学习数学有什么用呢?包括笔者以前也曾质疑过,社会很多职业并不需要太多数学知识,我们为什么要所有中小学生都学习数学呢?让少数数学优秀的学生学习数学,为一些高尖端的科学技术服务,不就行吗?笔者当时的认识错了,把数学教学仅局限于数学知识的传授.其实,数学教学的任务是多方面的,需要学生掌握数学思想方法、需要启迪学生的思维,引导学生学会思考问题等等.文[3]作者谈到,数学素养包括:数学思考与推理等.确实如此,像林群所讲的“倒过来做数学”,就是一种思维方式,学生需要学习并掌握这种逆向思维,在他们将来的社会活动中思考问题,大有裨益!比如,从事刑侦的警察,就要有很强的推理能力,他们需要根据案发现场、受害者的陈述等,寻找破案线索,这种抓住结论(案发现场)的逆向推理,就有点类似于我们倒过来做数学.我们生活社会上,会遇到不少问题需要解决,当然离不开思考,学生时代学习的数学思维方式,自然会有潜移默化的影响. (2)重视数学思维的感悟教学.本文所讲的倒过来做数学,只涉及一些重要的思想方法,如特殊化、分析法、反证法等.也许有读者会认为,这些方法都很常规,学生不难掌握,有必要大张旗鼓地谈论这个问题吗?上文问题反思中,谈到cos(α-β)的展开式.有多少教师能保证,你所教过的学生能顺利说出公式的发现思路及具体的发现过程呢?上文案例1,只有一名学生想到分析法,不能不说明,我们这方面的教学还或多或少存在一些问题.现行教材专门有一章内容《推理与证明》,研究本文所涉及到的方法,当时的新授课是不是快了,学生理解并不深刻?除了这章内容,我们解决问题的视角是不是窄了,这类方法用得少了?即使用到这些方法,我们是不是引导过度,学生缺少思考感悟、缺少过程处理的体验呢? 其实,我们不能把这章内容作为知识学习,而应该教会学生思考,运用这些重要的思想方法去解决问题,不能仅仅限于这一章内容的教学,而应该渗透到整个高中数学教学中去(包含这章内容之前,比如分析法,教材上基本不等式的证明,就已经运用了),让学生充分思考这些方法的运用,让学生充分感悟这些思维方式! 此外,作为数学教师,我们要提升专业素养,加强对数学的理解和认识,不能只教课本上的死知识,而要关注知识的生成与理解;不能就题解题,而要多与学生探讨问题的本质;不能仅是题型与方法的简单归纳,而要多启迪学生思维,引导学生多视角思考问题、多角度思考方法.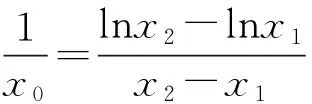
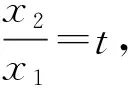
3.2 反证法
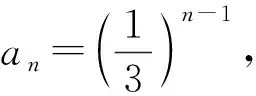
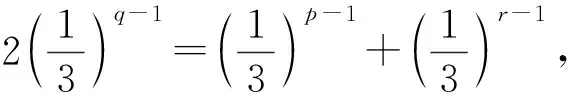
3.3 尺规作图
4 学习感悟

