关于两道数学奥林匹克题的推广与证明

喻德生

(南昌航空大学数学与信息科学学院 330063)

1985年第26届国际数学奥林匹克竞赛一道候选题是这样的[1]：已知:三角形ABC及形外的点X,Y,Z,∠BAZ=∠CAY,∠CBX=∠ABZ,∠ACY=∠BCX，求证：AX,BY,CZ共点.该题的证明，通常要利用正弦定理和梅内劳斯定理的逆定理，较具技巧性.本文利用有向度量定值法[2-7]研究该问题，得到一个涵盖面十分广泛的定值定理.利用该定理，不仅容易推出该题和另一道数学奥林匹克题的结论，而且还将它们推广到更为广泛的情形.

定义1[2]三角形P1P2P3各边PiPi+1(i=1,2,3;P3+j=Pj，以下类同)所在直线把平面分成两部分，三角形所在的部分称为直线PiPi+1的内侧，另一部分称为直线PiPi+1的外侧.

定义2[2]设点P0(x0,y0)到直线l:Ax+By+C=0的距离为dP0-l，则称该点到该直线带符号的距离±dP0-l为点P0到直线l的有向距离，记为DP0-l.即DP0-l=±dP0-l，其中当Ax0+By0+C>0时，取“+”号；当Ax0+By0+C<0时，取“-”号.

特别地，当dP0-l=0，即P0在直线l上时，规定P0到直线l有向距离为零，即DP0-l=0.

显然，点到直线的有向距离具有有向性：点P0到方向相反的两直线l:Ax+By+C=0与l-:-Ax-By-C=0有向距离的绝对值相等，符号相反，即DP0-l-=-DP0-l.

根据定义2和点到直线距离公式，容易证明点到直线有向距离公式：

引理1[2]点P0(x0,y0)到直线l:Ax+By+C=0的有向距离

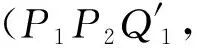
(1)

(2)

证明(i)如图1所示.设三角形P1P2P3顶点的坐标为Pi(xi,yi)(i=1,2,3)，可得PiPi+1外侧三角形PiPi+1Qi顶点Qi的坐标为[2]

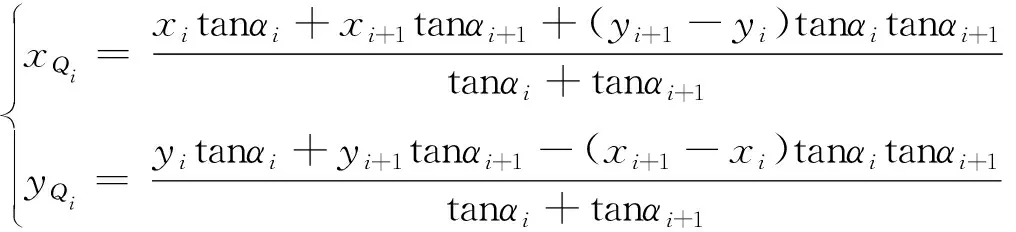
设任意点的坐标为P(x,y)，于是由有向直线PiQi+1的直线方程

(yi-yQi+1)x+(xQi+1-xi)y+(xiyQi+1-xQi+1yi)=0

图1

和点到直线的有向距离公式，可得

dPiQi+1DP-PiQi+1=(yi-yQi+1)x+(xQi+1-xi)y+(xiyQi+1-xQi+1yi).

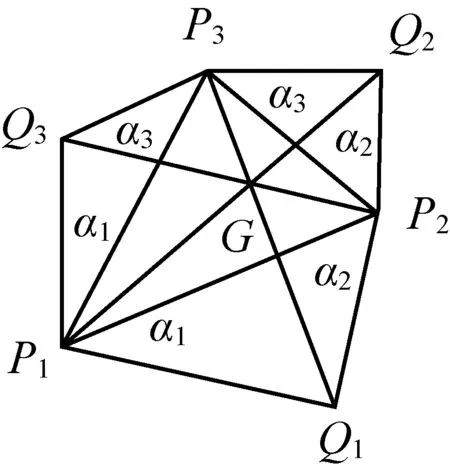
图2

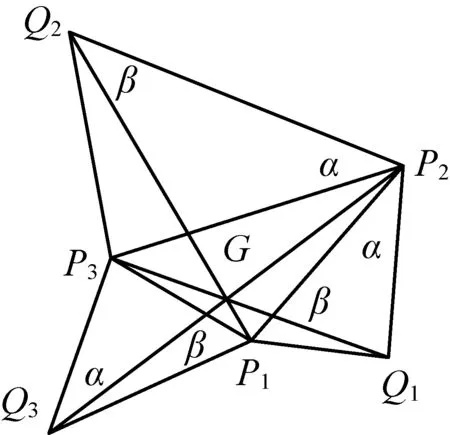
图3

因为

(yi+1tanαi+1+yi+2tanαi+2)]

类似地，可得

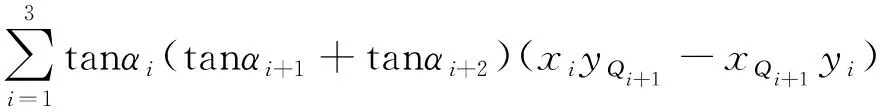
tanαitanαi+1tanαi+2

(yi+1yi-yiyi+1)]

=0，

所以

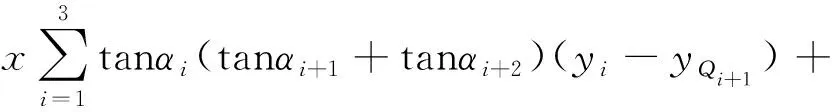
=0，

因此式(1)成立.

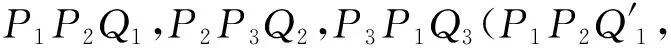
证明(i)如图2所示.设P1Q2,P2Q3所在直线的交点为G，则DG-P1Q2=DG-P2Q3=0.代入式(1)并注意到tanαi(tanαi+1+tanαi+2)dPiQi+1≠0，可得DG-P3Q1=0，因此G在直线P3Q1上.故P1Q2,P2Q3,P3Q1所在直线相交于点G.

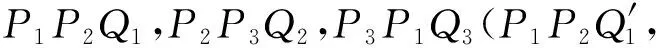
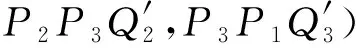
证明如图3所示.设∠P2P1Q1=∠P3P1Q3

注三角形各边外侧三角形的情形，推论1即为1985年第26届国际数学奥林匹克竞赛候选题；而当P1P2P3锐角三角形时，推论2即1973年第7届全苏数学奥林匹克题的第(2)部分.但应注意本文定理及其推论，对αi∈(0,π/2)∪(π/2,π)(i=1,2,3)都成立，因此即使是对三角形各边外侧三角形的情形，两推论的范围比两竞赛题的结论也要广泛得多.这种非常一般性的结论，用传统方法是不易证明的.