初三几道模拟试题的命制与思考

●

(无锡外国语学校，江苏 无锡 214031)

初三几道模拟试题的命制与思考

●张涛

(无锡外国语学校，江苏 无锡 214031)

文章以初三几道模拟试题的命制过程为例，浅谈试题的命制历程和思考感悟，以期引发同行加强命题的研究，精选符合课标要求的试题，深层改编有价值的题目，注重命题的导向，反复打磨试题.

模拟试题；命题过程；命题感悟

《2017年江苏省无锡市初中数学中考指导意见》明确指出：数学学科中考，具有初中毕业合格考试和高级中等学校选拔性考试两重性质，既是对学生在初中阶段所学数学知识和数学方法的全面考查，又为高级中等学校选拔录取新生提供依据.因此，考试既要有基础性，又要有一定的区分度.而一模考试又是中考复习阶段的第一次模拟演练，具有仿真性、诊断性、导向性等特点，因此命题者必须思考如何遵循课标、紧扣教材、贴近中考、合理控制难度，保证区分度和信度，并进行适当创新.笔者结合近期几道模拟试题的命制经历，谈谈试题的命制过程和感悟思考.

1 试题选编

选题一般来源于教材、教辅、模拟题、中考题，要求题目符合考试范围和课程标准.为了体现考试的公平性原则，部分试题还需要改编或原创.

1.1 精选原题

例1若一个多边形的内角和是1 080°，则这个多边形的边数为

( )

A.6 B.7 C.8 D.10

说明此题来源于课本习题，考查多边形的内角和公式，属于容易题.选择此题主要有两个目的：一是检测学生基础知识是否过关，引导师生重视教材，重视四基；二是激励学生，增强学生的信心，克服对考试的恐惧心理.

例2二次函数y=-(x-1)2+5，当m≤x≤n且mn<0时，y的最小值是2m,最大值是2n,则m+n的值为

( )

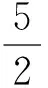
说明此题是2016年浙江省舟山市的数学中考题，主要考查二次函数的最值问题、二次函数的增减性和分类讨论的思想，考查基础知识、思想方法和能力素质，对学生能力要求较高.从阅卷情况来看，本题起到了很好的区分效果.

1.2 推陈出新

( )

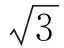
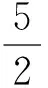
说明本题是由一道中考模拟题(例4)改编而来，原题内涵丰富，解法多样，是一个经典问题.

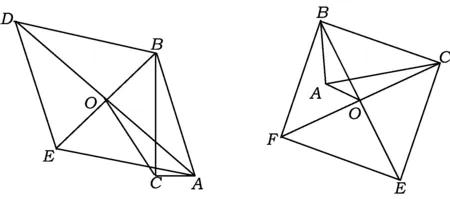
图1 图2

(2013年黑龙江省哈尔滨市松北区二模数学试题第20题)

深入探究，笔者发现，例4可进行一般化推广和多种变式，如：

笔者选取了变式2为背景，在适当赋值和调整图形后，得到了例5，考虑到此题的难度，将它作为选择题的压轴题.

例5如图3，矩形OABC的3个顶点O(0,0)，A(0,5)，C(7,0),P是边AB上的一个动点，将△OAP沿着OP翻折到△OA′P.

2)若点A′恰好落在∠BCO的角平分线上，求点P的坐标；

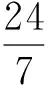
说明本题的问题背景取自例6.

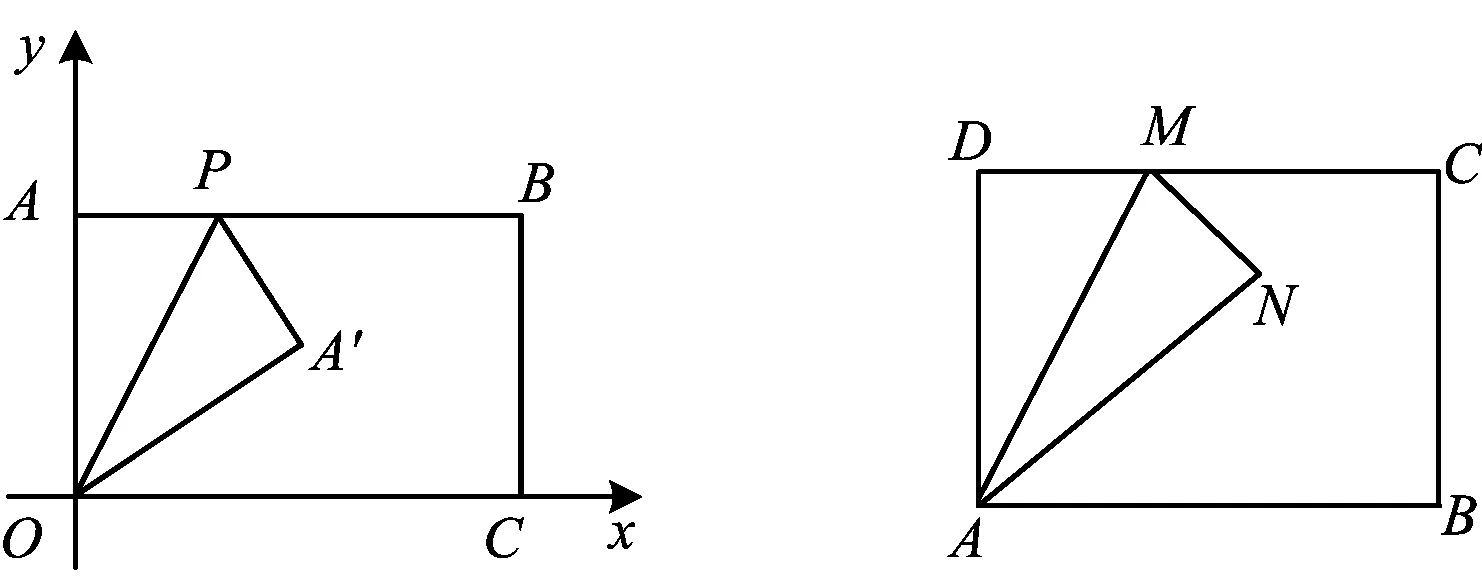
图3 图4

例6如图4，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．

1)当AN平分∠MAB时，求DM的长；

2)联结BN，当DM=1时，求△ABN的面积；

3)当射线BN交线段CD于点F时，求DF的最大值．

(2016年福建省福州市数学中考试题第26题)

原题在平面几何的背景下，让图形动起来，前2个小题属于“特殊性”的考查，第3)小题则是对“一般性”的考查，3个小题设问简洁，层层递进.笔者对原题的改编经历了如下的思考：

第2)小题，仍从一个特定情况进行考查，初步选择了如下7个位置：如图3，①点A′恰好落在边OB上；②点A′恰好落在边AC上；③点A′恰好落在边PC上；④点A′恰好落在边AB的垂直平分线上；⑤点A′恰好落在BC的垂直平分线上；⑥点A′恰好落在∠B的角平分线上；⑦点A′恰好落在∠BCO的角平分线.任选以上一个作背景，都能考查学生利用相似三角形、勾股定理解决问题的能力，最终笔者选择⑦作为条件，旨在启发学生思考出现两个解的原因，探究点A′的轨迹是以O为圆心、OA为半径的圆弧，∠BCO的角平分线与圆弧有两个交点，为解决第3)小题作铺垫.本质上，第1)和第2)小题都是考查边AP长度的求法，为了体现设问的多样性，问题分别以“求△OAP的面积”“求点P的坐标”的形式呈现.

第3)小题，与原题风格保持一致，考查最值问题，学生可以从点A′的轨迹出发进行解答.原题考查相切的特殊位置，笔者则从“垂线段最短”的角度考查最小值问题，将图形架构到坐标系中，从而给出直线的解析式.

1.3 打磨原创

说明为了保证试卷的区分度与信度，笔者打算编制一道压轴的填空题.首先，笔者确定了题目基调：以函数为背景，有特殊角，能考查方程、函数、数形结合等思想，考查学生基本数学素养.于是，试题的原始方案应运而生.

初稿A,B是y=-2x+4图像上的两个点，A(1，2)，O为原点，若∠AOB=45°，则点B的坐标是______.

从命题意图上看，初稿基本可取.初稿的答案有两个，需要讨论点B在点A的上方、点B在点A的下方两种情况.由于两种情况中点B坐标的求法完全相同，本题的考查重点并不是分类讨论，且全卷中已有两处考查到分类讨论的思想，因此又将题目进行了两次改编，得到例7.定稿中角度改为135°，增加了对学生转化能力的考查.在试做过程中，发现从不同角度切入都可以解决问题.比如：

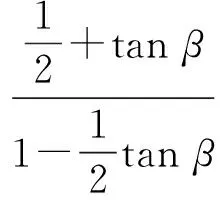
从而

设B′(3m,m),则

解得

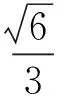
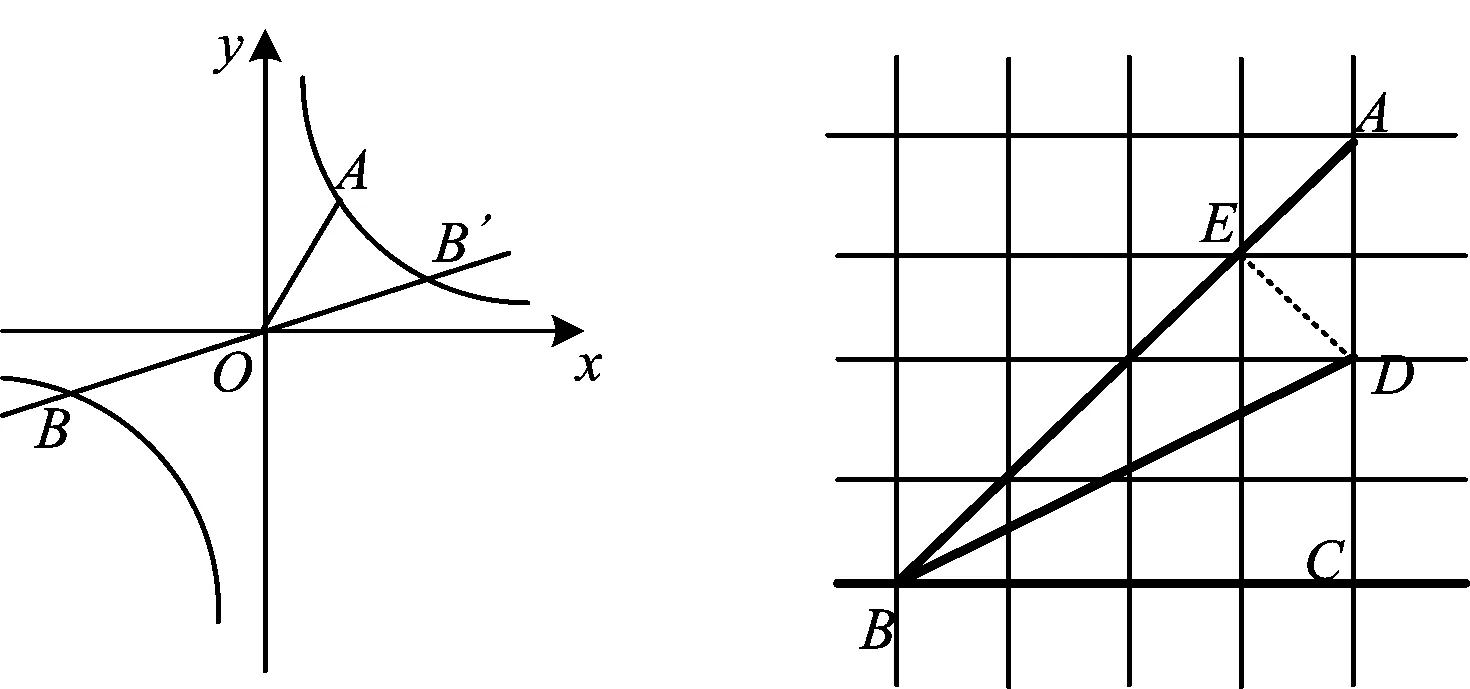
图5 图6

当然，这里也可以通过格点图来求tanβ(如图6所示).

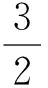
解得

图7 图8

解得

事实上，此题还可以通过构造一线三等角、母子型相似等方法求解，限于篇幅，不再赘述.需要指出的是，不同的解题思路，不同的切入角度，体现了不同的思维层次，带来了不同的解法，有繁有简.因此，该题在一定程度上也是对不同思维分析推断方法的考查[1].可以说，本题入口较宽，方法多样，有一定的探索性，基本达到了命题意图和考查目标.当然，笔者还希望通过本题传递这样的教学导向：在教学过程中，要多给学生探究的时间和空间，让学生经历数学知识的发现、形成过程，参与到寻求解题思路、优化解题方法的过程，并引导学生感悟数学思想、积累解题经验，注重培养学生的发散思维和创新意识.

例8三月春盛，十里桃花，白真与折颜围棋对弈，假如白真、折颜每局比赛输赢的机会相同，且白真已经赢得了第1局，假定比赛中不出现平局.

1)若两人之间共进行3局比赛，3局比赛须全部比完，赢满2局的人即获胜，请用树状图分析折颜最终获胜的概率；

2)若两人共进行7局比赛，7局比赛须全部比完，赢满4局的人即获胜，请直接写出折颜最终获胜的概率.

说明此题的初稿如下：小张和小钱两人进行围棋比赛，假如两人每局比赛输赢的机会相同，且小张已经赢得了第1局，两人之间共进行5局比赛，5局比赛须全部比完，赢满3局的人即获胜，请用树状图或列表分析小张最终获胜的概率.

初稿以围棋比赛为背景，主要考查利用枚举法(列表、画树状图)来计算概率，但有如下几个问题：首先，符合题意的树状图有4层，而考试中，一般不考查超过3层的树状图；其次，考生可能产生这样的疑虑：围棋比赛中是否需要考虑平局的情况；最后，题目略显单薄，缺乏新意.

回顾近几年的江苏省无锡市数学中考卷，笔者发现概率命题已经形成一些稳定的风格：背景多样，构思精巧，富有创意，在考查利用枚举法(列表、画树状图)来计算概率的同时，也经常会在第2)小题中设计一些创新题，需要学生理解情境，深入思考，灵活求解.

于是，笔者保留了围棋比赛的情境，在题干中加上“假定比赛中不出现平局”，使题目更加严谨.重新设计了两个小题：第1)小题考查学生利用两层的树状图计算概率；第2)小题要求学生考虑7局4胜的赛制下的获胜概率.显然，若学生仍利用树状图分析第2)小题，则会耗费大量的时间和精力，一不小心就会得到错误的结果.这就要求学生能对获胜的情况进行合理分类，并且明确：在等可能条件下，事件A发生的概率是事件A发生的结果数与所有可能发生的结果数之比.最后，将初稿中的人物改成了深受学生喜爱的影视人物，以增强试题的趣味性，缓解学生考试紧张的情绪.

2 思考感悟

回顾一模试卷的命制过程，笔者有几点感悟，与大家分享.

2.1 精选试题，应符合课标要求

现在的教辅资料丰富，网络技术发达，获得试题资源变得越来越容易，但题目质量参差不齐.因此，命题者需要仔细甄别，精选出其中的好题.一般来说，选题应主要来自教材习题、中考题、中考模拟题，以确保题目质量.选题必须符合《课程标准》的要求，贴近本地中考试题的命题特点.选题数量应比最终确定的试题数量多一些，以备结合考点统计表进行筛选.

2.2 深层改编，应体现诊断价值

选取好题进行改编是命题的常用手段.如果仅仅简单地改变原题中的数据、背景等，虽然确保了试题的命制方向不会出现大的偏差，但会造成试题陈旧、考查角度单一等问题，在一定程度上丧失了对知识技能掌握程度的诊断.因此，命题时应尽可能地深入改编，多角度、深层次地考查学生对知识技能的掌握程度，体现出一模考试的诊断功能.

2.3 注重导向，应彰显原创精神

试题若只是挑选或改编原题，则成了“拿来主义”，因此作为试卷亮点的原创题是必不可少的.事实上，原创题也是命题者价值取向的完整体现.命制原创题需要认真构思试题的教学导向，是导向重视某个核心概念的教学，还是导向形成建构主义教学观或是导向培养学生应用意识、创新意识等等.这对后续教师的教学、学生的学习都会产生重要的影响.

2.4 反复打磨，应追求简洁自然

从上文的命题过程可以看出，笔者经历了充分的思考，对试题进行了反复的打磨和优化.首先，命题者需对试卷反复审核，字斟句酌，以避免争议，杜绝科学性的错误；其次，试题的打磨应追求简洁明了，晓达通畅.本次一模卷共28题，但只有约1 800个字符，其简洁性可见一斑.章建跃教授曾指出：好的题目应该简洁好懂，自然生长.因此，在命制综合题时，还要思考如何使各个小题之间富于关联，自然生长，问题之间不能毫无联系，东拼西凑.

总之，命制好的试题，需要命题者平时注重积累，苦心经营，对试题精益求精，不断雕琢.最后，引用屈原《离骚》中的一句话与命题爱好者们共勉：路漫漫其修远兮，吾将上下而求索.

[1] 周伟扬.初中学业考数学试卷命制的着眼点——以2013年绍兴市初中学业考数学卷为例[J].中学教研(数学),2013(9):47-48.

2017-10-18

张 涛(1992-)，男，江苏泰州人，中学二级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)12-39-04