对一个常见数列不等式的探究与推广

●

(岳西中学,安徽 安庆 246600)

对一个常见数列不等式的探究与推广

●储百六

(岳西中学,安徽 安庆 246600)

文章通过对一个常见数列不等式的分析、证明、推广、寻根，指出一种解决与数列前n项积有关不等式的通用方法，该方法既能证明不等式，又能发现不等式.

不等式；前n项积估界；沃尔斯不等式

1 试题呈现

一天课间，一名学生来问笔者如下一道常见的数列不等式题:

例1求证：对一切正整数n，有

2 问题提出

该不等式曾多次在高考中出现过，证法很多，可以用数列单调性、数学归纳法、构造对偶式等等，难度也不大.再一次看到该问题时，不禁想到：

1)这个不等式从何而来？

3)可能得到一个类似的下界？

3 问题的探究与推广

命题1对一切正整数n，有

分析式(1)的证明不难，关键是如何得到，下面来探讨式(1)是如何得到的.

一方面，设待定参数λ使其满足

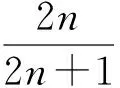
即

解得

另一方面，设参数μ使其满足

即

解得

证明从第二项开始放缩.一方面，由

可得

故对一切正整数n，有

故对一切正整数n,有

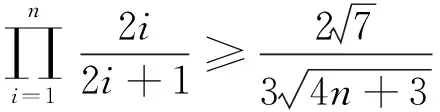
综上所述，对一切正整数n，有

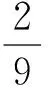
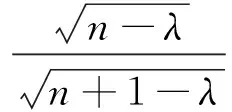
且当λ的取值越大，所得结果越强.特别地当λ=0时，即可得到例1的结论：

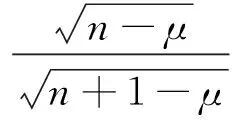
且当μ的取值越小，所得结果越强.

进一步，我们还可以将式(1)推广为：

命题2已知k≥1，则对一切正整数n，有

分析式(2)的证明不难，关键是如何得到，下面来说明式(2)是如何得到的.

一方面，设待定参数λ使其满足

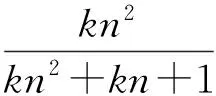
即

解得

另一方面，设参数μ使其满足

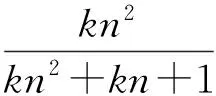
即

解得

证明方法同命题1，此处略.

注：当k=4时，式(2)即为式(1).

类比式(2)还可得到：

命题3已知k≥2，则对一切正整数n，有

(3)

分析式(3)的证明不难，关键是如何得到，下面来说明式(3)是如何得到的.

一方面，设待定参数λ使其满足

即

解得

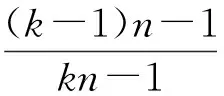
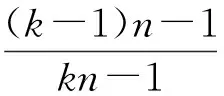
另一方面，设参数μ使其满足

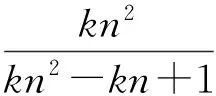
即

解得

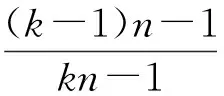
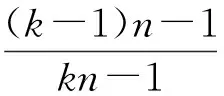
证明方法同命题1，此处略.

注：当k=4时，式(3)即为如下式(4).

例2对一切正整数n，有

式(4)为数学通报2 146号问题的加强.

4 总结与反思

读者可自行探究.

2)本文中待定参数λ，与列方程解应用题中的x有类似的作用，体现了方程思想在解决问题中的强大作用.

3)对于式(1)和式(4)的由来，笔者查阅一些资料认为，该问题应该来自沃尔斯公式的一个推导，结果为：

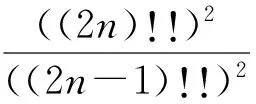
这里要用到定积分的知识，利用初等的方法不知可否做出，期待大家共同探讨.

[1] 单墫.我怎样解题[M].哈尔滨：哈尔滨工业大学，2013：24-26.

[2] 常庚哲,史济怀.数学分析教程[M].合肥：中国科学技术大学，2012:309.

2017-10-14

储百六(1984-)，男，安徽岳西人，中学一级教师.研究方向：数学教育.

O122.3

A

1003-6407(2017)12-23-03